1 000 Divided By 5
saludintensiva
Sep 11, 2025 · 6 min read
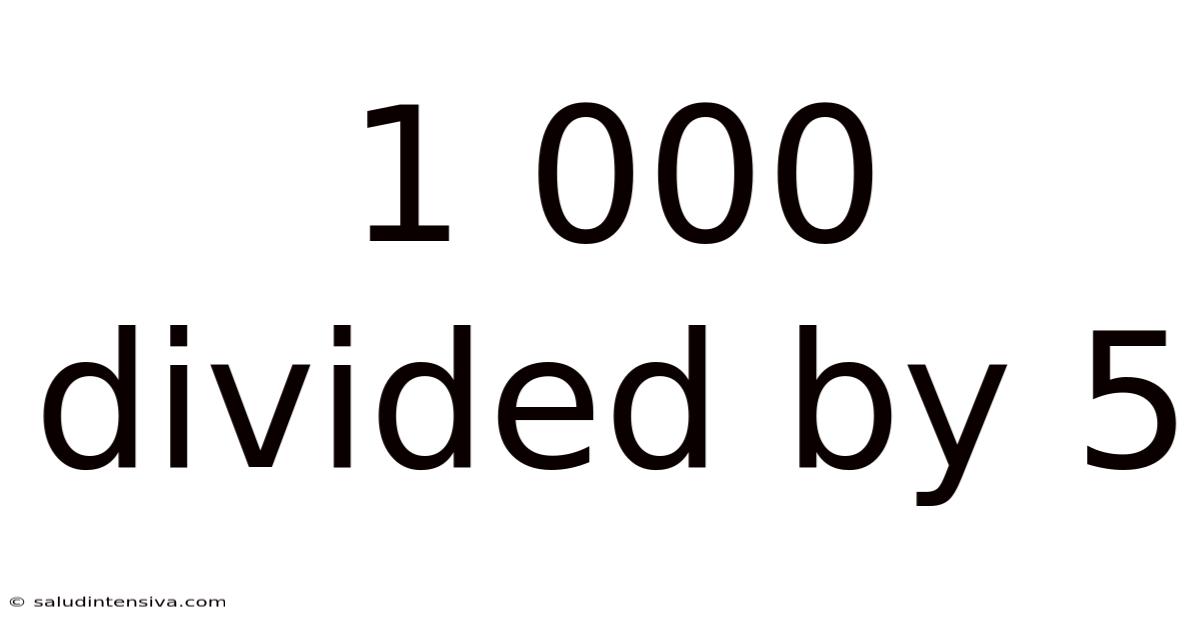
Table of Contents
1,000 Divided by 5: A Deep Dive into Division and its Applications
Dividing 1,000 by 5 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly basic calculation provides a fantastic springboard to explore fundamental concepts in mathematics, delve into various methods of solving division problems, and uncover its practical applications in everyday life and more complex fields like engineering and finance. This article will not only show you how to solve 1,000 ÷ 5 but also illuminate the underlying principles and broaden your understanding of division itself.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the equation 1,000 ÷ 5, we're asking: "How many times does 5 go into 1,000?" The answer, as we'll explore in detail, is 200. But understanding why 200 is the answer is crucial to grasping the broader concept of division. This understanding extends beyond simple calculations and forms the basis for more advanced mathematical concepts.
Methods for Solving 1,000 ÷ 5
Several methods can be employed to solve 1,000 divided by 5. Let's explore a few:
-
Long Division: This is a classic method taught in schools. It involves a step-by-step process of dividing the dividend (1,000) by the divisor (5).
5 | 1000 -5 --- 50 -50 --- 00 -00 --- 0We start by dividing 5 into 10 (the first two digits of 1000), which equals 2. We write the 2 above the 0 in 1000. Then, we multiply 2 by 5 (getting 10), subtract it from 10, and bring down the next digit (0). We repeat this process until we have no more digits to bring down. The final answer is 200.
-
Short Division: A more concise version of long division, suitable for simpler problems. It's essentially the same process but performed mentally, often using smaller intermediary steps. For 1000 ÷ 5, we can quickly observe that 10 ÷ 5 = 2. Since 1000 is 100 times larger than 10, the answer is 200.
-
Repeated Subtraction: This method involves repeatedly subtracting the divisor (5) from the dividend (1,000) until you reach zero. The number of times you subtract is the quotient (the answer). While effective for smaller numbers, it's less practical for large numbers like 1,000.
-
Multiplication: Since division is the inverse of multiplication, we can find the answer by asking: "What number multiplied by 5 equals 1,000?" The answer, again, is 200. This method utilizes the relationship between multiplication and division and reinforces their inverse nature.
The Scientific Explanation: Understanding Quotients and Remainders
In the context of 1,000 ÷ 5, we have a whole number dividend (1,000) and a whole number divisor (5). The result, 200, is a whole number quotient. This means the divisor divides the dividend evenly, leaving no remainder. A remainder occurs when the divisor doesn't divide the dividend perfectly. For example, if we were dividing 1,001 by 5, the quotient would be 200, and the remainder would be 1 (because 200 x 5 = 1000, leaving 1).
The concept of remainders is crucial in many applications, particularly in situations involving discrete quantities that cannot be easily divided into fractions. Imagine sharing 1001 apples among 5 people; each person gets 200 apples, and one apple is left over.
Real-World Applications of Division: Beyond the Classroom
The seemingly simple calculation of 1,000 ÷ 5 has numerous real-world applications:
-
Sharing Equally: Dividing resources equally among a group of people. For instance, distributing 1,000 candies among 5 friends.
-
Unit Conversions: Converting units of measurement. If you have 1,000 centimeters and need to convert it to meters (100 centimeters per meter), you divide 1,000 by 100.
-
Averaging: Calculating the average of a set of numbers. If you have 5 scores totaling 1,000 points, the average score is 200.
-
Finance: Calculating per-unit costs. If you bought 5 items for $1,000, each item cost $200.
-
Engineering: Determining the number of components needed for a project. If a project requires 5 identical parts, and you have 1,000 units in stock, you can create 200 complete units.
-
Data Analysis: Analyzing large datasets. Imagine a dataset with 1,000 entries that you need to group into 5 categories.
-
Recipe Scaling: Scaling up or down a recipe. If a recipe calls for 5 grams of an ingredient and you need 1,000 grams, you need to multiply the recipe by 200.
Exploring Further: Division with Decimals and Fractions
While 1,000 ÷ 5 results in a whole number, division can also involve decimals and fractions. Understanding how to handle these scenarios is crucial for a more complete grasp of division.
-
Dividing by decimals: If we were to divide 1,000 by 0.5, we'd get 2,000. This is because 0.5 is equivalent to ½, and dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Dividing by fractions: Dividing by a fraction (e.g., 1,000 ÷ ⅛) involves multiplying by its reciprocal (8/1 or 8). The result would be 8,000. This demonstrates the interplay between division and fractions and reinforces the concept of reciprocals.
Frequently Asked Questions (FAQs)
-
What if I have a remainder after dividing 1,000 by a different number? If you divide 1,000 by a number that doesn't divide it evenly, you'll have a remainder. This remainder represents the portion of the dividend that wasn't fully divided by the divisor. For example, 1001 ÷ 5 = 200 with a remainder of 1.
-
How do I check my answer when dividing? You can always check your division answer by multiplying the quotient by the divisor. If the result equals the dividend, your answer is correct. For instance, 200 x 5 = 1,000, confirming that 200 is the correct quotient for 1,000 ÷ 5.
-
What are some common mistakes people make when dividing? Common mistakes include errors in place value during long division, misplacing decimal points when dividing with decimals, and forgetting to account for remainders.
Conclusion: The Enduring Importance of Division
The seemingly simple problem of 1,000 divided by 5 unlocks a wealth of mathematical knowledge and practical applications. By understanding the various methods for solving this type of problem, comprehending the concepts of quotients and remainders, and recognizing its relevance in everyday scenarios, you've gained a deeper understanding of division and its significant role in mathematics and beyond. This fundamental arithmetic operation is a cornerstone for more complex mathematical concepts and plays a vital part in countless real-world applications, from everyday tasks to specialized fields. Mastering division is not just about finding the answer; it’s about developing a crucial skill that empowers problem-solving and critical thinking.
Latest Posts
Latest Posts
-
4 To The 2 Power
Sep 11, 2025
-
12 16 In Simplest Form
Sep 11, 2025
-
Greatest Common Factor For 48
Sep 11, 2025
-
Lcm Of 15 And 10
Sep 11, 2025
-
14 15 As A Decimal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 000 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.