1 025 Divided By 25
saludintensiva
Sep 21, 2025 · 7 min read
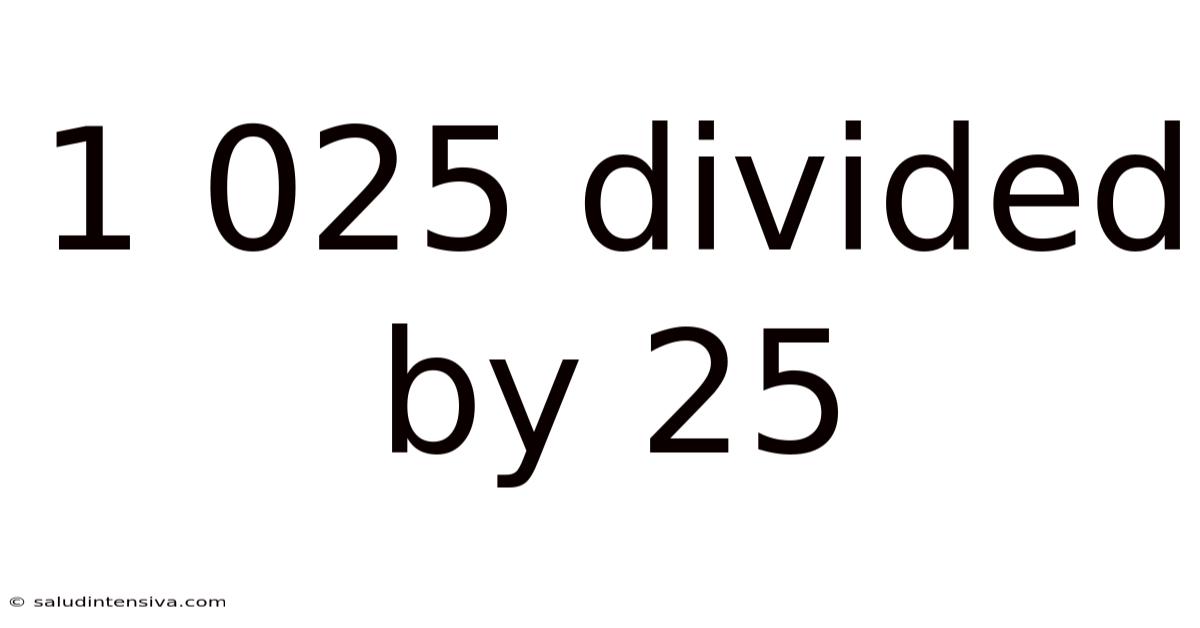
Table of Contents
Unraveling the Mystery: 1025 Divided by 25
Dividing numbers might seem like a simple arithmetic operation, something we learn in elementary school and then promptly forget. But the act of dividing 1025 by 25, seemingly straightforward, offers a fascinating glimpse into the underlying principles of mathematics and provides a springboard for exploring more complex concepts. This article will not only solve the problem but delve deeper into the methods, reasoning, and applications of division, making it accessible and engaging for all readers. We will uncover multiple approaches to solving this problem, illustrating the beauty and versatility of mathematical tools. Whether you're a student refreshing your skills or an adult curious about the deeper workings of arithmetic, this comprehensive exploration promises to be both informative and rewarding.
Understanding Division: A Fundamental Concept
Division, at its core, is the process of splitting a quantity into equal parts. When we divide 1025 by 25, we're essentially asking: "How many times does 25 fit into 1025?" This question has practical applications across various fields, from splitting a bill equally among friends to calculating the number of tiles needed to cover a floor. The answer we obtain, called the quotient, represents the number of equal parts, while any remaining amount, called the remainder, signifies the portion that cannot be perfectly divided.
The standard notation for division is 1025 ÷ 25 or 1025/25. Both notations represent the same operation.
Method 1: Long Division – A Classic Approach
Long division is a time-tested method that systematically breaks down the division process into smaller, manageable steps. It's particularly useful for larger numbers and allows for a clear understanding of each step involved. Let's walk through the process of dividing 1025 by 25 using long division:
-
Set up the problem: Write 1025 inside the long division symbol (⟌) and 25 outside.
-
Divide the hundreds: How many times does 25 go into 10? It doesn't go in at all, so we move to the tens place. How many times does 25 go into 102? It goes in 4 times (4 x 25 = 100). Write the 4 above the 2 in 1025.
-
Multiply and subtract: Multiply the 4 by 25 (4 x 25 = 100) and write the result below 102. Subtract 100 from 102, leaving a remainder of 2.
-
Bring down the next digit: Bring down the 5 from 1025, creating the number 25.
-
Divide the remaining digits: How many times does 25 go into 25? It goes in exactly once (1 x 25 = 25). Write the 1 above the 5 in 1025.
-
Multiply and subtract: Multiply 1 by 25 (1 x 25 = 25) and subtract it from 25. The remainder is 0.
Therefore, 1025 ÷ 25 = 41.
Method 2: Using Multiplication and Estimation – A Faster Approach
Instead of long division, we can use our knowledge of multiplication tables and estimation to solve this problem more efficiently. We know that 25 x 40 = 1000. This is close to 1025. The difference is 25 (1025 - 1000 = 25). Since 25 x 1 = 25, we add 1 to our initial estimate of 40, resulting in 41. Therefore, 1025 ÷ 25 = 41. This method demonstrates the power of mental arithmetic and estimation in solving division problems quickly.
Method 3: Breaking Down the Numbers – A Conceptual Approach
We can simplify the problem by breaking down the numbers into smaller, more manageable units. Since 1025 is a multiple of 25 (1025 = 25 x 41), we can see that 25 will go into 1025 exactly 41 times. The beauty of this approach lies in revealing the inherent relationship between the numbers, making the division operation less of an algorithmic exercise and more of a discovery. This emphasizes understanding the fundamental properties of numbers.
Method 4: Using Fractions – Connecting Division to Fractions
Division can also be expressed as a fraction. The expression 1025 ÷ 25 is equivalent to the fraction 1025/25. Simplifying this fraction involves finding the greatest common divisor (GCD) of 1025 and 25. The GCD of 1025 and 25 is 25. Dividing both the numerator and denominator by 25, we get:
1025/25 = (1025 ÷ 25) / (25 ÷ 25) = 41/1 = 41
This approach connects division to the fundamental concept of fractions and demonstrates the interconnectedness of mathematical operations.
The Significance of the Quotient and Remainder
In the case of 1025 divided by 25, we obtained a quotient of 41 and a remainder of 0. The quotient indicates the number of times 25 fits perfectly into 1025. A remainder of 0 signifies an exact division, meaning that 1025 is a multiple of 25. Had there been a non-zero remainder, it would have represented the portion of 1025 that remained after dividing it into equal parts of 25.
Real-World Applications of Division
The simple act of dividing 1025 by 25 has far-reaching implications in numerous real-world scenarios:
- Resource allocation: Dividing resources equally among individuals or groups. For example, dividing 1025 candies among 25 children.
- Unit conversion: Converting units of measurement. For example, converting 1025 centimeters into meters (1 meter = 100 centimeters).
- Financial calculations: Calculating unit cost, profit margins, or splitting bills.
- Engineering and design: Determining the number of components needed in a project.
- Data analysis: Calculating averages, ratios, or proportions.
Extending the Learning: Exploring More Complex Divisions
While 1025 divided by 25 provides a solid foundation, we can extend our learning to more complex division problems. Consider scenarios where the divisor is not a factor of the dividend, resulting in a non-zero remainder. This exploration will deepen your understanding of division and its applications in various mathematical contexts. Understanding how to handle remainders is crucial in many practical situations. For instance, if you were dividing 1026 by 25, the quotient would be 41, and the remainder would be 1. This remainder would represent one item that cannot be included in the equal groups.
Frequently Asked Questions (FAQs)
Q: What is the most efficient method to divide 1025 by 25?
A: The most efficient method depends on individual preference and mathematical skills. For quick mental calculations, the estimation method is often fastest. For a clear step-by-step approach, long division is preferred. Using fractions simplifies the concept but might require more steps.
Q: What if the numbers were larger? Would the same methods still apply?
A: Yes, the methods discussed (long division, estimation, using fractions) can be applied to larger numbers as well. However, long division might become more time-consuming, making estimation and understanding numerical relationships even more valuable.
Q: What is the importance of understanding remainders in division?
A: Understanding remainders is crucial because it provides information about the portion that cannot be perfectly divided into equal groups. This information is essential in many real-world applications, such as determining how many extra items are needed or how to handle incomplete groups.
Q: How does this relate to other mathematical concepts?
A: Division is fundamentally linked to multiplication, subtraction, and fractions. It's also closely related to concepts such as factors, multiples, and greatest common divisors (GCD). A strong understanding of division is critical for mastering more advanced mathematical concepts, including algebra and calculus.
Conclusion: A Deeper Appreciation for Division
The seemingly simple task of dividing 1025 by 25 provides a gateway to a deeper understanding of fundamental mathematical principles. Through long division, estimation, simplification through fractions, and exploring real-world applications, we've not only solved the problem but also gained a richer appreciation for the elegance and versatility of division. This exploration extends beyond the mere calculation of a numerical answer, revealing the interconnectedness of mathematical concepts and their practical applications in various aspects of life. Understanding the nuances of division empowers us to approach more complex problems with confidence and creativity, fostering a lifelong appreciation for the power of mathematics.
Latest Posts
Latest Posts
-
How Much Time Until 12 30
Sep 21, 2025
-
X 2 10x 25 Factor
Sep 21, 2025
-
Decrease 9 3 8 By 4 37
Sep 21, 2025
-
4 To 1 Ratio Ladder
Sep 21, 2025
-
What Is A 46 50 Grade
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 025 Divided By 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.