1 1 2 2 3
saludintensiva
Sep 17, 2025 · 6 min read
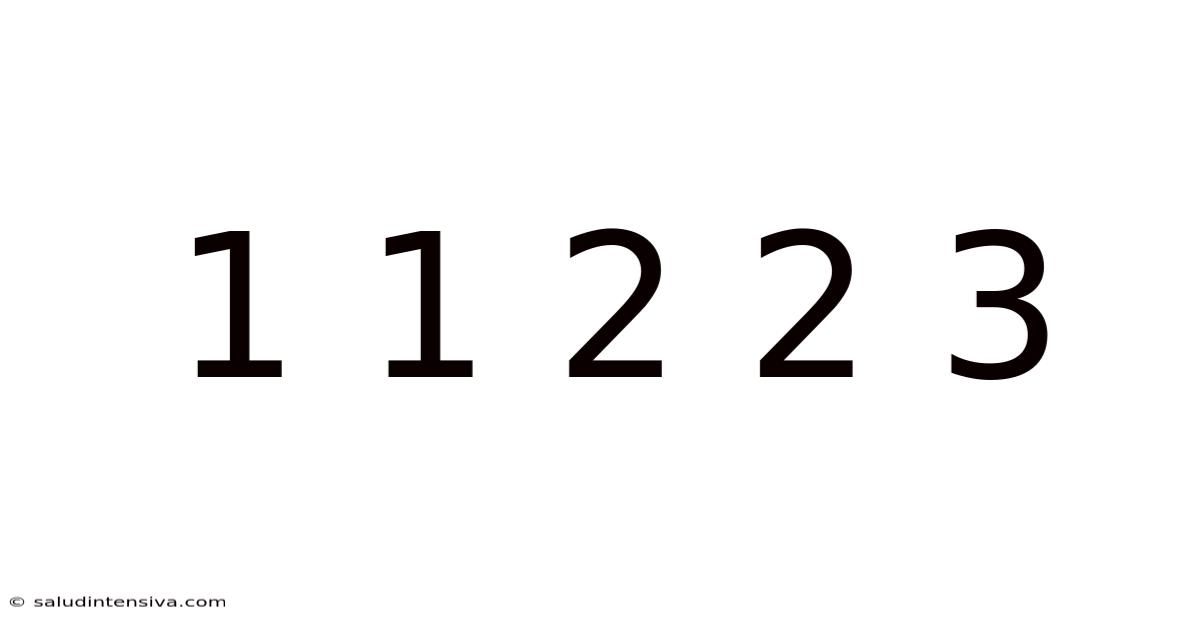
Table of Contents
Unraveling the Mystery of 1 1 2 2 3: Exploring Sequences, Patterns, and Mathematical Thinking
This article delves into the seemingly simple sequence "1 1 2 2 3," exploring its potential interpretations, underlying mathematical concepts, and the broader implications for understanding patterns and sequences. We'll examine different perspectives, from basic number patterns to more complex mathematical structures, ultimately highlighting the power of observation and logical deduction in problem-solving. This exploration is relevant for students learning about sequences, pattern recognition, and the foundations of mathematical thinking.
Introduction: The Allure of Simple Sequences
The sequence "1 1 2 2 3" may appear deceptively simple at first glance. However, its very simplicity invites us to explore the possibilities of what comes next, and more importantly, why. Understanding the underlying rules governing such sequences is fundamental to mathematics, allowing us to predict future terms, model real-world phenomena, and develop our problem-solving skills. This seemingly straightforward sequence can act as a gateway to understanding more complex mathematical concepts.
Identifying Potential Patterns: A Multifaceted Approach
There's no single "correct" answer to what comes next in the sequence "1 1 2 2 3". The beauty lies in the multiple interpretations and the reasoning behind them. Let's explore several possible approaches:
1. The Simplest Pattern: Repetition and Increment
The most straightforward approach is to identify a repeating pattern and a subsequent increment. We see a repetition of each number followed by a sequential increase. Following this pattern, the next numbers would be 3 4 5 5... and so on. This pattern is easily understandable and demonstrates a basic understanding of sequence construction.
2. Introducing a Recursive Pattern
We can also view this as a recursive sequence where the next number depends on the previous ones. One potential recursive rule could be:
- The first number is 1.
- The second number is 1.
- Every subsequent number is the sum of the two preceding numbers minus the second-to-last number. (This is a simplified illustrative example, not a universally applicable rule).
This approach introduces a more complex relationship between the terms, moving beyond simple repetition to a more dynamic generation of the sequence. Further investigation could lead to exploring different recursive rules and evaluating their predictive power.
3. A Look at Look-and-Say Sequences
While less likely for this specific sequence, we can consider the possibility of a "look-and-say" sequence. This type of sequence involves describing the previous sequence numerically. For example, "1" becomes "11" (one 1), "11" becomes "21" (two 1s), "21" becomes "1211" (one 2, one 1), and so on. This sequence, however, doesn't directly fit "1 1 2 2 3," but understanding the concept of look-and-say sequences broadens our understanding of pattern recognition.
4. Exploring Prime Numbers and Factorization
Although less obvious, we can explore whether prime numbers or factorization plays a role. While 1 isn't considered prime, the inclusion of 2 and 3, the first two prime numbers, could suggest a link. However, this approach requires more numbers in the sequence to verify such a hypothesis.
The Significance of Mathematical Induction and Proof
Once we've identified a potential pattern, the next step is to validate it using mathematical induction or other forms of proof. Mathematical induction is a powerful technique for proving that a statement is true for all natural numbers. However, proving a statement about this specific sequence using induction would require a clearly defined generating rule. Without a rigorously defined pattern, applying mathematical induction would be inappropriate.
For example, if we hypothesize the "repetition and increment" pattern, we'd attempt to prove it inductively. The base case would be verifying the initial terms of the sequence. The inductive step would then involve showing that if the pattern holds for the nth term, it must also hold for the *(n+1)*th term. This would require a formal mathematical expression to represent the pattern.
The Role of Context: Data Analysis and Real-World Applications
The interpretation of the sequence "1 1 2 2 3" could also depend on the context. If this sequence originated from a data set, such as measurements from an experiment or observations from a natural phenomenon, its meaning would be strongly tied to that context. Analyzing its statistical properties (e.g., mean, variance, etc.) within the broader context would be crucial in that case. This could help us determine whether it represents a random occurrence or a meaningful trend within the larger dataset.
Frequently Asked Questions (FAQs)
Q: Is there a single correct answer to the sequence?
A: No, there isn't a single definitive answer. The value lies in exploring various potential patterns and reasoning behind them, not necessarily finding the correct continuation.
Q: How can I improve my pattern recognition skills?
A: Practice is key! Work through various sequence problems, starting with simple ones and gradually increasing complexity. Consider exploring resources such as mathematical textbooks, online courses, and puzzle books.
Q: What are some other types of sequences I can explore?
A: There's a vast world of sequences to explore! Fibonacci sequences, geometric sequences, arithmetic sequences, and many more complex types each have their unique characteristics and applications.
Q: What are the real-world applications of understanding sequences?
A: Understanding sequences has numerous applications in various fields: * Computer Science: Algorithm design, data structures. * Finance: Predictive modeling, stock market analysis. * Physics: Modeling physical phenomena, analyzing data from experiments. * Biology: Analyzing growth patterns, population dynamics.
Conclusion: The Power of Mathematical Exploration
The apparently simple sequence "1 1 2 2 3" serves as a compelling example of how seemingly straightforward problems can lead to insightful explorations of mathematical concepts. By examining various potential patterns, applying logical reasoning, and considering different perspectives, we can develop our problem-solving abilities and deepen our understanding of sequences, pattern recognition, and mathematical thinking. The process of exploration is just as valuable as arriving at a specific answer, emphasizing the importance of critical thinking and creative problem-solving in mathematics. The lack of a single definitive answer allows for a rich learning experience, promoting deeper engagement and reinforcing fundamental mathematical principles. This exploration encourages flexibility in thought and highlights the multi-faceted nature of mathematical problem solving. The journey of unraveling the mystery of this sequence demonstrates the potential of even seemingly simple problems to unlock a broader understanding of mathematical concepts and the power of logical reasoning. By exploring different patterns and methods of analysis, we are not only extending our knowledge of sequences, but also developing crucial critical thinking and problem-solving skills applicable far beyond the realm of mathematics.
Latest Posts
Latest Posts
-
25 Weeks Ago From Today
Sep 17, 2025
-
150 Million In Scientific Notation
Sep 17, 2025
-
2 3 X 1 4
Sep 17, 2025
-
2 3 8 In Decimal Form
Sep 17, 2025
-
Greatest Common Factor Of 38
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.