1 1 2 3 5
saludintensiva
Sep 22, 2025 · 6 min read
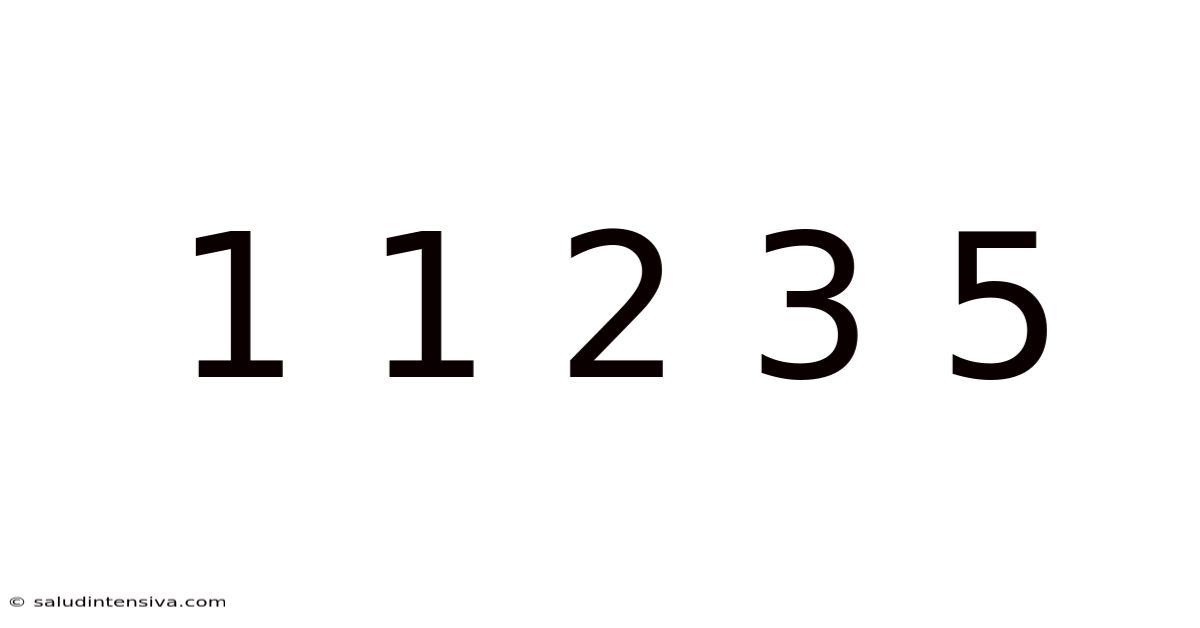
Table of Contents
Decoding the Magic: Exploring the Fibonacci Sequence and its Applications
The sequence 1, 1, 2, 3, 5... might seem unremarkable at first glance. However, this seemingly simple pattern, known as the Fibonacci sequence, is a cornerstone of mathematics with surprising applications across various fields, from nature's intricate designs to complex algorithms in computer science. This article delves deep into the Fibonacci sequence, exploring its origins, mathematical properties, and its fascinating presence in the world around us.
Introduction: Unveiling the Fibonacci Sequence
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. Therefore, the sequence begins: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. While often represented starting with 1, 1, understanding the inclusion of 0 provides a more complete mathematical picture. This seemingly simple rule generates a sequence with profound mathematical properties and astonishing connections to the natural world. This exploration will cover the history of the sequence, its mathematical intricacies, and its far-reaching applications.
Historical Context: A Journey Through Time
While often attributed to Leonardo Pisano, better known as Fibonacci (c. 1170 – c. 1250), the sequence was known centuries earlier in Indian mathematics. However, Fibonacci's 1202 book, Liber Abaci, introduced the sequence to the Western world, significantly impacting its development and dissemination. The problem presented in Liber Abaci involved the growth of a rabbit population under idealized conditions, leading to the generation of this iconic sequence. This problem, while seemingly simple, elegantly demonstrated the recursive nature of the sequence and laid the foundation for its future study. The impact of Fibonacci’s work cannot be overstated; his book was instrumental in the spread of Hindu-Arabic numerals across Europe, replacing the cumbersome Roman numeral system.
Mathematical Properties: Beyond the Surface
The Fibonacci sequence is more than just a simple pattern; it boasts a rich tapestry of mathematical properties. Let's explore some key aspects:
-
Recursive Definition: As mentioned earlier, the most fundamental property is its recursive definition: F(n) = F(n-1) + F(n-2), where F(n) represents the nth Fibonacci number. This simple rule allows for the generation of the entire sequence.
-
The Golden Ratio (Φ): A remarkable property of the Fibonacci sequence is its connection to the golden ratio, approximately 1.618. As the sequence progresses, the ratio of consecutive Fibonacci numbers (e.g., 5/3, 8/5, 13/8) increasingly approaches the golden ratio. This relationship forms the basis for many of the sequence's applications in art, architecture, and nature.
-
Closed-Form Expression (Binet's Formula): While the recursive definition is elegant, it's not the most efficient way to calculate larger Fibonacci numbers. Binet's formula provides a direct method:
F(n) = [(1 + √5)^n - (1 - √5)^n] / (2^n √5)
This formula, though appearing complex, allows for the direct calculation of any Fibonacci number without needing to calculate all preceding numbers.
-
Generating Functions: The Fibonacci sequence can also be represented using generating functions, which are power series whose coefficients correspond to the terms of the sequence. This powerful tool allows for the application of calculus to analyze the properties of the sequence.
The Fibonacci Sequence in Nature: A Tapestry of Patterns
The most captivating aspect of the Fibonacci sequence is its ubiquitous presence in the natural world. This seemingly mathematical abstraction finds tangible expression in various forms:
-
Phyllotaxis (Arrangement of Leaves): The arrangement of leaves on a stem, petals on a flower, and seeds in a sunflower head often follows Fibonacci numbers. This optimized arrangement ensures efficient sunlight capture and minimal overlap.
-
Flower Petals: Many flowers exhibit a number of petals that corresponds to a Fibonacci number (e.g., lilies have three petals, buttercups have five, daisies often have 34 or 55).
-
Pine Cones and Pineapples: The spiral patterns on pine cones and the scales on pineapples are also governed by Fibonacci numbers, reflecting an efficient packing arrangement.
-
Seashells: The spiral structure of many seashells, such as the nautilus shell, closely approximates a logarithmic spiral, a curve intimately related to the golden ratio and the Fibonacci sequence.
-
Branching Patterns in Trees: The branching patterns of trees, with their main trunk splitting into branches, then smaller branches, and so on, often exhibit Fibonacci-like proportions.
Applications Beyond Nature: Expanding the Horizons
The Fibonacci sequence's influence extends far beyond the natural world. Its mathematical properties find applications in diverse fields:
-
Computer Science: Fibonacci numbers are used in algorithms and data structures, such as Fibonacci heaps and Fibonacci search. These algorithms offer efficient solutions to various computational problems.
-
Art and Architecture: The golden ratio, closely related to the Fibonacci sequence, has been used for centuries in art and architecture to create aesthetically pleasing proportions. The Parthenon in Greece, for instance, displays proportions related to the golden ratio.
-
Financial Markets: Some believe that Fibonacci numbers and the golden ratio can be used to predict market trends, although this application is debated among financial experts.
-
Music: The Fibonacci sequence and the golden ratio appear in musical compositions, influencing aspects such as the placement of musical phrases and the creation of harmonies.
Frequently Asked Questions (FAQ)
-
Is the Fibonacci sequence infinite? Yes, the Fibonacci sequence is an infinite sequence, meaning it continues indefinitely.
-
Are all spiral patterns Fibonacci spirals? While many natural spirals approximate Fibonacci spirals, not all spirals are strictly Fibonacci. Some spirals may follow other mathematical patterns.
-
How is the Golden Ratio related to the Fibonacci Sequence? The ratio of consecutive Fibonacci numbers approaches the Golden Ratio as the sequence progresses. This relationship is a fundamental aspect of the Fibonacci sequence's beauty and relevance.
-
Are there any limitations to using the Fibonacci sequence in predictions (e.g., financial markets)? Using the Fibonacci sequence for prediction, particularly in financial markets, is not scientifically proven and is considered highly speculative. Many factors influence market behavior beyond simple mathematical patterns.
Conclusion: A Legacy of Beauty and Utility
The Fibonacci sequence, a simple pattern born from a seemingly simple problem, has blossomed into a rich area of mathematical exploration with profound implications across diverse fields. Its presence in nature showcases the elegance and efficiency of natural designs, while its applications in science and art highlight its versatility and enduring relevance. From the intricate spirals of seashells to the branching patterns of trees, and from the algorithms of computer science to the aesthetic principles of art, the Fibonacci sequence continues to fascinate and inspire, proving that even the simplest mathematical concepts can hold remarkable power and beauty. The ongoing study of this sequence continues to reveal new facets and potential applications, underscoring its enduring legacy as one of the most captivating and influential mathematical concepts of all time. The exploration of the Fibonacci sequence not only deepens our mathematical understanding but also provides a lens through which we can appreciate the intricate beauty and underlying order found throughout the natural world and the creations of humankind. Its influence continues to shape our understanding of patterns, proportions, and the elegant interplay between mathematics and the world around us.
Latest Posts
Latest Posts
-
What Is 2200 In Time
Sep 22, 2025
-
Mixed Fraction On Number Line
Sep 22, 2025
-
30 Days From February 28
Sep 22, 2025
-
Concrete Patio Per Square Foot
Sep 22, 2025
-
4 Digit Number Guessing Game
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.