1 1 2 X 2
saludintensiva
Sep 21, 2025 · 5 min read
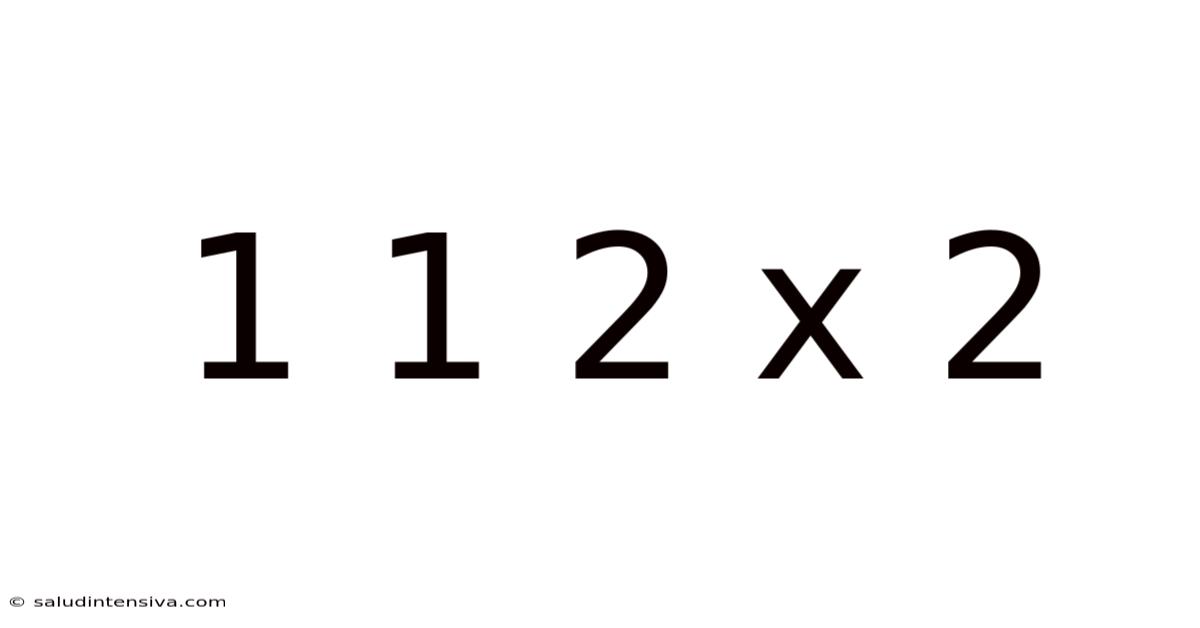
Table of Contents
Decoding 1 1 2 x 2: Exploring Patterns, Puzzles, and the Power of Simple Mathematics
The seemingly simple expression "1 1 2 x 2" might initially appear trivial, but it opens a fascinating doorway into the world of mathematical patterns, logic puzzles, and the surprising depth hidden within elementary arithmetic. This article delves into the multiple interpretations of this expression, exploring its potential solutions, the underlying principles involved, and the broader mathematical concepts it touches upon. We’ll unravel its mysteries, discuss possible ambiguities, and reveal how seemingly simple sequences can lead to complex and rewarding explorations.
Understanding the Ambiguity: Multiple Interpretations
The core challenge with "1 1 2 x 2" lies in its ambiguity. The lack of explicit operators between the numbers allows for several interpretations, highlighting the critical importance of precise mathematical notation. Let's examine some of the possibilities:
-
Interpretation 1: Concatenation and Multiplication: One possible reading interprets the initial "1 1 2" as the concatenation of digits, forming the number 112. The "x 2" then represents simple multiplication. Therefore, the solution would be 112 x 2 = 224. This interpretation relies on understanding the implicit concatenation operation.
-
Interpretation 2: Sequential Operations: Another interpretation suggests a sequence of operations. We could interpret this as (1 + 1) + 2 x 2. Following the order of operations (PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), we first perform the multiplication: 2 x 2 = 4. Then we add: (1 + 1) + 4 = 6. This interpretation requires a specific order of operations to be applied.
-
Interpretation 3: Pattern Recognition: This approach focuses less on strict arithmetic and more on identifying a potential underlying pattern. Let's analyze the initial sequence "1 1 2". Could this be the start of a recursive or iterative sequence? If so, what is the rule governing the sequence? We might look for a pattern, but this requires us to extend the sequence and test various generating rules. For instance, it could be argued (though not definitively) that the sequence is based on addition, with the next term being the sum of the previous two: 1 + 1 = 2. This doesn't fully explain the presence of "x 2," however.
Exploring Number Sequences and Pattern Recognition
The ambiguity highlights the power of pattern recognition in mathematics. Number sequences form a cornerstone of many mathematical disciplines. Understanding patterns helps us predict future terms, create mathematical models, and uncover hidden relationships.
Let's consider some common number sequence patterns:
- Arithmetic Sequences: These sequences have a constant difference between consecutive terms. For example, 2, 5, 8, 11… (common difference of 3).
- Geometric Sequences: These sequences have a constant ratio between consecutive terms. For example, 3, 6, 12, 24… (common ratio of 2).
- Fibonacci Sequence: This famous sequence begins with 0 and 1, and each subsequent term is the sum of the two preceding terms: 0, 1, 1, 2, 3, 5, 8…
- Recursive Sequences: These sequences are defined by a recursive formula, where the next term is a function of previous terms.
Determining whether "1 1 2" is part of a larger sequence requires careful analysis and consideration of various mathematical functions. The lack of additional data prevents a definitive answer. Further terms would be needed to discern the underlying pattern, if one exists.
The Role of Mathematical Notation and Precision
The ambiguity of "1 1 2 x 2" underscores the critical importance of precise mathematical notation. In mathematics, precise language and unambiguous symbols are essential for clear communication and avoiding misinterpretations. Parentheses, brackets, and clearly defined operators are indispensable for avoiding multiple possible interpretations.
For instance, writing (1 + 1) + (2 x 2) eliminates the ambiguity and clearly indicates the order of operations. Similarly, 112 x 2 leaves no room for doubt regarding concatenation and multiplication.
Expanding on Mathematical Operations
This expression touches upon fundamental mathematical operations:
- Addition (+): Combining quantities.
- Multiplication (x): Repeated addition.
- Concatenation: Combining numbers or strings by placing them side by side.
Understanding these operations is crucial for solving a wide range of mathematical problems. It's important to note that the order in which these operations are performed is dictated by the rules of precedence (PEMDAS/BODMAS).
Practical Applications and Problem-Solving Strategies
While "1 1 2 x 2" might seem like a simple, abstract puzzle, the principles it illustrates have practical applications in various fields:
- Programming: Understanding order of operations is crucial in programming, where the correct sequence of calculations determines the program's outcome.
- Data Analysis: Identifying patterns in data sets is vital in fields like statistics and machine learning.
- Engineering: Mathematical models and equations are used extensively in engineering to design and analyze systems.
Solving this puzzle, or puzzles like it, hones critical thinking skills, problem-solving abilities, and the ability to approach problems with creativity and logic.
Frequently Asked Questions (FAQ)
-
Q: What is the definitive answer to 1 1 2 x 2?
- A: There's no single definitive answer without clarifying the intended operations. The expression is inherently ambiguous.
-
Q: How can I avoid ambiguity in mathematical expressions?
- A: Use parentheses, brackets, and clear operators to define the order of operations and prevent multiple interpretations.
-
Q: What are some other examples of ambiguous mathematical expressions?
- A: Expressions like 6 ÷ 2(1 + 2) are notorious for generating conflicting answers due to the order of operations debate. The use of implicit multiplication can lead to confusion.
-
Q: What are some resources for improving my mathematical skills?
- A: Textbooks, online courses, and educational websites offer valuable resources for learning more about various mathematical concepts.
Conclusion: The Beauty of Mathematical Exploration
The deceptively simple expression "1 1 2 x 2" has led us on a journey that explores the intricacies of mathematical notation, the importance of precise language, and the power of pattern recognition. While there's no single "right" answer without further context, the exploration itself provides valuable insights into fundamental mathematical principles and problem-solving strategies. This exercise highlights that even seemingly simple mathematical expressions can reveal hidden depths and encourage us to think critically and creatively about numerical relationships. The beauty lies not only in finding a solution but also in the process of understanding and appreciating the underlying mathematical structures. The ambiguity encourages a more profound engagement with the fundamentals of arithmetic and the crucial role of clarity in mathematical communication. The exploration of patterns and sequences expands the scope beyond a simple calculation and introduces broader mathematical concepts that are vital in various fields.
Latest Posts
Latest Posts
-
Ratio Word Problems 7th Grade
Sep 22, 2025
-
Business Days In April 2024
Sep 22, 2025
-
10 Trillion In Scientific Notation
Sep 22, 2025
-
40 Ft Container Cubic Meters
Sep 22, 2025
-
Square Root Of 1 10
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.