1 1/3 In Simplest Form
saludintensiva
Sep 18, 2025 · 5 min read
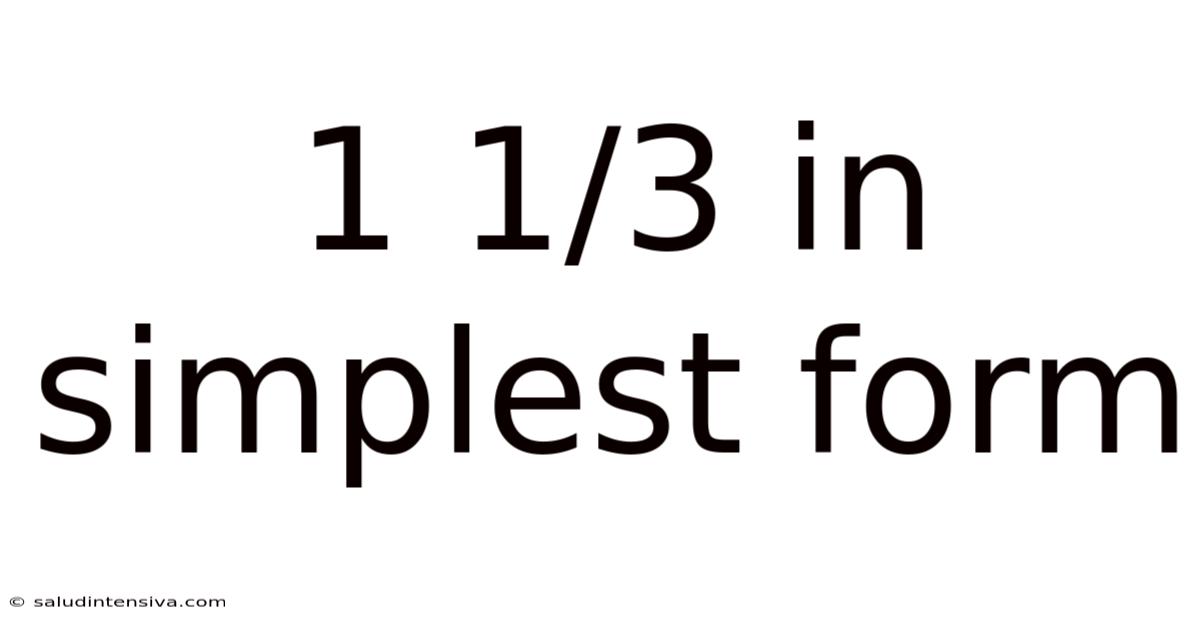
Table of Contents
Understanding Fractions: Simplifying 1 1/3 to its Simplest Form
Fractions are a fundamental part of mathematics, representing parts of a whole. Understanding how to manipulate and simplify fractions is crucial for success in various mathematical fields, from basic arithmetic to advanced calculus. This article will delve into the process of simplifying mixed numbers, specifically focusing on how to express the mixed number 1 1/3 in its simplest form. We'll explore the underlying concepts, provide a step-by-step guide, and address common questions about simplifying fractions.
Understanding Mixed Numbers and Improper Fractions
Before we simplify 1 1/3, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 1 1/3. An improper fraction, on the other hand, has a numerator (the top number) that is larger than or equal to its denominator (the bottom number). To simplify a mixed number, we first convert it into an improper fraction, a format more amenable to simplification.
1 1/3 is a mixed number. The whole number is 1, and the fraction is 1/3. To convert this to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 x 3 = 3
- Add the numerator to the result: 3 + 1 = 4
- Keep the same denominator: 3
Therefore, 1 1/3 is equivalent to the improper fraction 4/3.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Once we find the GCD, we divide both the numerator and denominator by it.
Let's find the GCD of 4 and 3. The factors of 4 are 1, 2, and 4. The factors of 3 are 1 and 3. The only common factor is 1. Therefore, the GCD of 4 and 3 is 1.
Simplifying 4/3: The Final Step
Since the GCD of 4 and 3 is 1, dividing both the numerator and denominator by 1 doesn't change the value of the fraction. This means that 4/3 is already in its simplest form. There's no further simplification possible.
Therefore, 1 1/3 in its simplest form is 4/3. While it might seem counterintuitive that an improper fraction is considered "simplest," remember that simplification aims for the lowest terms, not necessarily a mixed number.
A Deeper Dive into Fraction Simplification: Prime Factorization
While finding the GCD by listing factors works well for smaller numbers, prime factorization is a more systematic approach for larger numbers. Prime factorization involves expressing a number as the product of its prime factors (numbers divisible only by 1 and themselves).
Let's illustrate this with an example. Suppose we need to simplify the fraction 12/18.
- Find the prime factorization of the numerator (12): 12 = 2 x 2 x 3 = 2² x 3
- Find the prime factorization of the denominator (18): 18 = 2 x 3 x 3 = 2 x 3²
- Identify common prime factors: Both 12 and 18 share one factor of 2 and one factor of 3.
- Find the GCD: The GCD is the product of the common prime factors raised to their lowest power. In this case, the GCD is 2 x 3 = 6.
- Simplify the fraction: Divide both the numerator and denominator by the GCD (6): 12/6 = 2 and 18/6 = 3.
- Simplified fraction: The simplified fraction is 2/3.
Applications of Fraction Simplification
Simplifying fractions isn't just an academic exercise; it has practical applications in various areas:
- Everyday Calculations: When dealing with recipes, measurements, or sharing items, simplifying fractions makes calculations easier and more intuitive.
- Engineering and Construction: Precise measurements and calculations are crucial in these fields, and simplifying fractions ensures accuracy.
- Computer Science: Fractions are used in algorithms and data structures, and simplification improves efficiency and readability.
- Financial Calculations: Working with percentages, interest rates, and proportions often involves fractions, and simplification improves clarity and accuracy in financial calculations.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to understand and work with. Simplified fractions are more concise and less prone to errors in calculations. They also provide a clearer representation of the relationship between the numerator and the denominator.
Q2: Can I simplify a fraction by dividing only the numerator or only the denominator?
A2: No. To simplify a fraction, you must divide both the numerator and the denominator by the same number (their GCD). Dividing only one part changes the value of the fraction.
Q3: What if the GCD of the numerator and denominator is 1?
A3: If the GCD is 1, the fraction is already in its simplest form. It cannot be simplified further.
Q4: How do I simplify fractions with larger numbers?
A4: For larger numbers, prime factorization is a more efficient method to find the GCD. Alternatively, you can use the Euclidean algorithm, a more advanced technique for finding the GCD.
Q5: Are there any online tools or calculators to simplify fractions?
A5: Yes, numerous online calculators and tools can simplify fractions. However, understanding the underlying process is crucial for mastering fraction simplification.
Conclusion
Simplifying fractions, including mixed numbers like 1 1/3, is a fundamental skill in mathematics with far-reaching applications. By understanding the concept of the greatest common divisor (GCD) and employing techniques like prime factorization, we can efficiently reduce fractions to their lowest terms. Remember that the simplest form of 1 1/3 is 4/3, highlighting the importance of working with improper fractions for accurate simplification. Mastering fraction simplification not only enhances mathematical proficiency but also provides a solid foundation for more advanced mathematical concepts. Practice is key; the more you work with fractions, the more comfortable and efficient you'll become.
Latest Posts
Latest Posts
-
Gcf Of 45 And 30
Sep 18, 2025
-
29 2 As A Decimal
Sep 18, 2025
-
5662 Sq Ft To Acres
Sep 18, 2025
-
Gcf Of 42 And 12
Sep 18, 2025
-
2 To The 11th Power
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 1/3 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.