1 1 4 Simplest Form
saludintensiva
Sep 16, 2025 · 6 min read
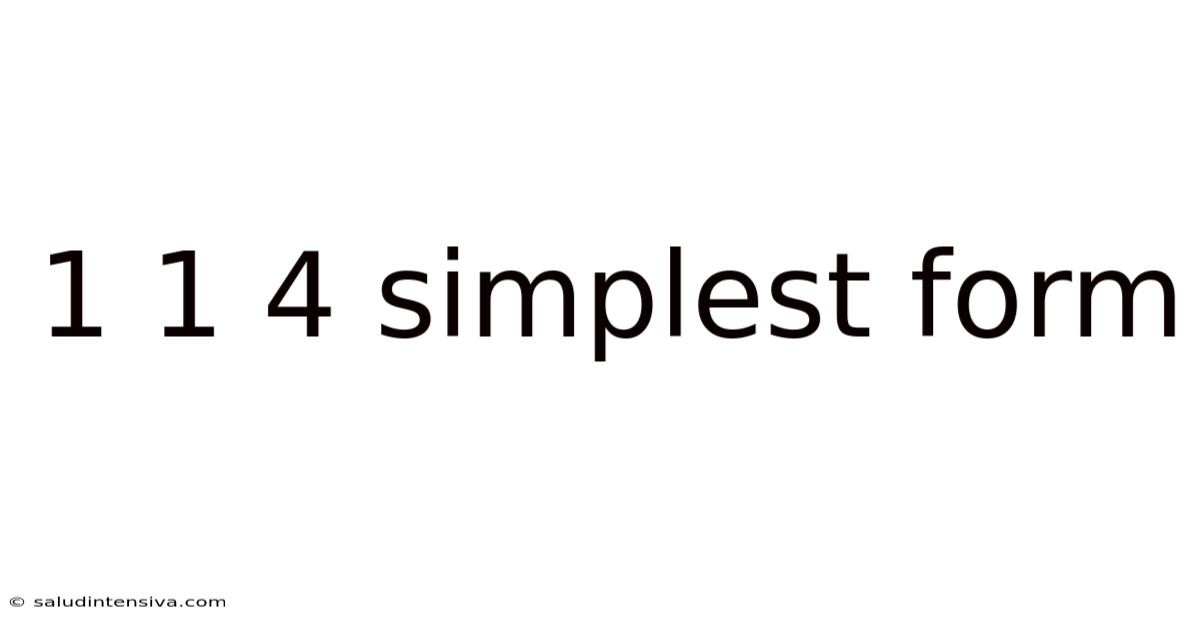
Table of Contents
Simplifying Fractions: Understanding 1/1 and 4 in its Simplest Form
Have you ever encountered a fraction and wondered, "Is this fraction in its simplest form?" Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide will delve into the concept of simplifying fractions, focusing specifically on the examples of 1/1 and 4, and provide a solid foundation for tackling more complex fraction simplification problems. We'll explore the underlying principles, step-by-step procedures, and even address frequently asked questions. By the end, you'll not only know how to simplify 1/1 and 4 but also possess the confidence to simplify any fraction.
Understanding Fractions: A Quick Recap
Before we dive into simplifying 1/1 and 4, let's briefly refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 and the denominator is 4. This means we have 3 out of 4 equal parts.
Simplifying Fractions: The Core Concept
Simplifying a fraction means reducing it to its lowest terms. This involves finding the greatest common divisor (GCD), also known as the highest common factor (HCF), of the numerator and the denominator and dividing both by that number. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. The simplified fraction will have the same value as the original fraction but will be expressed more concisely.
Simplifying 1/1: A Special Case
The fraction 1/1 represents one whole unit divided into one equal part. This is already in its simplest form. There is no common divisor (other than 1) between the numerator (1) and the denominator (1). Therefore, simplifying 1/1 results in 1/1 or simply 1. Any number divided by itself equals 1.
Expressing 4 as a Fraction and Simplifying
The number 4 can be expressed as a fraction by placing it over 1: 4/1. This represents four whole units. To simplify this fraction, we look for the GCD of the numerator (4) and the denominator (1). The GCD of 4 and 1 is 1. Dividing both the numerator and the denominator by 1 does not change the value of the fraction. Therefore, the simplest form of 4/1 remains 4/1, or simply 4.
Step-by-Step Guide to Simplifying Fractions
Let's outline a general step-by-step process for simplifying any fraction:
-
Find the GCD (Greatest Common Divisor): Determine the greatest common divisor of the numerator and the denominator. You can do this by listing the factors of each number and identifying the largest factor they share. Alternatively, you can use the Euclidean algorithm, a more efficient method for larger numbers.
-
Divide Both Numerator and Denominator: Divide both the numerator and the denominator by their GCD.
-
Check for Further Simplification: Examine the resulting fraction to ensure it cannot be simplified further. If the GCD of the new numerator and denominator is still greater than 1, repeat steps 1 and 2.
Example: Simplify the fraction 12/18
-
Find the GCD: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The GCD of 12 and 18 is 6.
-
Divide: 12 ÷ 6 = 2 and 18 ÷ 6 = 3.
-
Simplified Fraction: The simplified fraction is 2/3.
Understanding Prime Factorization and its Role in Simplification
Prime factorization is a powerful tool for finding the GCD. Prime factorization involves expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Example: Let's find the GCD of 24 and 36 using prime factorization:
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2² (or 4) and the lowest power of 3 is 3¹. Therefore, the GCD is 2² x 3 = 4 x 3 = 12.
Dividing both 24 and 36 by 12 gives us the simplified fraction 2/3.
Real-World Applications of Fraction Simplification
Simplifying fractions is not just an academic exercise; it has numerous practical applications in various fields:
-
Cooking and Baking: Following recipes often requires understanding and simplifying fractions to accurately measure ingredients.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on working with fractions and simplifying them for accuracy.
-
Finance: Calculating interest, discounts, and proportions in finance often involves fraction simplification.
-
Data Analysis: Simplifying fractions can aid in interpreting and presenting data in a clear and concise manner.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
A1: Simplifying fractions makes them easier to understand, compare, and use in calculations. A simplified fraction represents the same value as the original fraction but in a more concise form.
Q2: What if I get a fraction where the numerator is larger than the denominator?
A2: This is an improper fraction. You can simplify it in the same way as a proper fraction (where the numerator is smaller than the denominator), and then convert it to a mixed number (a whole number and a proper fraction) if needed.
Q3: Are there any online tools to simplify fractions?
A3: Yes, many online calculators and websites can simplify fractions automatically. However, understanding the underlying process is crucial for developing your mathematical skills.
Q4: What happens if the GCD is 1?
A4: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form.
Q5: How can I improve my skills in simplifying fractions?
A5: Practice regularly! Work through various examples, try using different methods for finding the GCD, and challenge yourself with more complex fractions.
Conclusion
Simplifying fractions is a fundamental skill with broad applications across various fields. Understanding the concept of the greatest common divisor and using prime factorization are key tools in this process. While fractions like 1/1 are already in their simplest form and 4, expressed as 4/1, remains 4/1 in its simplest form, the principles discussed here are applicable to any fraction, no matter how complex. Mastering fraction simplification will strengthen your mathematical foundation and enhance your problem-solving abilities in numerous contexts. Regular practice and a clear understanding of the underlying principles will ensure confidence and proficiency in tackling fraction simplification tasks. Remember, the journey to mastering mathematics is one of consistent effort and focused learning. Keep practicing, and you'll be surprised at how quickly you improve!
Latest Posts
Latest Posts
-
39 40 As A Decimal
Sep 16, 2025
-
3 To The 1 2 Power
Sep 16, 2025
-
17 24 As A Percentage
Sep 16, 2025
-
What Is 4 Of 85000
Sep 16, 2025
-
How To Calculate Percentage Excel
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.