1 1 4 X 3
saludintensiva
Sep 17, 2025 · 6 min read
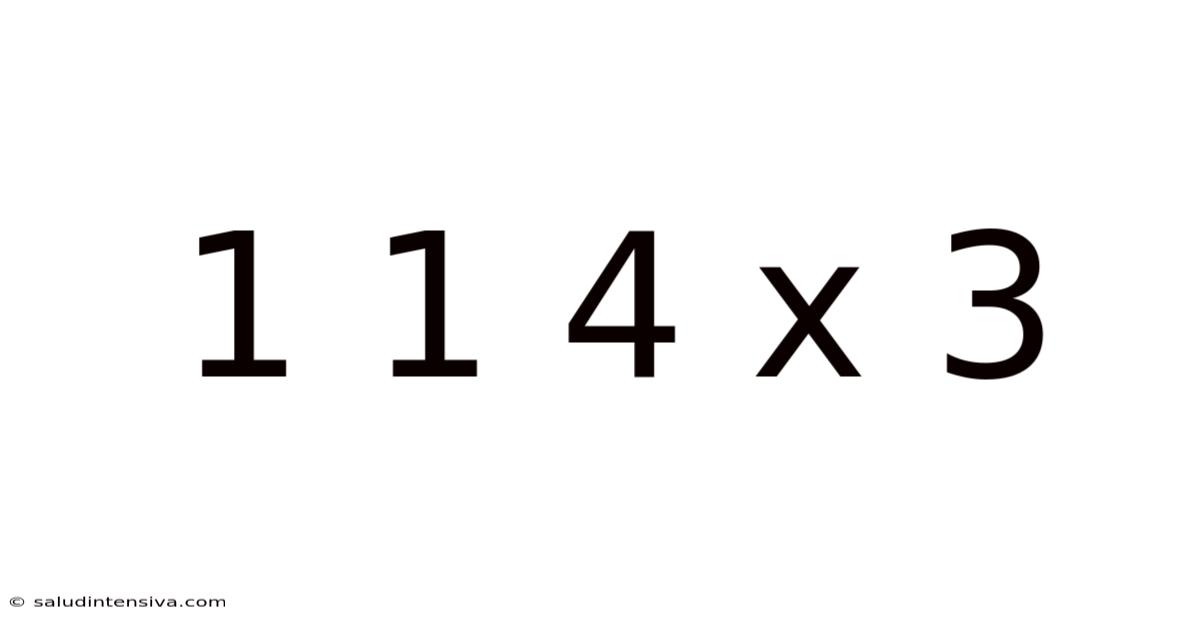
Table of Contents
Decoding 1 1 4 x 3: Exploring the Multifaceted Implications of a Seemingly Simple Expression
This article delves into the seemingly simple mathematical expression "1 1 4 x 3," exploring its various interpretations, applications, and the underlying principles involved. While seemingly straightforward, this expression offers a rich opportunity to explore different mathematical concepts, problem-solving strategies, and the importance of clarity and precision in mathematical notation. We will unravel the ambiguity, address potential interpretations, and ultimately arrive at a comprehensive understanding. This exploration will be beneficial for students of mathematics, as well as anyone interested in enhancing their problem-solving skills and appreciating the nuances of mathematical language.
Understanding the Ambiguity: The Importance of Notation
The primary challenge with interpreting "1 1 4 x 3" lies in its ambiguous notation. The absence of explicit operators between the numbers creates multiple possibilities. This highlights the critical importance of precise mathematical notation. A single misplaced symbol or the omission of an operator can lead to vastly different results. Let's examine the potential interpretations.
Interpretation 1: Concatenation and Multiplication
One plausible interpretation treats "1 1 4" as a concatenated number (114) and then performs multiplication. In this case, the expression becomes:
114 x 3 = 342
This approach assumes that the spaces are merely separators and not indicative of any mathematical operation. While seemingly simple, this interpretation underscores the importance of clear notation to avoid confusion.
Interpretation 2: Multiple Additions and Multiplication
Another interpretation involves treating the spaces as plus signs, converting the expression to:
1 + 1 + 4 x 3
Following the order of operations (PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), we first perform the multiplication:
4 x 3 = 12
Then, we add the remaining numbers:
1 + 1 + 12 = 14
This approach reveals the critical role of the order of operations in determining the correct result. Ignoring the order of operations would lead to an incorrect answer.
Interpretation 3: A Sequence with an Unknown Operation
A more abstract interpretation might consider "1 1 4" as a sequence or pattern. However, without additional context or information, it’s impossible to determine a definitive operation or rule governing this sequence. This interpretation emphasizes the necessity of complete information when dealing with mathematical problems. We need a clearly defined relationship between the numbers to establish a pattern.
Exploring Deeper Mathematical Concepts
Beyond the immediate calculations, the expression "1 1 4 x 3" can serve as a springboard for exploring more profound mathematical concepts.
Order of Operations: The Foundation of Mathematical Computation
The ambiguity of the original expression highlights the crucial role of the order of operations (PEMDAS/BODMAS). Understanding and correctly applying this fundamental principle is essential for accurate mathematical computations. The order dictates the sequence in which operations are performed, ensuring consistent and unambiguous results. Without the order of operations, mathematical expressions would be chaotic and unpredictable.
Number Systems and Representation: From Digits to Meaning
The expression implicitly touches upon number systems and their representation. The decimal system, which we implicitly use here, relies on place value. Understanding place value is fundamental to interpreting numbers and performing arithmetic operations. Each digit in a number holds a specific weight based on its position. For example, in the number 114, the '1' in the hundreds place represents 100, while the '1' in the tens place represents 10, and the '4' in the units place represents 4.
Algebraic Thinking: Generalizing the Expression
While the expression itself is numerical, we can introduce algebraic thinking by generalizing it. For instance, we could represent the expression as:
a b c x d
Where 'a', 'b', 'c', and 'd' are variables. This allows us to explore different combinations of numbers and analyze the resulting outcomes. This approach lays the groundwork for more advanced mathematical concepts like functions and equations.
Pattern Recognition and Sequence Analysis
Although we couldn't definitively determine a pattern in the "1 1 4" sequence without further information, this type of problem-solving encourages the development of pattern recognition skills. This skill is crucial in various fields, from mathematics and science to computer programming and data analysis.
Practical Applications and Real-World Relevance
While seemingly abstract, the principles illustrated by interpreting "1 1 4 x 3" have practical applications in various fields.
Programming and Coding: The Importance of Syntax
In programming, the equivalent of ambiguous notation is flawed syntax. Similar to our mathematical expression, incorrect syntax leads to errors and prevents the program from functioning correctly. Programmers must adhere to strict syntax rules to ensure their code is executed as intended.
Data Analysis and Interpretation: Avoiding Ambiguity in Data Representation
In data analysis, clear and unambiguous data representation is crucial for accurate interpretation. Ambiguity can lead to misinterpretations and flawed conclusions. Data analysts must pay close attention to data formatting and notation to ensure the integrity of their analysis.
Engineering and Design: Precision in Calculations
In engineering and design, precision in calculations is paramount. Ambiguous calculations can have serious consequences. Engineers rely on mathematical principles and precise notation to ensure the safety and functionality of their designs.
Everyday Calculations: From Shopping to Budgeting
Even in everyday life, clear understanding of mathematical principles, including order of operations, is necessary for accurate calculations. Whether it’s calculating the total cost of groceries or managing a budget, precise mathematical skills are essential.
Frequently Asked Questions (FAQ)
Q1: What is the correct answer to "1 1 4 x 3"?
A1: There's no single "correct" answer without clarifying the intended operations. Depending on the interpretation, the answer could be 342 (concatenation and multiplication) or 14 (addition and multiplication). The ambiguity highlights the need for precise mathematical notation.
Q2: Why is clear mathematical notation so important?
A2: Clear notation prevents ambiguity and ensures consistent interpretation of mathematical expressions. It eliminates the potential for errors and allows for effective communication of mathematical ideas.
Q3: What if there were parentheses in the expression?
A3: Parentheses would significantly alter the interpretation. For example, (1 + 1 + 4) x 3 would unequivocally yield 18. Parentheses dictate the order of operations, removing ambiguity.
Q4: How can I improve my skills in interpreting mathematical expressions?
A4: Practice is key. Work through various mathematical problems, paying close attention to notation and the order of operations. Seek clarification when encountering ambiguous expressions. Focus on understanding the underlying principles rather than just memorizing formulas.
Conclusion: The Value of Precision and Critical Thinking
The seemingly simple expression "1 1 4 x 3" offers a valuable lesson in the importance of precise mathematical notation and the critical thinking required to interpret ambiguous information. It underscores the fundamental role of the order of operations, the significance of number representation, and the potential for exploring deeper mathematical concepts from a seemingly straightforward problem. This exploration highlights the need for clarity and precision in all mathematical endeavors, from simple calculations to complex scientific analyses. The ability to critically analyze and interpret ambiguous information is a vital skill that extends far beyond the realm of mathematics, impacting problem-solving in numerous areas of life. By understanding the nuances of mathematical language and applying sound problem-solving strategies, we can approach even the most seemingly simple problems with a deeper understanding and a higher chance of arriving at the correct solution.
Latest Posts
Latest Posts
-
What Is 4 Of 14000
Sep 17, 2025
-
200 Sq Ft Room Dimensions
Sep 17, 2025
-
5 8 Is Equal To
Sep 17, 2025
-
Is 7 16 Bigger Than 3 8
Sep 17, 2025
-
3 4 Divided By 3
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 1 4 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.