1/10 000 As A Decimal
saludintensiva
Sep 16, 2025 · 5 min read
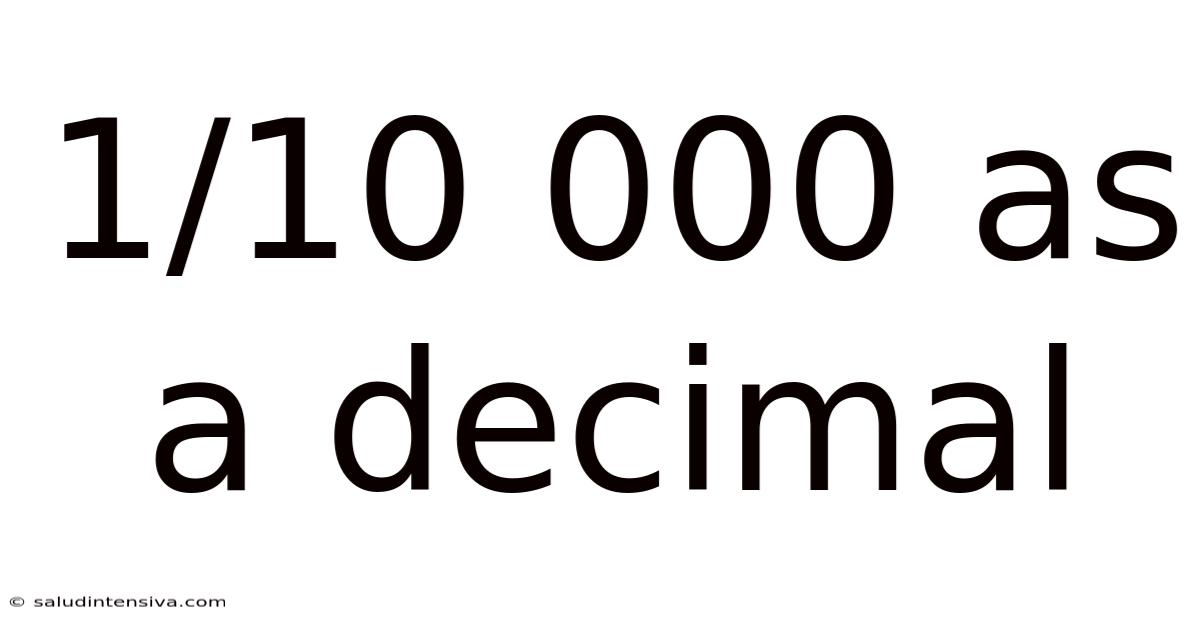
Table of Contents
Understanding 1/10,000 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article delves into the conversion of the fraction 1/10,000 into its decimal form, exploring the underlying principles, providing step-by-step instructions, and addressing frequently asked questions. We'll also examine the broader context of decimal representation and its significance in various fields.
Introduction: From Fractions to Decimals
Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). A decimal, on the other hand, uses a base-ten system to represent a number, utilizing a decimal point to separate the whole number part from the fractional part. Converting a fraction to a decimal involves dividing the numerator by the denominator. This seemingly simple process unlocks a deeper understanding of numerical representation and its practical applications. This article specifically focuses on converting the fraction 1/10,000 to its decimal equivalent, offering a clear and detailed explanation suitable for learners of all levels.
Method 1: Direct Division
The most straightforward approach to converting 1/10,000 to a decimal is through direct division. We simply divide the numerator (1) by the denominator (10,000):
1 ÷ 10,000 = 0.0001
This process highlights the core principle: the denominator dictates the place value of the decimal. Since we're dividing by 10,000 (which is 10<sup>4</sup>), the result will have four decimal places.
Method 2: Understanding Place Value
To further solidify the understanding, let's explore the concept of place value. The decimal system is based on powers of 10. Each place to the right of the decimal point represents a decreasing power of 10:
- 10<sup>-1</sup> = 0.1 (tenths)
- 10<sup>-2</sup> = 0.01 (hundredths)
- 10<sup>-3</sup> = 0.001 (thousandths)
- 10<sup>-4</sup> = 0.0001 (ten-thousandths)
Since 1/10,000 represents one ten-thousandth, it directly corresponds to the 10<sup>-4</sup> place value, resulting in the decimal 0.0001.
Method 3: Scientific Notation
Scientific notation provides a concise way to represent very small or very large numbers. It expresses a number as a product of a coefficient (a number between 1 and 10) and a power of 10. For 1/10,000, the scientific notation is:
1 x 10<sup>-4</sup>
This representation clearly shows the magnitude of the number and its relationship to powers of 10. To convert this back to decimal form, we simply move the decimal point four places to the left, giving us 0.0001.
The Significance of Decimal Representation
The decimal representation of 1/10,000, or 0.0001, is more than just a numerical conversion; it has broad implications across numerous fields:
-
Engineering and Technology: In engineering design and calculations, precision is paramount. Decimal representation facilitates accurate measurements and calculations, particularly in areas such as microelectronics, where dimensions are often measured in micrometers or nanometers. 0.0001 represents a significant difference in such contexts.
-
Finance: In financial transactions, decimals are crucial for representing percentages, interest rates, and currency values. Accurate decimal representation ensures correct calculations of interest payments, profits, and losses. Small discrepancies, even at the ten-thousandth place, can have significant cumulative effects over time.
-
Science: Scientific measurements often involve extremely small or large numbers. Decimal representation, often coupled with scientific notation, makes it easier to handle and analyze these numbers. In fields like chemistry and physics, dealing with quantities at the atomic level requires high precision in decimal representation.
-
Data Analysis: Data analysis heavily relies on precise numerical representation. Decimals are essential for statistical calculations, creating accurate charts, graphs, and visualizations. The accuracy of data analysis heavily depends on the precision of the decimal representations used.
-
Computer Science: Computers use binary systems (base-2), but they readily translate these into decimal representations for human readability. Understanding decimal equivalents is critical in programming, especially when dealing with floating-point numbers and precision issues.
Practical Applications and Real-World Examples
Let's illustrate the practical relevance of 1/10,000 (0.0001) with some examples:
-
Measurement: If you're measuring the thickness of a material in millimeters and get a reading of 0.0001 millimeters, it shows a very thin layer.
-
Percentages: 0.0001 represents 0.01% (0.0001 * 100%). This small percentage could still be meaningful in certain contexts. For example, a 0.01% change in a large population could still represent a considerable number of individuals.
-
Finance: A 0.0001 change in the price of a stock might seem insignificant, but when multiplied by a high volume of shares, it can represent a substantial financial impact.
-
Manufacturing: In precision manufacturing, a tolerance of 0.0001 units (e.g., millimeters or inches) is often required to ensure that parts fit together correctly and function as intended. Failing to meet such tolerances could lead to malfunctioning equipment.
Frequently Asked Questions (FAQ)
-
Q: Can 1/10,000 be expressed as a percentage?
-
A: Yes. To convert a decimal to a percentage, multiply by 100. 0.0001 x 100 = 0.01%.
-
Q: What is the reciprocal of 1/10,000?
-
A: The reciprocal of a fraction is obtained by swapping the numerator and denominator. The reciprocal of 1/10,000 is 10,000/1, or simply 10,000.
-
Q: How do I convert other fractions to decimals?
-
A: The general method is to divide the numerator by the denominator. For more complex fractions, you might need to use long division or a calculator.
-
Q: Are there limitations to decimal representation?
-
A: Yes, there are limitations. Some fractions, like 1/3, result in repeating decimals (0.333...). Computers have limitations in representing all decimal numbers with perfect accuracy due to their finite memory.
Conclusion: Mastering Decimal Representation
Understanding the conversion of fractions like 1/10,000 to their decimal equivalents is crucial for developing a strong foundation in mathematics. The process itself is straightforward, but its implications extend far beyond simple calculations. From engineering and finance to science and computer science, the ability to accurately represent and manipulate decimal numbers is an essential skill for success in numerous fields. This article provides a thorough understanding of the conversion process and highlights the practical relevance of decimal representation in various real-world scenarios. By mastering these concepts, you'll not only improve your mathematical skills but also gain valuable insights into the fundamental building blocks of quantitative reasoning.
Latest Posts
Latest Posts
-
What Is Half Of 31
Sep 16, 2025
-
5 1 4 As A Percent
Sep 16, 2025
-
1330 Military Time To Normal
Sep 16, 2025
-
Convert Mm To Sq Ft
Sep 16, 2025
-
Lcm Of 25 30 35
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1/10 000 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.