1 14 As A Percent
saludintensiva
Sep 15, 2025 · 6 min read
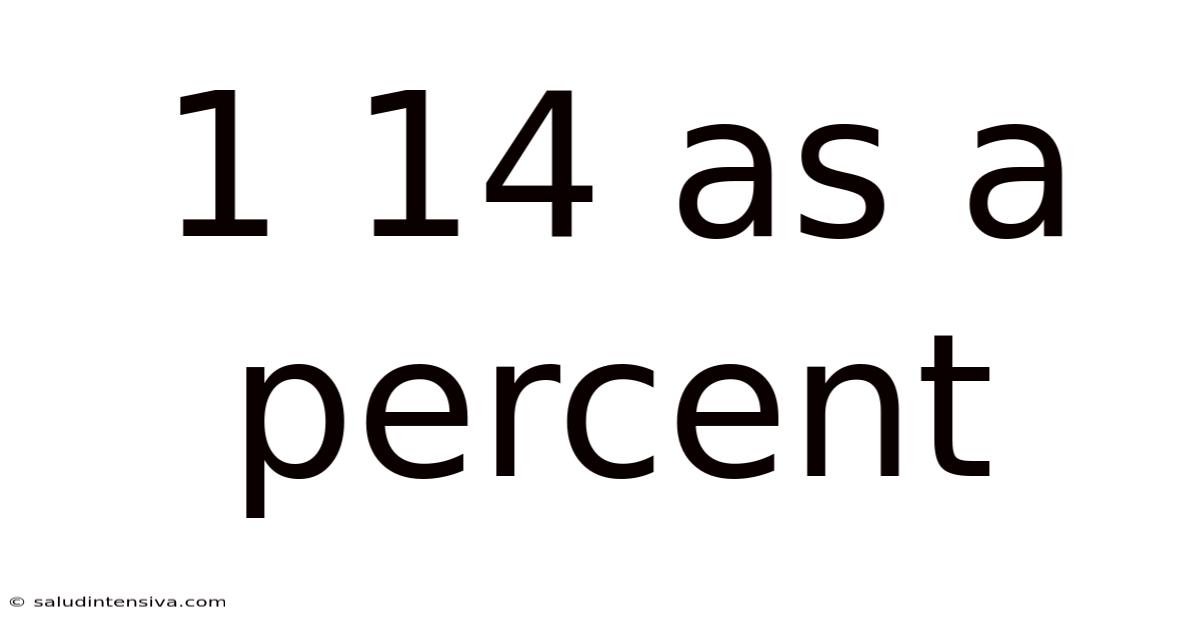
Table of Contents
Understanding 1/14 as a Percentage: A Comprehensive Guide
Fractions and percentages are fundamental concepts in mathematics with widespread applications in everyday life, from calculating discounts and tips to understanding financial reports and scientific data. Converting fractions to percentages is a crucial skill, and this article will provide a thorough explanation of how to convert the fraction 1/14 into a percentage, along with exploring related concepts and practical applications. This guide will equip you with the knowledge to confidently handle similar fraction-to-percentage conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion of 1/14, let's briefly review the definitions of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/14, 1 is the numerator and 14 is the denominator. This means we have 1 part out of a total of 14 equal parts.
A percentage is a way of expressing a number as a fraction of 100. It uses the symbol "%" to represent "out of 100" or "per hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or simplified, 1/2.
Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100, and then expressing the numerator as a percentage.
Converting 1/14 to a Percentage: Step-by-Step
There are two primary methods to convert 1/14 into a percentage:
Method 1: Direct Division
This method involves dividing the numerator (1) by the denominator (14) and then multiplying the result by 100 to express it as a percentage.
-
Divide the numerator by the denominator: 1 ÷ 14 ≈ 0.07142857
-
Multiply the result by 100: 0.07142857 × 100 ≈ 7.142857%
Therefore, 1/14 is approximately equal to 7.14%. We often round percentages to a certain number of decimal places for practical purposes. Rounding to two decimal places, we get 7.14%.
Method 2: Equivalent Fraction Method
This method involves finding an equivalent fraction with a denominator of 100. While this is not always straightforward and often leads to a non-terminating decimal, it provides a conceptual understanding of the process.
To make the denominator 100, we would need to multiply 14 by a number that results in 100. Unfortunately, 100 is not divisible by 14 without leaving a remainder. This means we cannot directly find an equivalent fraction with a denominator of 100. This illustrates why the direct division method is generally preferred for fractions that don't easily convert to a denominator of 100. However, let's explore the concept.
If we were dealing with a fraction that could easily be converted, the process would look like this: For example, converting 1/2 to a percentage:
-
Find a multiplier to make the denominator 100: 100 / 2 = 50
-
Multiply both numerator and denominator by the multiplier: (1 × 50) / (2 × 50) = 50/100
-
Express as a percentage: 50/100 = 50%
As you can see, 1/2 is equivalent to 50%. This method works best with fractions that have denominators that are factors of 100 (e.g., 2, 4, 5, 10, 20, 25, 50). Since 14 is not a factor of 100, the direct division method provides a more efficient solution.
Understanding the Result: 7.14%
The result of 7.14% (rounded) means that 1/14 represents approximately 7.14 parts out of every 100 parts. This percentage can be used in various contexts:
- Discounts: A 7.14% discount on an item would reduce its price by 7.14% of its original cost.
- Tax Rates: A tax rate of 7.14% would mean that for every $100, $7.14 would be paid as tax.
- Survey Results: If 1 out of 14 people surveyed preferred a particular option, the percentage of people preferring that option would be 7.14%.
- Financial Analysis: In financial statements, percentages are often used to represent ratios and proportions. Understanding the percentage equivalent of a fraction is crucial for interpreting these reports.
Practical Applications and Examples
Let's consider some real-world examples illustrating the application of converting 1/14 to a percentage:
Example 1: A Class Test
If 1 out of 14 students in a class scored 100% on a test, the percentage of students scoring 100% would be approximately 7.14%.
Example 2: Sales Figures
If a company sold 1 item out of every 14 items produced, their sales success rate would be approximately 7.14%.
Example 3: Inventory Management
If 1 out of 14 components in a shipment is defective, the percentage of defective components is approximately 7.14%.
Expanding on the Concept: Working with More Complex Fractions
The principles demonstrated for converting 1/14 can be applied to other fractions. The key steps remain the same: divide the numerator by the denominator and multiply by 100. Even with more complex fractions, this process holds true. For example, converting 3/7 to a percentage:
-
Divide: 3 ÷ 7 ≈ 0.42857
-
Multiply by 100: 0.42857 × 100 ≈ 42.86%
Frequently Asked Questions (FAQ)
Q1: Why do we multiply by 100 when converting a fraction to a percentage?
A1: We multiply by 100 because a percentage is a fraction out of 100. Multiplying by 100 scales the decimal result to represent the fraction as a proportion of 100.
Q2: What if the resulting percentage has many decimal places?
A2: In many real-world applications, it is sufficient to round the percentage to a reasonable number of decimal places (e.g., two decimal places). The level of precision required depends on the context of the problem.
Q3: Are there any online calculators that can perform this conversion?
A3: Yes, many online calculators are available that can convert fractions to percentages quickly and accurately. However, understanding the underlying mathematical process is crucial for applying this knowledge in various situations.
Q4: Can I convert a percentage back to a fraction?
A4: Yes! To convert a percentage back to a fraction, simply divide the percentage by 100 and simplify the resulting fraction. For example, 7.14% would be 7.14/100, which can be simplified (although it would be an approximate simplification due to the decimal in 7.14).
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill applicable across numerous disciplines. This article provided a detailed explanation of how to convert 1/14 to a percentage (approximately 7.14%), utilizing both the direct division and equivalent fraction methods. Understanding these methods empowers you to confidently tackle similar conversions and apply this knowledge to solve problems in various contexts, from simple daily calculations to complex financial analyses. Remember to practice regularly to strengthen your understanding and speed. By mastering this skill, you'll gain a more comprehensive grasp of numerical relationships and improve your ability to analyze and interpret quantitative data.
Latest Posts
Latest Posts
-
Multiples Of 4 And 7
Sep 15, 2025
-
Thwyl Mn Bawnd Ala Kylw
Sep 15, 2025
-
How Long Is 4 Meters
Sep 15, 2025
-
81 F To Degree Celsius
Sep 15, 2025
-
Gcf Of 7 And 21
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 14 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.