1 15 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
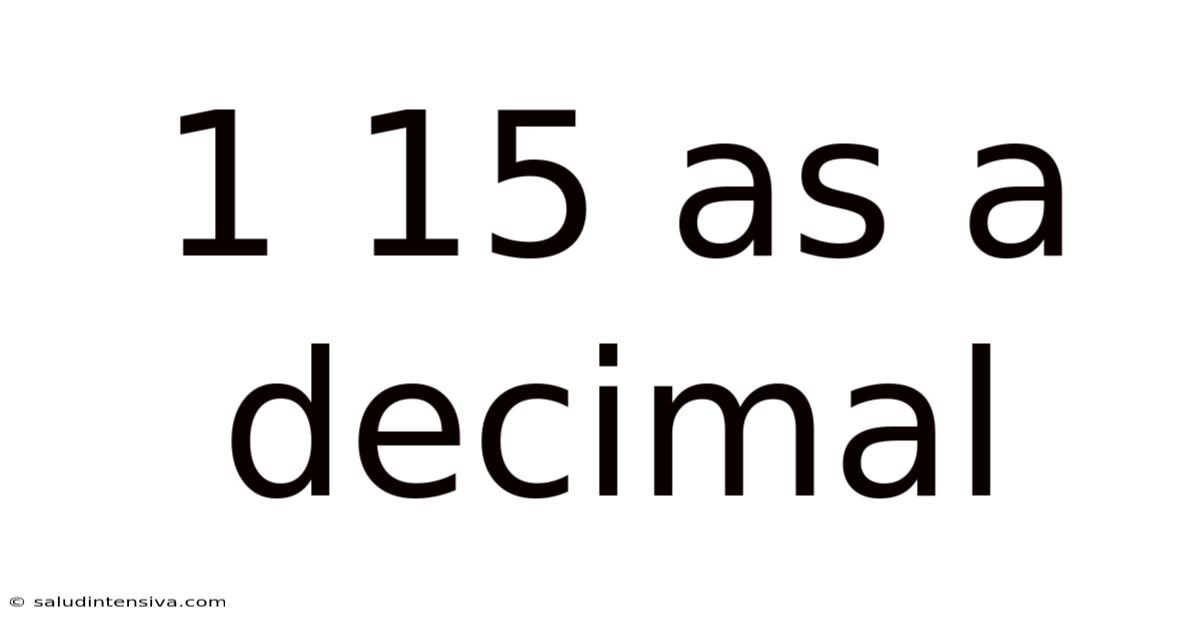
Table of Contents
1/15 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the conversion of the fraction 1/15 to its decimal equivalent, exploring different methods and providing a detailed explanation of the underlying principles. We'll also examine the significance of this conversion and its implications in different contexts. By the end, you'll not only know the decimal value of 1/15 but also possess a robust understanding of fraction-to-decimal conversion techniques.
Understanding Fractions and Decimals
Before we jump into converting 1/15, let's briefly revisit the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/15, 1 is the numerator and 15 is the denominator. This means we are considering one part out of fifteen equal parts of a whole.
A decimal, on the other hand, represents a number in base-10, using a decimal point to separate the whole number part from the fractional part. Decimals are another way of representing fractions, particularly those with denominators that are powers of 10 (10, 100, 1000, etc.).
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. We divide the numerator (1) by the denominator (15):
1 ÷ 15 = ?
Since 1 is smaller than 15, we add a decimal point and a zero to the dividend (1 becomes 1.0). Now we perform the long division:
0.0666...
15 | 1.0000
-0
---
10
-0
--
100
-90
---
100
-90
---
10
As you can see, the division results in a repeating decimal: 0.0666... The digit 6 repeats infinitely. This is often represented as 0.0̅6.
Therefore, 1/15 as a decimal is 0.0666... or 0.0̅6.
Method 2: Converting to an Equivalent Fraction with a Denominator that is a Power of 10
While long division provides a direct method, another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10. This method, however, is not always feasible, especially for fractions with denominators that don't have factors of 2 or 5 (prime factors of 10).
In this case, finding a power of 10 that is divisible by 15 is not straightforward. 15 (3 x 5) doesn't readily lead to a power of 10. Therefore, this method is less efficient for 1/15 compared to long division.
Method 3: Using a Calculator
A simple and efficient way to convert 1/15 to a decimal is to use a calculator. Simply enter 1 ÷ 15 and the calculator will display the decimal equivalent: 0.066666...
Understanding Repeating Decimals
The result of converting 1/15 to a decimal is a repeating decimal, also known as a recurring decimal. This means the decimal representation contains a sequence of digits that repeat infinitely. In this case, the digit 6 repeats indefinitely. Repeating decimals are common when converting fractions to decimals, especially those with denominators that are not factors of powers of 10.
Understanding repeating decimals is crucial in various mathematical applications, particularly in calculations involving infinite series and limits.
Significance and Applications of the Decimal Equivalent of 1/15
The decimal equivalent of 1/15, 0.0̅6, might seem like a simple result, but its implications extend beyond basic arithmetic. Understanding this conversion becomes important in various fields:
-
Financial Calculations: When dealing with percentages or proportions in finance, converting fractions to decimals simplifies calculations. For example, if you need to calculate 1/15 of a total amount, converting it to 0.0̅6 makes the calculation easier.
-
Scientific Computations: In scientific fields, precision is paramount. Converting fractions to decimals helps in calculations where decimal representation is preferred, enabling easier manipulation and analysis of data.
-
Engineering and Design: In engineering and design, accurate calculations are essential. Converting fractions to decimals ensures that measurements and calculations are precise and consistent.
-
Computer Programming: Many programming languages require decimal representation for numerical calculations. Understanding fraction-to-decimal conversion is crucial for developing accurate and efficient programs.
-
Everyday Life: Though seemingly less obvious, converting fractions to decimals is crucial for everyday tasks such as calculating tips, dividing portions, or understanding discounts.
Frequently Asked Questions (FAQ)
Q: Why does 1/15 result in a repeating decimal?
A: A fraction results in a repeating decimal when its denominator contains prime factors other than 2 and 5 (the prime factors of 10). Since 15 has a prime factor of 3, it leads to a repeating decimal.
Q: How can I round 0.0̅6 to a specific number of decimal places?
A: You can round 0.0̅6 to any desired number of decimal places. For example:
- Rounded to two decimal places: 0.07
- Rounded to three decimal places: 0.067
- Rounded to four decimal places: 0.0667
The rounding rules dictate whether to round up or down based on the digit following the desired decimal place.
Q: Are there any other fractions that result in repeating decimals?
A: Yes, many fractions result in repeating decimals. Any fraction whose denominator has prime factors other than 2 and 5 will produce a repeating decimal. Examples include 1/3 (0.3̅3), 1/7 (0.1̅42857), and 1/11 (0.0̅9).
Q: What is the difference between a terminating decimal and a repeating decimal?
A: A terminating decimal is a decimal that ends after a finite number of digits. A repeating decimal continues infinitely with a repeating sequence of digits.
Conclusion
Converting 1/15 to its decimal equivalent, 0.0̅6, involves a straightforward process using long division. This seemingly simple conversion has significant implications in various applications, highlighting the importance of understanding fraction-to-decimal conversion in mathematics and beyond. Mastering this skill empowers you to handle various calculations with greater accuracy and efficiency, enhancing your problem-solving abilities in numerous contexts. Remember, understanding the underlying principles, such as the role of prime factors in determining terminating versus repeating decimals, deepens your comprehension of the mathematical concepts involved.
Latest Posts
Latest Posts
-
Gcf For 18 And 45
Sep 10, 2025
-
6 13 As A Percentage
Sep 10, 2025
-
What Is 10 In Decimal
Sep 10, 2025
-
Factors Of 16 In Pairs
Sep 10, 2025
-
Lcm Of 10 And 25
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 15 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.