1 2 2 1 3
saludintensiva
Sep 18, 2025 · 6 min read
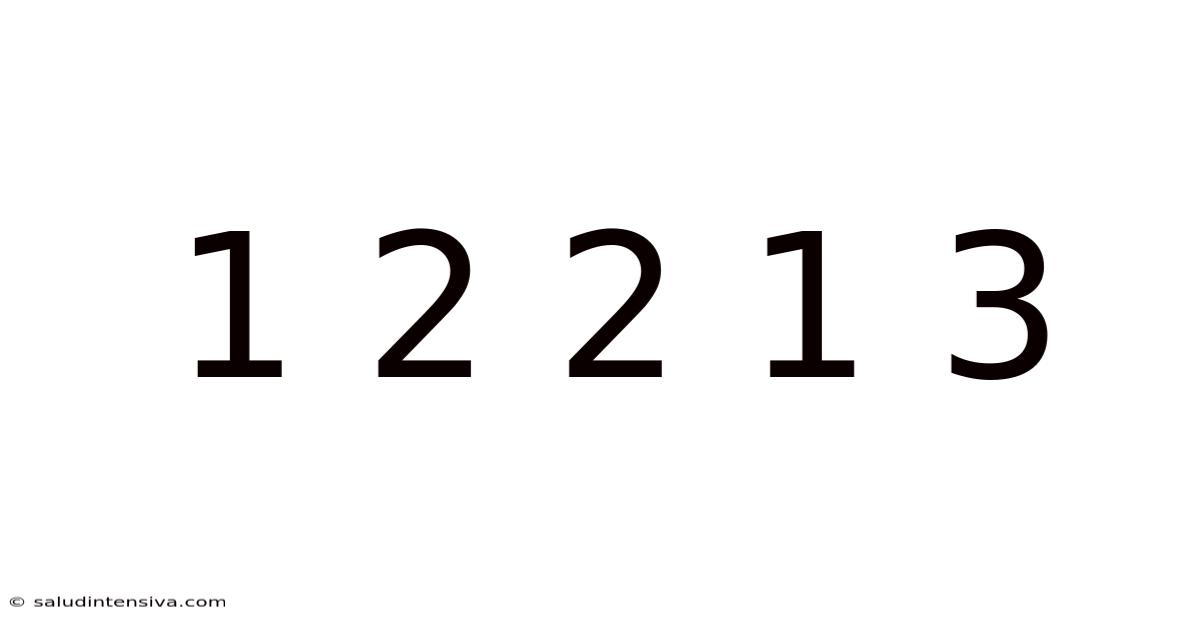
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Artistic Potential of 1 2 2 1 3
The seemingly simple sequence "1 2 2 1 3" might appear innocuous at first glance. However, this numerical arrangement holds surprising potential for exploration across various fields, from mathematical analysis and pattern recognition to artistic expression and creative problem-solving. This article will delve deep into the multifaceted nature of this sequence, examining its potential interpretations, underlying patterns, and the possibilities it unlocks for further investigation. We will explore its mathematical properties, analyze potential underlying structures, and consider its potential applications in creative endeavors. This exploration will highlight the often-unseen connections between seemingly disparate fields, showcasing the boundless capacity for discovery inherent in even the simplest of sequences.
Understanding the Sequence: Initial Observations
The sequence 1 2 2 1 3 presents itself as a seemingly arbitrary string of numbers. Yet, the very act of observing it prompts questions: Is it random? Does it follow a specific rule or pattern? Does it relate to any known mathematical concepts? These are precisely the questions that drive our exploration. The lack of immediate, obvious patterns only increases its intrigue. The absence of a readily apparent rule encourages us to consider various possibilities and develop strategies to uncover potential hidden structures.
Mathematical Analysis: Exploring Potential Patterns
The immediate challenge lies in identifying a governing rule. Several potential approaches exist:
-
Difference Analysis: Examining the differences between consecutive numbers (2-1=1, 2-2=0, 1-2=-1, 3-1=2) yields a new sequence (1, 0, -1, 2). This doesn't reveal an obvious pattern, but it opens avenues for further investigation using higher-order differences.
-
Ratio Analysis: Similarly, examining the ratios between consecutive numbers doesn't immediately suggest a consistent pattern.
-
Modular Arithmetic: Exploring the sequence within a modular arithmetic system (e.g., modulo 3, modulo 4, etc.) could reveal cyclical patterns or relationships not immediately evident in the standard decimal system.
-
Fibonacci-like Sequences: While not directly a Fibonacci sequence (where each number is the sum of the two preceding ones), the sequence might exhibit similarities to other types of recursive sequences. We can investigate if modifying the recursive rule slightly could generate a sequence resembling 1 2 2 1 3.
Searching for Underlying Structures: Beyond Simple Rules
Given the lack of an immediately apparent rule, we might consider more complex underlying structures. This approach moves beyond the search for simple arithmetic relationships to encompass:
-
Transformations: Could this sequence be the result of a transformation applied to another, more recognizable sequence? Imagine a sequence undergoing operations like shifting, mirroring, or adding a constant. We need to identify potential parent sequences and the transformations that could produce 1 2 2 1 3.
-
Geometric Interpretations: Can the sequence be visualized geometrically? We could represent each number as a dimension or a step in a geometrical pattern. Exploring these visual representations might reveal previously hidden connections.
-
Combinatorial Analysis: Does the sequence relate to combinatorial structures or arrangements? Consider possibilities such as permutations, combinations, or partitions of a small set of numbers. This could unveil a deeper mathematical significance.
-
Symbolic Interpretation: Moving beyond purely numerical interpretation, we might view the sequence as a symbolic representation. Each number could represent a different concept, action, or element in a system. This symbolic lens might unveil narratives or patterns concealed within the sequence’s structure.
Expanding the Possibilities: Iterative Processes and Recursion
An often fruitful approach in pattern recognition involves extending the sequence and observing emerging patterns. However, extending the sequence requires a defined rule. We might attempt to generate further numbers by hypothesising rules and iteratively refining them based on the results. This approach necessitates a creative and iterative process, combining intuition with mathematical rigor. Here are a few examples of possible iterative processes:
-
Rule 1: Alternating additions and subtractions: One could posit a rule where odd-positioned numbers are added to the next number and even-positioned numbers are subtracted from the next number. The result would not reproduce the sequence perfectly, but would generate a new sequence related to the original.
-
Rule 2: Modular arithmetic transformations: We might create a rule based on modular arithmetic, performing modulo operations to generate subsequent numbers.
-
Rule 3: Recursive rules based on combinations of previous terms: Similar to the Fibonacci sequence, one could devise recursive rules that generate new terms based on combinations of previous terms in the sequence.
Artistic and Creative Applications: The Sequence as Inspiration
Beyond mathematical analysis, the sequence 1 2 2 1 3 offers significant potential for creative expression. Consider these possibilities:
-
Musical Composition: The sequence could serve as a basis for musical composition, dictating the rhythm, duration of notes, or the structure of a musical phrase.
-
Visual Art: The sequence could inspire the creation of visual art, determining the size, number, or arrangement of elements in a painting, sculpture, or digital artwork.
-
Literary Expression: The sequence might inspire a narrative structure, the number of chapters in a book, or the rhythmic patterns of a poem. Each number could represent a different stage or character in the story.
-
Choreography: The sequence could be used to structure a dance piece, determining the number of steps, movements, or dancers involved in each section.
-
Game Design: The sequence could inspire the rules or progression in a game, affecting the structure of game levels or the rewards system.
Further Exploration and Open Questions
The sequence 1 2 2 1 3 presents a fertile ground for continued exploration. Many questions remain open:
-
Is there a deeper mathematical structure underlying this sequence? This question necessitates further investigation into diverse mathematical areas.
-
Can the sequence be generalized? Are there similar sequences that share underlying patterns or structures?
-
What are the limits of its creative application? Exploring diverse creative fields using this sequence as a foundation could reveal novel and unexpected forms of expression.
-
Can we develop algorithms that generate sequences with similar properties? The creation of algorithms to generate similar sequences would further our understanding of the mathematical principles underlying such patterns.
-
Does this sequence appear naturally in other contexts? Could it represent a fundamental structure found in nature, physics, or other scientific fields?
Conclusion: The Enduring Mystery and Potential of a Simple Sequence
The initial simplicity of the sequence 1 2 2 1 3 belies its inherent complexity and potential. Our exploration has demonstrated the richness of mathematical and artistic avenues unlocked by this seemingly innocuous numerical arrangement. The lack of a readily apparent rule fuels further investigation, inviting diverse approaches and encouraging a creative blend of mathematical analysis and artistic interpretation. The sequence serves as a microcosm of the endless possibilities inherent in seemingly simple systems, highlighting the beauty and power of pattern recognition, creative exploration, and the enduring mystery that underpins the mathematical and artistic worlds. Its exploration underscores the importance of persistent questioning, iterative experimentation, and the boundless potential for discovery that awaits those willing to delve deeper into the seemingly ordinary. The journey of understanding this sequence is not merely about finding a single "correct" answer but about the process of exploration, the development of creative problem-solving skills, and the appreciation of the unexpected connections between seemingly disparate fields.
Latest Posts
Latest Posts
-
How To Find A Dimension
Sep 18, 2025
-
Is 1 2 Greater Than 1 6
Sep 18, 2025
-
How Much Is 50 Kg
Sep 18, 2025
-
14 Weeks Back From Today
Sep 18, 2025
-
What Is 1 2 2 6
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 2 2 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.