1 2 Minus 1 3
saludintensiva
Sep 11, 2025 · 6 min read
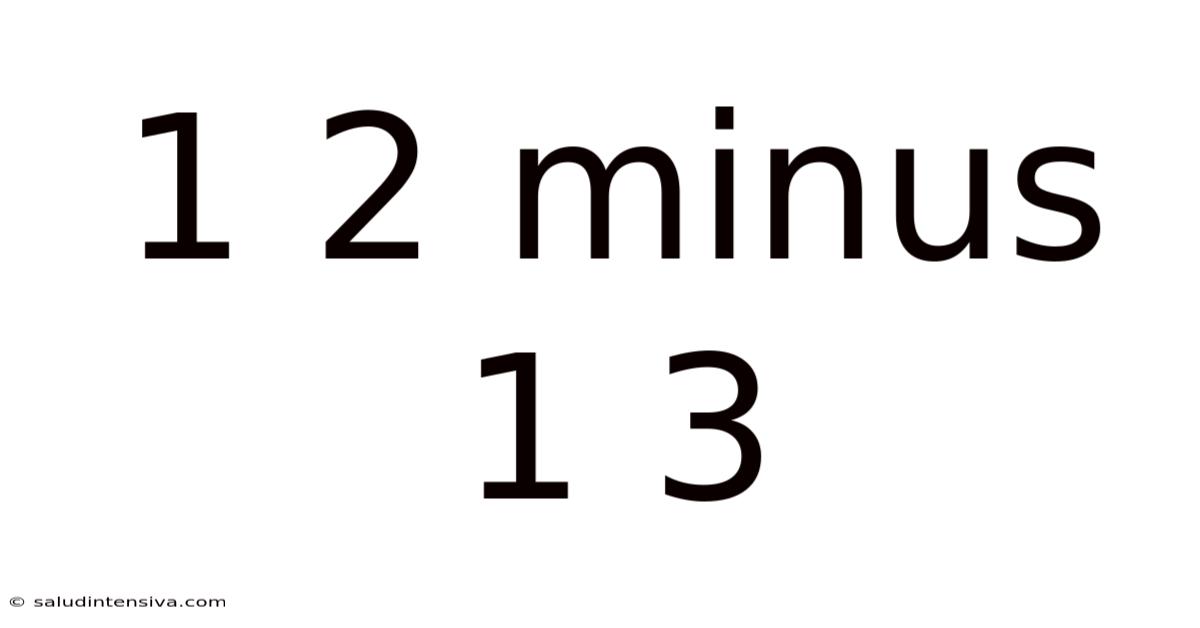
Table of Contents
Decoding 1/2 Minus 1/3: A Deep Dive into Fraction Subtraction
Understanding fraction subtraction can seem daunting at first, but with a structured approach, it becomes surprisingly straightforward. This article delves into the seemingly simple problem of 1/2 minus 1/3 (1/2 - 1/3), explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common misconceptions. We'll equip you with the tools to tackle similar fraction subtraction problems with confidence.
Introduction: Why Fractions Matter
Fractions are fundamental to mathematics and appear in countless real-world applications, from cooking and construction to finance and computer science. Mastering fraction operations, including subtraction, is crucial for building a solid mathematical foundation. This article specifically addresses the subtraction of unlike fractions, meaning fractions with different denominators, a common stumbling block for many learners. We'll break down the process of subtracting 1/2 - 1/3, demonstrating a method applicable to a wide range of fraction subtraction problems.
Step-by-Step Solution: Subtracting 1/2 Minus 1/3
The core challenge in subtracting 1/2 - 1/3 lies in the fact that these are unlike fractions. Unlike fractions have different denominators (the bottom number in a fraction). To subtract them, we need to find a common denominator.
Step 1: Finding the Least Common Denominator (LCD)
The LCD is the smallest number that is a multiple of both denominators. For 2 and 3, the multiples are:
- Multiples of 2: 2, 4, 6, 8, 10...
- Multiples of 3: 3, 6, 9, 12...
The smallest number appearing in both lists is 6. Therefore, the LCD of 2 and 3 is 6.
Step 2: Converting to Equivalent Fractions
Now, we convert both fractions to equivalent fractions with the LCD (6) as the denominator. To do this, we multiply the numerator and denominator of each fraction by the appropriate factor:
- For 1/2: We multiply both the numerator and denominator by 3 (because 2 x 3 = 6): (1 x 3) / (2 x 3) = 3/6
- For 1/3: We multiply both the numerator and denominator by 2 (because 3 x 2 = 6): (1 x 2) / (3 x 2) = 2/6
Step 3: Performing the Subtraction
Now that we have equivalent fractions with the same denominator, we can subtract the numerators:
3/6 - 2/6 = (3 - 2) / 6 = 1/6
Therefore, 1/2 - 1/3 = 1/6
Visual Representation: Understanding Fractions Geometrically
A visual approach can greatly aid comprehension. Imagine a rectangle divided into six equal parts. One-half (1/2) represents three of these parts (3/6), while one-third (1/3) represents two of these parts (2/6). Subtracting 1/3 from 1/2 visually means removing two parts from the three, leaving one part out of six, hence 1/6.
Explanation of the Mathematical Principles
The process of finding a common denominator and converting fractions is based on the fundamental principle of equivalent fractions. An equivalent fraction represents the same value as the original fraction but has a different numerator and denominator. This is achieved by multiplying (or dividing) both the numerator and denominator by the same non-zero number. This doesn't change the value of the fraction because it's essentially multiplying by 1 (e.g., 3/3 = 1).
The reason we need a common denominator before subtracting is that we can only directly subtract (or add) the numerators when the denominators are the same. Think of it like adding apples and oranges – you can't directly add them unless you convert them to a common unit, like "fruit." Similarly, fractions with different denominators represent different units of measurement, and we need to convert them to a common unit (the common denominator) before we can perform the operation.
Dealing with More Complex Fraction Subtraction
The method outlined above can be generalized to subtract any two (or more) unlike fractions:
-
Find the LCD: Determine the least common denominator of all the fractions involved. This often involves finding the prime factorization of the denominators and identifying the highest power of each prime factor.
-
Convert to Equivalent Fractions: Convert each fraction to an equivalent fraction with the LCD as the denominator.
-
Perform the Subtraction: Subtract the numerators, keeping the common denominator.
-
Simplify (if necessary): Reduce the resulting fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor (GCD).
Example: Subtract 2/5 - 1/4
-
LCD: The LCD of 5 and 4 is 20.
-
Equivalent Fractions:
- 2/5 = (2 x 4) / (5 x 4) = 8/20
- 1/4 = (1 x 5) / (4 x 5) = 5/20
-
Subtraction: 8/20 - 5/20 = 3/20
-
Simplification: 3/20 is already in its simplest form.
Frequently Asked Questions (FAQ)
Q1: What if the fractions are mixed numbers (e.g., 1 1/2 - 2/3)?
A1: First, convert the mixed numbers to improper fractions. For example, 1 1/2 becomes (1 x 2 + 1) / 2 = 3/2. Then, follow the steps for subtracting unlike fractions.
Q2: What if the result of the subtraction is an improper fraction?
A2: Convert the improper fraction back to a mixed number. For example, if you get 7/4, divide 7 by 4: 7 ÷ 4 = 1 with a remainder of 3. So, 7/4 = 1 3/4.
Q3: How do I find the LCD of more than two fractions?
A3: Find the prime factorization of each denominator. The LCD will be the product of the highest powers of all the prime factors present in the denominators. For example, for the fractions 1/6, 1/15, and 1/10:
- 6 = 2 x 3
- 15 = 3 x 5
- 10 = 2 x 5
The LCD is 2 x 3 x 5 = 30.
Q4: Can I use a calculator to solve fraction subtraction problems?
A4: While calculators can perform fraction subtraction, understanding the underlying principles is crucial for building mathematical proficiency and solving more complex problems. Calculators should be used as a tool to check your work, not to replace the learning process.
Conclusion: Mastering Fraction Subtraction
Subtracting fractions, even unlike fractions, is a manageable task with a systematic approach. By understanding the concept of equivalent fractions, finding the least common denominator, and following the step-by-step process, you can confidently solve a wide range of fraction subtraction problems. Remember, practice is key. The more you work with fractions, the more comfortable and proficient you'll become. This foundational skill will serve you well in numerous mathematical and real-world applications. Don't be discouraged by initial challenges; with consistent effort, you'll master this essential mathematical skill.
Latest Posts
Latest Posts
-
2 3 7 As A Decimal
Sep 11, 2025
-
5 100 As A Decimal
Sep 11, 2025
-
What Time Is 14 37
Sep 11, 2025
-
Equivalent Fraction For 3 10
Sep 11, 2025
-
Round To The Nearest Year
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Minus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.