1 2 Minus 1 4
saludintensiva
Sep 17, 2025 · 6 min read
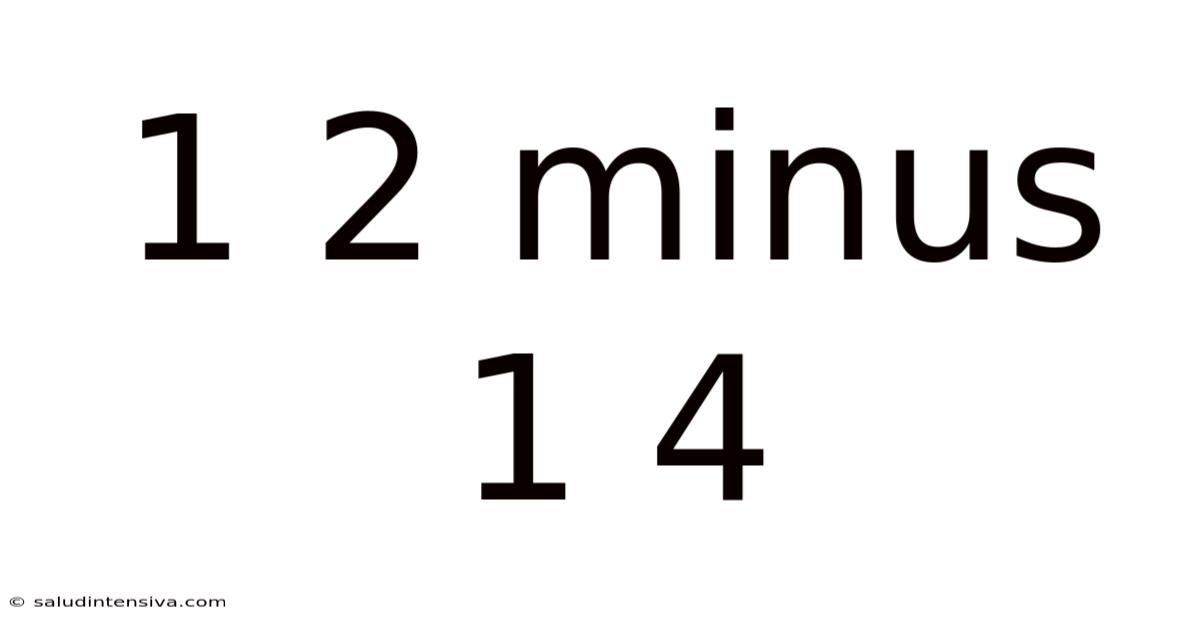
Table of Contents
Decoding 1/2 Minus 1/4: A Deep Dive into Fraction Subtraction
This article provides a comprehensive guide to understanding and solving the seemingly simple subtraction problem: 1/2 - 1/4. We'll move beyond the basic answer to explore the underlying mathematical principles, various methods of solving similar problems, and practical applications. This explanation is designed for learners of all levels, from those just grasping fractions to those looking to solidify their understanding of arithmetic operations.
Introduction: Understanding Fractions
Before tackling the subtraction, let's establish a firm understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts, and the numerator (1) indicates we're considering one of those parts. Similarly, 1/4 represents one out of four equal parts.
Understanding fractions is crucial for various aspects of life, from cooking and sewing to advanced mathematics and engineering. This seemingly basic concept forms the foundation for numerous complex calculations.
Solving 1/2 - 1/4: The Method of Common Denominators
The key to subtracting (or adding) fractions is to ensure they share a common denominator. This means both fractions must have the same denominator. In our problem, 1/2 and 1/4 have different denominators. To proceed, we need to find a common denominator.
The easiest way to find a common denominator is often to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. In this case, the denominators are 2 and 4. The multiples of 2 are 2, 4, 6, 8... and the multiples of 4 are 4, 8, 12... The smallest number that appears in both lists is 4. Therefore, 4 is the least common denominator (LCD).
Now, we need to rewrite both fractions with the common denominator of 4:
- 1/2: To change the denominator from 2 to 4, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4
The fraction 1/2 is now equivalent to 2/4. Remember, multiplying both the numerator and denominator by the same number doesn't change the value of the fraction – it only changes its representation.
Now our subtraction problem becomes: 2/4 - 1/4
Subtracting fractions with a common denominator is straightforward: subtract the numerators and keep the denominator the same.
2/4 - 1/4 = (2 - 1) / 4 = 1/4
Therefore, 1/2 - 1/4 = 1/4
Visual Representation: Understanding Fractions Geometrically
Visual aids can significantly improve understanding. Let's visualize this subtraction using a simple diagram.
Imagine a circle representing a whole.
- 1/2: Divide the circle in half. Shading one half represents 1/2.
- 1/4: Now, divide the same circle into four equal quarters. Shading one quarter represents 1/4.
- Subtraction: Compare the shaded areas. You'll see that the difference between shading one half and shading one quarter leaves one quarter shaded. This visually confirms our answer: 1/2 - 1/4 = 1/4
Alternative Methods: Decimal Conversion
Another approach is to convert the fractions into decimals before performing the subtraction.
- 1/2: 1/2 = 0.5
- 1/4: 1/4 = 0.25
Now, subtract the decimals:
0.5 - 0.25 = 0.25
Since 0.25 is equivalent to 1/4, we arrive at the same answer. This method can be helpful when dealing with more complex fractions or when using a calculator.
Expanding the Concept: More Complex Fraction Subtraction
Let's extend our understanding by tackling a slightly more challenging problem: 3/5 - 1/10
- Find the LCD: The LCM of 5 and 10 is 10.
- Rewrite the fractions:
- 3/5 = (3 x 2) / (5 x 2) = 6/10
- Subtract: 6/10 - 1/10 = (6 - 1) / 10 = 5/10
- Simplify: 5/10 can be simplified by dividing both numerator and denominator by 5, resulting in 1/2.
Therefore, 3/5 - 1/10 = 1/2
Dealing with Mixed Numbers: A Comprehensive Example
Mixed numbers combine a whole number and a fraction (e.g., 2 1/3). Let's consider the subtraction of mixed numbers: 2 1/2 - 1 1/4
- Convert to improper fractions: An improper fraction has a numerator larger than or equal to its denominator.
- 2 1/2 = (2 x 2 + 1) / 2 = 5/2
- 1 1/4 = (1 x 4 + 1) / 4 = 5/4
- Find the LCD: The LCD of 2 and 4 is 4.
- Rewrite the fractions: 5/2 = (5 x 2) / (2 x 2) = 10/4
- Subtract: 10/4 - 5/4 = (10 - 5) / 4 = 5/4
- Convert back to a mixed number (optional): 5/4 = 1 1/4
Therefore, 2 1/2 - 1 1/4 = 1 1/4
Practical Applications of Fraction Subtraction
Fraction subtraction isn't just a classroom exercise; it has widespread practical applications:
- Cooking & Baking: Adjusting recipes, calculating ingredient quantities, and measuring portions often involve fraction subtraction.
- Construction & Engineering: Precise measurements are crucial, and calculations involving fractions are commonplace.
- Finance: Managing budgets, calculating discounts, and understanding interest rates all utilize fractional arithmetic.
- Data Analysis: Working with datasets and percentages frequently requires manipulating fractions.
Frequently Asked Questions (FAQ)
Q: What if the denominators don't have a common factor?
A: If the denominators are relatively prime (they share no common factors other than 1), you simply multiply the denominators to find the common denominator. For example, to subtract 1/3 - 1/5, the common denominator would be 15 (3 x 5).
Q: Can I use a calculator for fraction subtraction?
A: Yes, many calculators have built-in fraction functions that simplify the process. However, understanding the underlying principles is crucial for problem-solving beyond simple calculations.
Q: What happens if the numerator in the subtraction is smaller than the other numerator?
A: You'll get a negative fraction. For instance, 1/4 - 3/4 = -2/4 = -1/2
Q: How do I simplify fractions after subtraction?
A: Simplify by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that number. For example, 6/12 simplifies to 1/2 because the GCD of 6 and 12 is 6.
Conclusion: Mastering Fraction Subtraction
Mastering fraction subtraction involves understanding the concept of common denominators, the ability to convert between fractions and decimals, and the application of these principles to solve various types of problems, including those involving mixed numbers. By practicing regularly and utilizing visual aids when needed, you can confidently tackle any fraction subtraction problem and appreciate its practical significance in numerous real-world scenarios. Remember, consistent practice and a clear understanding of the underlying concepts are key to building a strong foundation in mathematics. Don't be afraid to break down complex problems into smaller, more manageable steps. The journey to mathematical fluency is rewarding, and each step you take brings you closer to achieving mastery.
Latest Posts
Latest Posts
-
Gcf Of 36 And 30
Sep 17, 2025
-
Meters Per Second To Rpm
Sep 17, 2025
-
Gcf Of 18 And 50
Sep 17, 2025
-
First 10 Multiples Of 7
Sep 17, 2025
-
How Long Is 280 Minutes
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Minus 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.