1 3 Plus 1 6
saludintensiva
Sep 15, 2025 · 6 min read
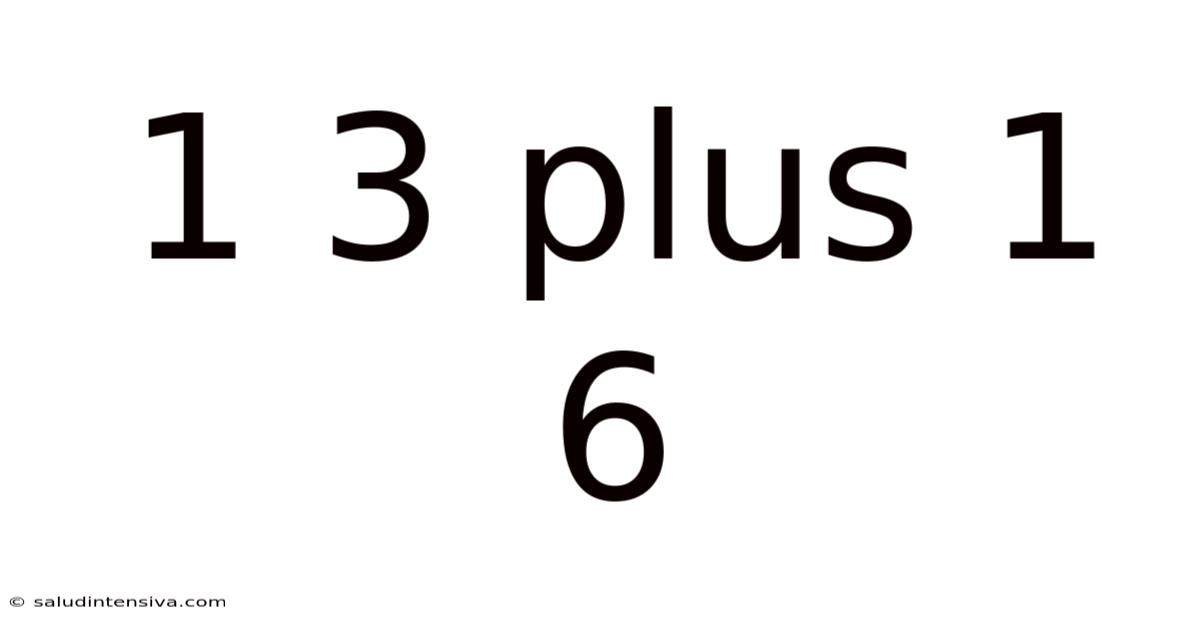
Table of Contents
Decoding 1 + 3 + 1 + 6: A Journey into Number Theory, Logic, and Problem Solving
This article delves into the seemingly simple mathematical expression "1 + 3 + 1 + 6," exploring its various interpretations and expanding on the underlying principles of number theory, logic, and problem-solving. While the immediate answer is straightforward (11), we'll unpack the richness hidden within this expression, revealing its potential for deeper learning and application in various fields. This exploration will be beneficial for students, educators, and anyone interested in the beauty and power of mathematics.
The Obvious Answer and its Limitations
The most basic interpretation of "1 + 3 + 1 + 6" is a straightforward addition problem. Adding the numbers together yields a sum of 11. This is the immediate and readily apparent answer. However, this simplistic approach overlooks the potential for deeper analysis and exploration of the numbers' inherent properties and the context in which the expression is presented. We'll move beyond this elementary calculation to explore more complex and fascinating possibilities.
Number Theory Perspectives: Exploring the Numbers
Let's delve into the individual numbers: 1, 3, 1, and 6. Each holds unique properties within the realm of number theory.
-
1 (One): The multiplicative identity; it's the foundation of arithmetic, as multiplying any number by 1 leaves it unchanged. It's also the first natural number and a fundamental unit in various mathematical systems.
-
3 (Three): An odd prime number, meaning it's only divisible by 1 and itself. It's the second smallest prime number and plays a significant role in many mathematical concepts.
-
6 (Six): A composite number (not prime), it's the product of 2 and 3 (2 x 3 = 6). It's also a perfect number, meaning the sum of its proper divisors (1, 2, and 3) equals the number itself (1 + 2 + 3 = 6). This characteristic makes it a unique and interesting number in number theory.
The repetition of the number 1 adds an interesting layer. Its recurrence might hint at a pattern or signify a specific mathematical context we haven't yet considered. This repetition demands a deeper investigation into potential patterns or underlying structures.
Logic and Pattern Recognition: Beyond Simple Addition
Moving beyond simple addition, we can explore potential patterns or sequences that might explain the given numbers. Could this be a fragment of a larger sequence? Let's investigate some possibilities:
-
Arithmetic Progression: Is there a common difference between consecutive numbers? In this case, no consistent arithmetic progression is apparent.
-
Geometric Progression: Is there a common ratio between consecutive numbers? Again, no consistent geometric progression is evident.
-
Fibonacci Sequence: The Fibonacci sequence (0, 1, 1, 2, 3, 5, 8, 13…) is famous for its appearance in nature and mathematics. Our numbers don't directly fit this sequence.
-
Other Number Sequences: Many other number sequences exist (e.g., Lucas numbers, Catalan numbers). Further exploration might reveal a connection to one of these sequences, but it's not immediately obvious.
The lack of an immediately apparent pattern suggests that the expression "1 + 3 + 1 + 6" might not represent a mathematical sequence in a conventional sense. This doesn't diminish its significance; it simply suggests that we need to explore further possibilities and broaden our perspective.
Exploring Potential Contextual Interpretations
The meaning of "1 + 3 + 1 + 6" could depend heavily on the context in which it's presented. Let's imagine some possible scenarios:
-
Coding/Programming: In computer programming, these numbers could represent variables, memory addresses, or elements in an array. Their sum might be irrelevant; the individual values and their order are crucial.
-
Discrete Mathematics/Combinatorics: The numbers could represent sets, permutations, or combinations within a combinatorial problem. The sum is less important than the relationships between the numbers and the structures they form.
-
Game Theory/Decision Making: Each number could represent a choice or outcome in a game. The sum becomes less relevant than the strategy involved in selecting and utilizing these numbers.
-
Base Systems: The numbers could be interpreted in different number bases (e.g., binary, ternary, hexadecimal). In a different base, the sum might vary. However, without explicit specification of the base, we assume the standard base 10.
These examples highlight how the meaning of the expression can extend beyond the simple arithmetic operation. The numbers themselves are less important than the context and how they're used within the specific problem.
Problem-Solving Strategies: Applying Mathematical Thinking
The exploration of "1 + 3 + 1 + 6" isn't just about finding the sum; it's about developing problem-solving skills. Here are some key strategies to consider when approaching similar mathematical challenges:
-
Identify the Information: What do we know? We have four numbers: 1, 3, 1, and 6.
-
Define the Objective: What do we need to find? The most basic objective is the sum. However, we've expanded this to explore deeper meanings.
-
Consider Different Approaches: We explored various methods, including simple addition, searching for patterns, and examining possible contexts.
-
Use Appropriate Tools: This problem didn't require sophisticated tools, but more complex mathematical problems might require specialized software or techniques.
-
Evaluate the Result: The initial sum is 11. However, our exploration revealed a much richer understanding of the underlying mathematical principles and the importance of context.
-
Iterative Process: Problem-solving is often an iterative process. We may need to adjust our approach and test different hypotheses until we find a satisfying solution.
Through this exercise, we've illustrated a practical application of a powerful mathematical concept: breaking down a problem into smaller, more manageable parts, exploring various approaches, and using critical thinking skills.
Frequently Asked Questions (FAQ)
Q: Is there a hidden pattern in the numbers 1, 3, 1, and 6?
A: While no immediately obvious arithmetic or geometric pattern exists, exploring different number sequences might reveal a connection. However, it is equally plausible that the arrangement is arbitrary. The lack of an obvious pattern doesn't diminish the importance of exploring other potential interpretations.
Q: Could the numbers represent something other than their numerical value?
A: Absolutely. As demonstrated earlier, the numbers could represent variables, memory locations, elements in a set, or choices in a game depending on the context. Their meaning is heavily context-dependent.
Q: What is the significance of the repeated '1'?
A: The repeated '1' could be purely coincidental, or it could be a significant part of a more complex pattern that requires more data points to decipher. Without further context, we can't definitively say.
Q: Is this expression useful in real-world applications?
A: The expression itself might seem trivial. However, the problem-solving strategies employed in its analysis are highly valuable and transferable to numerous real-world scenarios, especially those involving data analysis, pattern recognition, and logical deduction.
Q: Can the expression be solved using different mathematical operations?
A: While the basic interpretation involves addition, the context might permit other mathematical operations. Without specified context, addition remains the most logical choice.
Conclusion: Beyond the Sum of 11
While the immediate answer to "1 + 3 + 1 + 6" is 11, the journey of exploring this simple expression has unveiled a wealth of insights into number theory, logic, and problem-solving methodologies. The exploration highlights the importance of considering context, recognizing that the same numbers can hold different meanings depending on the situation. The value lies not only in arriving at the numerical answer but also in developing critical thinking skills, exploring alternative interpretations, and embracing a multifaceted approach to problem-solving. This seemingly trivial mathematical expression serves as a powerful reminder of the richness and depth hidden within the seemingly simple world of numbers. The exercise encourages a flexible and inquisitive mindset, crucial for tackling more complex and nuanced challenges in mathematics and beyond.
Latest Posts
Latest Posts
-
What Is 3 4kg In Pounds
Sep 15, 2025
-
Square Root Of 1 2
Sep 15, 2025
-
Is 9 Prime Or Composite
Sep 15, 2025
-
15 20 As A Percent
Sep 15, 2025
-
All The Factors Of 24
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Plus 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.