1 3 X 1 6
saludintensiva
Sep 19, 2025 · 5 min read
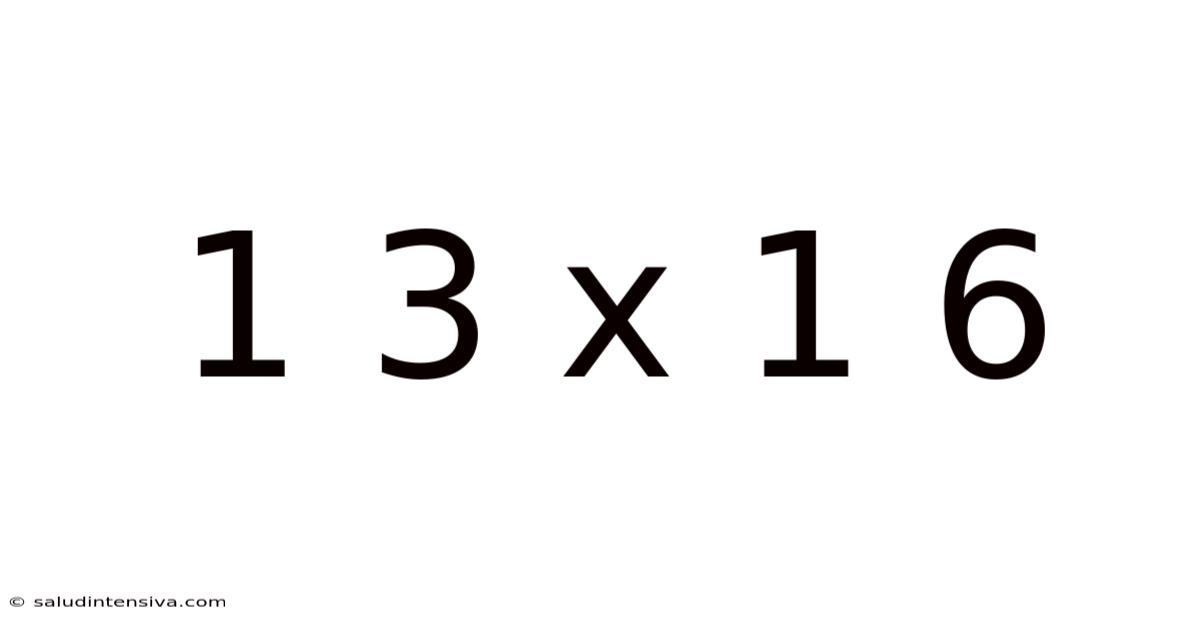
Table of Contents
Decoding 1, 3 x 1, 6: A Deep Dive into Mathematical Concepts and Applications
This article explores the seemingly simple expression "1, 3 x 1, 6," delving into its various interpretations, underlying mathematical principles, and practical applications across different fields. While the expression itself might appear basic, its analysis unveils a rich tapestry of mathematical concepts crucial for understanding more complex problems. We will examine different interpretations of the comma and multiplication symbol, explore the concepts of significant figures, rounding, and estimation, and discuss the relevance of this expression in real-world scenarios. This comprehensive guide will benefit students, educators, and anyone curious about the hidden depths of simple arithmetic.
Understanding the Expression: Interpretations and Ambiguities
The expression "1, 3 x 1, 6" presents an immediate challenge due to the use of commas as decimal separators. In many parts of the world, including Europe and parts of Asia, the comma (,) is used as the decimal separator, while the period (.) is used as the thousands separator. Conversely, in the United States and other countries, the period (.) acts as the decimal separator, and the comma (,) is used as the thousands separator.
This difference in notation significantly impacts the interpretation of the given expression. Let's analyze the two most likely scenarios:
Scenario 1: Comma as a Decimal Separator
If we assume the comma acts as a decimal separator, the expression becomes: 1.3 x 1.6
This represents a straightforward multiplication problem. The solution is obtained by multiplying 1.3 by 1.6:
1.3 x 1.6 = 2.08
Scenario 2: Comma as a Thousands Separator (Less Likely but Important to Address)
Although less probable given the context, we should briefly consider the possibility of the comma being a thousands separator. In this case, the numbers would be interpreted as 1003 and 1006. The multiplication would then be:
1003 x 1006 = 1009018
Significance of Significant Figures and Rounding
Regardless of the interpretation (decimal separator or thousands separator), the concept of significant figures becomes relevant. Significant figures represent the number of digits that carry meaning contributing to its measurement resolution. The accuracy of a calculation is limited by the least precise number involved.
In Scenario 1 (1.3 x 1.6), both numbers have two significant figures. The result, 2.08, should ideally also be presented with two significant figures. However, in this case, all digits are significant.
In Scenario 2 (1003 x 1006), both numbers have four significant figures. Therefore, the result, 1,009,018, also has four significant figures, although it might be rounded depending on the context of the calculation.
Estimation and Mental Math Techniques
The ability to estimate answers is a valuable skill in mathematics. Before performing the calculation, we can quickly estimate the product of 1.3 and 1.6. Rounding 1.3 to 1 and 1.6 to 2 gives us an estimate of 2. This confirms that our calculated answer of 2.08 is reasonable.
Similarly, in Scenario 2, we can estimate the product of 1003 and 1006 by rounding them to 1000. This gives us an estimate of 1,000,000, which provides a rough check on the accuracy of the precise calculation. Such estimation techniques are crucial for error detection and building numerical intuition.
Practical Applications: Real-World Examples
The simple multiplication represented by "1, 3 x 1, 6" (interpreting the comma as a decimal) finds applications in various real-world situations:
-
Unit Conversions: Converting units often involves multiplication. For example, if 1.3 meters is equivalent to 1.6 yards, then multiplying 1.3 by a conversion factor might yield a result similar to our example.
-
Calculating Areas: If you have a rectangular area with dimensions of 1.3 meters and 1.6 meters, the total area is calculated using the same multiplication.
-
Financial Calculations: Simple interest calculations, determining the cost of goods, or calculating discounts often involve similar multiplications. For instance, if an item costs 1.3 units of currency and you buy 1.6 units of the item, the total cost is easily obtained.
-
Scientific Measurements: In many scientific experiments, measurements are often obtained in decimal form, leading to similar multiplication operations to determine the result.
Beyond Basic Arithmetic: Extending the Concepts
While "1, 3 x 1, 6" appears basic, its analysis lays the groundwork for understanding more advanced mathematical concepts.
-
Algebra: The expression can be generalized algebraically. Instead of specific numbers, we can use variables: a x b. This opens up the world of algebraic manipulation and solving equations.
-
Calculus: Derivatives and integrals, fundamental concepts in calculus, build upon basic arithmetic operations. Understanding multiplication is crucial for mastering these advanced techniques.
-
Linear Algebra: Matrices and vectors, which are central to linear algebra, involve numerous multiplication operations.
Frequently Asked Questions (FAQ)
Q: What is the most common interpretation of the comma in "1, 3 x 1, 6"?
A: The most common interpretation depends on the region. In many European and Asian countries, the comma is the decimal separator, making it 1.3 x 1.6. However, in the USA and many other countries, it would be interpreted as a thousands separator, a less likely scenario in this context.
Q: Why is understanding significant figures important?
A: Significant figures indicate the precision of a measurement or calculation. Using the correct number of significant figures ensures that the results are not presented with a false sense of accuracy.
Q: How can I improve my estimation skills?
A: Practice regular estimation exercises. Try to round numbers to the nearest whole number or a simple multiple of 10 before performing calculations.
Conclusion: The Power of Simple Arithmetic
Although "1, 3 x 1, 6" appears to be a simple expression, its exploration unlocks a deeper understanding of crucial mathematical concepts such as decimal notation, significant figures, estimation techniques, and the practical applications of basic arithmetic in various fields. Mastering these foundational elements is vital for progressing to more complex mathematical concepts and successfully tackling real-world problems. The seemingly simple act of multiplication showcases the power and elegance of mathematics, highlighting its inherent ability to connect seemingly disparate areas of knowledge and experience. The journey from a simple arithmetic problem to a broader exploration of mathematical principles reinforces the idea that even the most basic elements can unlock significant insights and enhance our understanding of the world around us.
Latest Posts
Latest Posts
-
4 To The Third Power
Sep 19, 2025
-
1 10 In Decimal Form
Sep 19, 2025
-
120 Days From May 1
Sep 19, 2025
-
Convert 62 F To C
Sep 19, 2025
-
600 Square Feet Room Size
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.