1 4 In Simplest Form
saludintensiva
Sep 15, 2025 · 6 min read
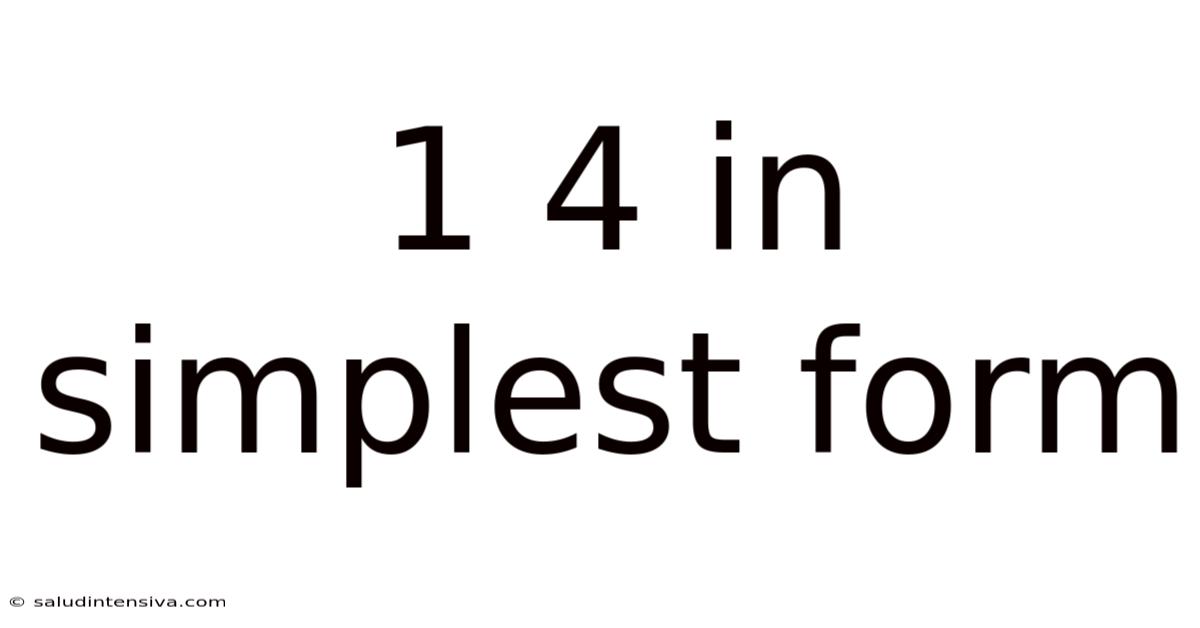
Table of Contents
Simplifying Fractions: A Deep Dive into 1/4
Understanding fractions is a cornerstone of mathematical literacy, crucial for everything from baking a cake to understanding complex financial concepts. This article provides a comprehensive guide to simplifying fractions, focusing specifically on the fraction 1/4. We'll explore what it means to simplify, delve into the mathematical principles behind it, and address common questions and misconceptions surrounding this seemingly simple concept. This guide is designed for learners of all levels, from those just beginning to explore fractions to those looking for a more in-depth understanding.
Understanding Fractions: The Building Blocks
Before we dive into simplifying 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many parts we have, while the denominator tells us how many equal parts the whole is divided into. For example, in the fraction 1/4, the numerator is 1 and the denominator is 4. This means we have 1 part out of a total of 4 equal parts.
What Does it Mean to Simplify a Fraction?
Simplifying a fraction, also known as reducing a fraction, means expressing it in its lowest terms. This means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. In essence, we're finding the simplest way to represent the same portion of the whole. Think of it like reducing a recipe – you can use the same proportions of ingredients even if you halve or double the recipe size.
Why Simplify Fractions?
Simplifying fractions is important for several reasons:
-
Clarity and Understanding: Simplified fractions are easier to understand and work with. Instead of dealing with a complex fraction like 12/16, it's much simpler to work with its simplified equivalent, 3/4.
-
Accuracy in Calculations: Simplifying fractions before performing operations like addition, subtraction, multiplication, or division can make calculations significantly easier and reduce the likelihood of errors.
-
Standardized Representation: Simplifying fractions ensures that everyone is working with the same, most efficient representation of a particular portion.
Simplifying 1/4: A Step-by-Step Guide
The fraction 1/4 is already in its simplest form. Let's understand why.
To simplify a fraction, we need to find the greatest common divisor (GCD) or greatest common factor (GCF) of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In the case of 1/4:
- The factors of 1 are only 1.
- The factors of 4 are 1, 2, and 4.
The only common factor between 1 and 4 is 1. Since the only common factor is 1, the fraction is already in its simplest form. We cannot divide both the numerator and denominator by any number greater than 1 to obtain a smaller, equivalent fraction. Therefore, 1/4 is considered a simplified fraction.
Visualizing 1/4
Visual representations can help solidify the understanding of fractions. Imagine a pizza cut into 4 equal slices. The fraction 1/4 represents one of those slices. You cannot divide that single slice into any smaller, equal parts while maintaining the same whole pizza representation. This visually confirms that 1/4 is already in its simplest form.
The Mathematical Principle Behind Simplification
The process of simplifying fractions relies on the fundamental principle of equivalent fractions. We can multiply or divide both the numerator and denominator of a fraction by the same non-zero number without changing the value of the fraction. This is because we're essentially multiplying or dividing by 1 (e.g., 2/2 = 1, 3/3 = 1).
To simplify, we divide both the numerator and denominator by their greatest common divisor (GCD). Since the GCD of 1 and 4 is 1, dividing both by 1 doesn't change the fraction's value; it remains 1/4.
Examples of Simplifying Other Fractions
Let's contrast simplifying 1/4 with examples of fractions that can be simplified:
-
12/16: The GCD of 12 and 16 is 4. Dividing both by 4 gives us 3/4.
-
6/9: The GCD of 6 and 9 is 3. Dividing both by 3 gives us 2/3.
-
25/100: The GCD of 25 and 100 is 25. Dividing both by 25 gives us 1/4 (notice this simplifies to the same simplified fraction as our initial example!).
These examples demonstrate the process of finding the GCD and using it to simplify the fraction to its lowest terms.
Common Mistakes and Misconceptions
A common mistake is to incorrectly identify the GCD or to forget to divide both the numerator and denominator by the same number. Always remember that the operation must be applied consistently to both parts of the fraction to maintain its value. Another misconception is believing that only fractions with even numbers can be simplified. As the examples show, fractions with odd numbers can also be simplified if they share a common factor other than 1.
Frequently Asked Questions (FAQ)
Q1: Can a fraction be simplified if the numerator is 1?
A1: Not always. If the numerator is 1, the fraction can only be simplified if the denominator is also 1 (resulting in 1/1 = 1). Otherwise, as in the case of 1/4, it's already in its simplest form.
Q2: What if the GCD is 1?
A2: If the GCD of the numerator and denominator is 1, then the fraction is already in its simplest form and cannot be simplified further.
Q3: Is it necessary to simplify every fraction?
A3: While not always strictly necessary, simplifying fractions improves clarity, accuracy, and makes further calculations easier. It's generally good practice to simplify whenever possible.
Q4: How can I find the GCD quickly?
A4: There are several methods for finding the GCD, including listing factors, using prime factorization, or using the Euclidean algorithm (a more advanced method). For smaller numbers, listing factors is often the easiest approach.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics. While the fraction 1/4 is already in its simplest form, understanding the principles behind simplification is crucial for working with other fractions. By mastering the techniques discussed, you’ll be well-equipped to handle various fraction-related problems with confidence and accuracy, laying a strong foundation for more advanced mathematical concepts. Remember the key principle: find the greatest common divisor and divide both the numerator and the denominator by it to reach the simplest form. Practice is key – the more you work with fractions, the more intuitive the process will become.
Latest Posts
Latest Posts
-
Is 9 Prime Or Composite
Sep 15, 2025
-
15 20 As A Percent
Sep 15, 2025
-
All The Factors Of 24
Sep 15, 2025
-
Is 1 3 Bigger Than 1 4
Sep 15, 2025
-
Is 1 8 Bigger Than 1 2
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 4 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.