1/4 On A Number Line
saludintensiva
Sep 21, 2025 · 6 min read
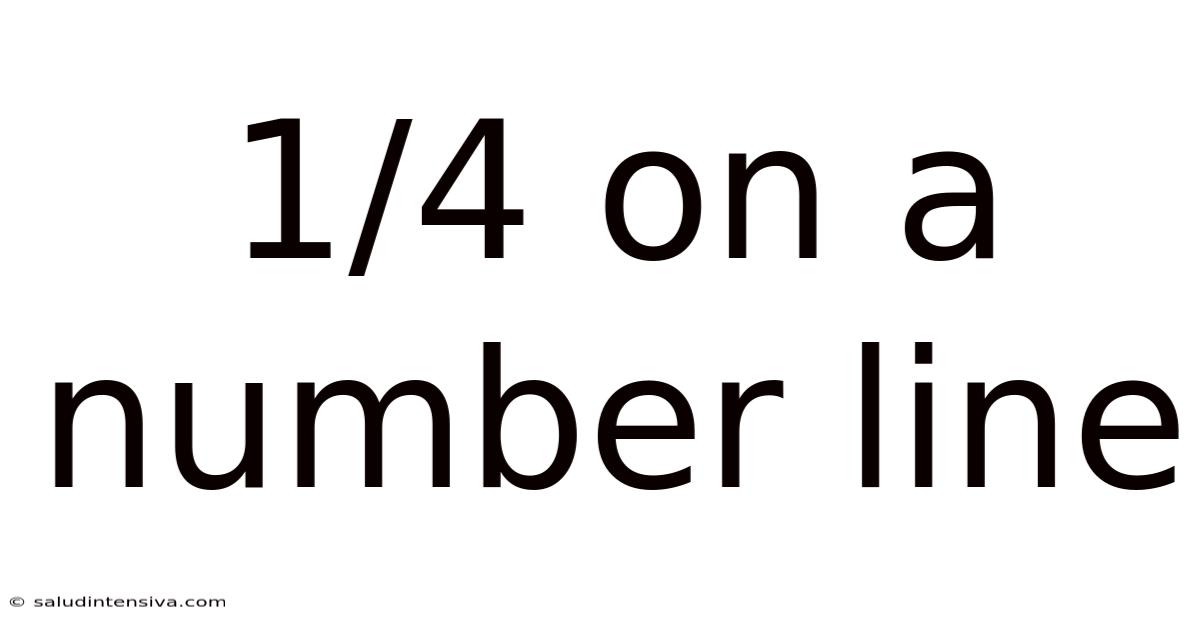
Table of Contents
Understanding 1/4 on the Number Line: A Comprehensive Guide
Understanding fractions, especially their representation on a number line, is a fundamental concept in mathematics. This comprehensive guide delves into the meaning of 1/4 (one-quarter) on a number line, exploring its representation, practical applications, and related concepts. We'll move beyond simple visualization and explore deeper mathematical implications, ensuring a thorough understanding for learners of all levels.
What is a Number Line?
Before we dive into 1/4, let's establish a solid understanding of the number line itself. A number line is a visual representation of numbers as points on a line. It extends infinitely in both positive and negative directions, with zero positioned at the center. The numbers are spaced evenly along the line, with positive numbers to the right of zero and negative numbers to the left. This simple tool is crucial for understanding number relationships, comparisons, and operations.
Representing 1/4 on the Number Line
1/4, or one-quarter, represents one part out of four equal parts of a whole. To represent this on a number line, we need to divide the space between 0 and 1 into four equal segments. Each segment will then represent 1/4.
-
Step 1: Mark 0 and 1: Begin by marking the points 0 and 1 on your number line. This represents the whole unit we're working with.
-
Step 2: Divide into Four Equal Parts: Divide the space between 0 and 1 into four equal parts. You can achieve this by visually estimating or using a ruler for precise measurements.
-
Step 3: Mark 1/4, 2/4, 3/4: Mark each division point. The first division point to the right of 0 represents 1/4. The second represents 2/4 (which simplifies to 1/2), and the third represents 3/4. The fourth point is, of course, 1 (or 4/4).
-
Visual Representation: Your number line should now clearly show 0, 1/4, 1/2 (2/4), 3/4, and 1. This visually demonstrates the position of 1/4 within the whole unit.
Beyond the Basic Representation: Extending the Concept
While representing 1/4 between 0 and 1 is straightforward, the concept extends to larger numbers and negative numbers.
-
Representing 1 1/4: To represent 1 1/4 (one and one-quarter), you would follow the same steps as above, but then extend the number line beyond 1. 1 1/4 would be located one full unit to the right of 0, and then an additional 1/4 of a unit further.
-
Representing -1/4: To represent -1/4 (negative one-quarter), you would simply mirror the process on the left side of zero. -1/4 would be the first mark to the left of 0.
-
Representing Fractions Larger than 1: Consider a fraction like 5/4 (five-quarters). This is equivalent to 1 1/4. You'd locate it 1 and 1/4 units to the right of zero. This demonstrates the relationship between improper fractions and mixed numbers.
Practical Applications of Understanding 1/4 on a Number Line
Understanding the placement of 1/4 on a number line has many practical applications beyond the classroom:
-
Measurement: Imagine measuring ingredients for a recipe. If a recipe calls for 1/4 cup of sugar, you can visually represent this on a measuring cup by understanding that it's one of four equal parts.
-
Time: A quarter of an hour is 15 minutes. You can represent this on a clock face or a timeline.
-
Data Representation: Graphs and charts frequently utilize fractions to represent data. Understanding 1/4's position on a number line allows you to interpret and analyze this data more effectively.
-
Money: A quarter (25 cents) is 1/4 of a dollar. Understanding this relationship is crucial for financial literacy.
-
Geometry: Dividing shapes into quarters requires understanding the concept of 1/4.
The Mathematical Significance of 1/4
1/4 is not just a simple fraction; it holds significant mathematical importance:
-
Decimal Equivalent: 1/4 is equivalent to 0.25. This demonstrates the connection between fractions and decimals. On the number line, 0.25 would occupy the same position as 1/4.
-
Percentage Equivalent: 1/4 is equivalent to 25%. This highlights the relationship between fractions, decimals, and percentages – all crucial for various mathematical applications.
-
Relationship to Other Fractions: Understanding 1/4 facilitates understanding other fractions. For instance, 1/2 is twice as large as 1/4, and 3/4 is three times as large.
Comparing and Ordering Fractions using the Number Line
The number line offers a powerful visual tool for comparing and ordering fractions. By placing fractions on the line, you can easily see which fraction is larger or smaller. For example, you can instantly see that 3/4 is greater than 1/4, and 1/2 lies exactly in the middle.
Connecting 1/4 to Other Mathematical Concepts
Understanding 1/4 forms a foundation for understanding more complex mathematical concepts:
-
Proportions: 1/4 is a fundamental part of understanding proportions and ratios. For example, if 1/4 of a group of 20 people are wearing blue shirts, you can easily calculate how many people are wearing blue shirts (5).
-
Probability: In probability, 1/4 represents a 25% chance of an event occurring.
-
Algebra: Fractions are integral to algebraic equations and manipulations. Understanding 1/4 strengthens your foundation for working with more complex algebraic expressions.
Frequently Asked Questions (FAQ)
Q: Can 1/4 be represented on a number line other than the one between 0 and 1?
A: Absolutely! You can represent 1/4 on any number line by dividing the relevant section into four equal parts. For example, you could represent it on the number line between 2 and 3 by dividing the space between them into four equal parts.
Q: What if I don't have a ruler to divide the line precisely?
A: While precise measurement is ideal, a reasonable visual estimate is perfectly acceptable, particularly for understanding the concept.
Q: Is there only one way to represent 1/4 on a number line?
A: While the standard representation is between 0 and 1, there are infinite ways to represent 1/4, depending on the scale of the number line.
Q: How can I use the number line to add or subtract fractions like 1/4?
A: The number line is a great tool for visualizing addition and subtraction of fractions. To add 1/4 and 1/4, start at 1/4 on the line and move another 1/4 to the right, landing at 1/2. Subtraction works similarly, moving to the left.
Q: Why is understanding 1/4 important in real-world scenarios?
A: Understanding 1/4 is crucial for tasks involving measurement, time management, financial calculations, and data interpretation. It’s a fundamental skill that enhances problem-solving abilities in various fields.
Conclusion
Understanding 1/4 on a number line is a foundational element of mathematical literacy. This seemingly simple concept unlocks a deeper understanding of fractions, decimals, percentages, and their numerous practical applications. By mastering the representation and application of 1/4 on a number line, you build a strong base for tackling more complex mathematical problems and real-world challenges. The visual nature of the number line makes this concept accessible and engaging, making it a crucial tool for learning and applying mathematical concepts effectively. Remember, the key is to practice and visualize; the more you work with the number line, the more intuitive and clear this concept will become.
Latest Posts
Latest Posts
-
3 2 4 2 3 4
Sep 21, 2025
-
7 16 Inches To Decimal
Sep 21, 2025
-
Inches To Decimal Feet Chart
Sep 21, 2025
-
8 12 In Lowest Terms
Sep 21, 2025
-
Subtract Days From Date Javascript
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1/4 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.