1 40 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
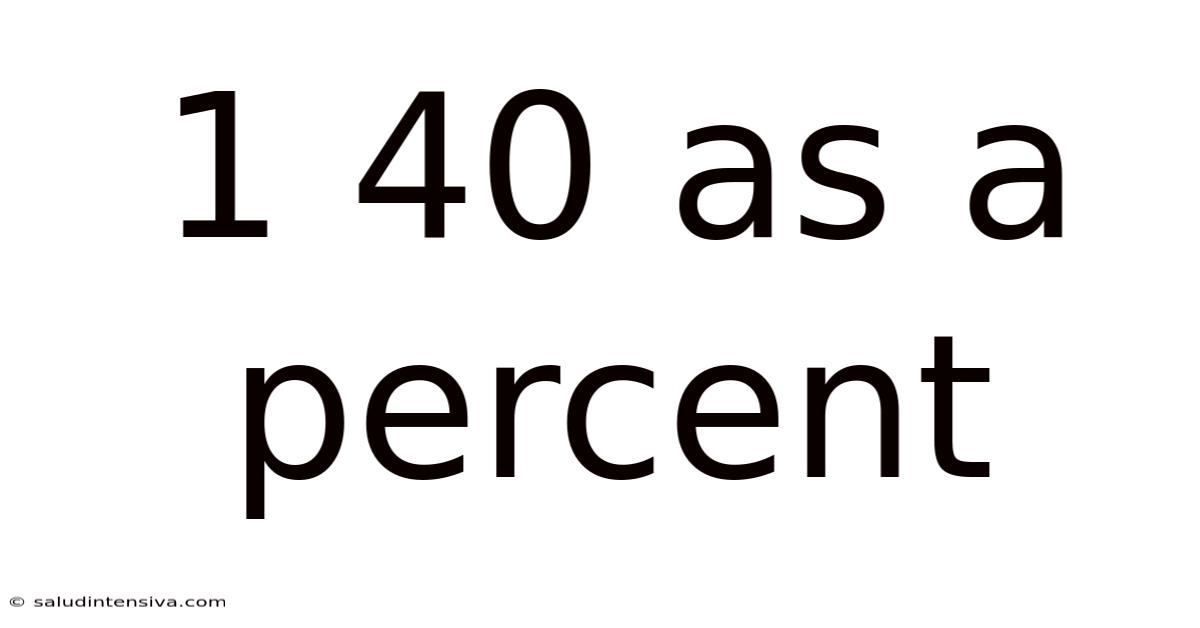
Table of Contents
Understanding 1/40 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts to understanding financial reports. This article delves deep into converting the fraction 1/40 into a percentage, explaining the process step-by-step, providing real-world examples, and addressing common queries. We'll explore the underlying mathematical principles and offer practical strategies to master this essential conversion. By the end, you'll not only know the percentage equivalent of 1/40 but also have a solid grasp of the broader concepts involved.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specifics of 1/40, let's establish the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 1/40 means one part out of forty equal parts.
-
Decimals: Represent a part of a whole using base-ten notation. They are essentially fractions where the denominator is a power of 10 (10, 100, 1000, etc.).
-
Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" signifies "per hundred." So, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
These three representations are interchangeable, allowing for flexibility in calculations and interpretations. The ability to convert between them is crucial for problem-solving in numerous contexts.
Converting 1/40 to a Percentage: A Step-by-Step Guide
There are two primary methods to convert the fraction 1/40 into a percentage:
Method 1: Using Decimal Conversion
This method involves first converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
-
Divide the numerator by the denominator: 1 ÷ 40 = 0.025
-
Multiply the decimal by 100: 0.025 × 100 = 2.5
-
Add the percentage symbol: 2.5%
Therefore, 1/40 is equal to 2.5%.
Method 2: Direct Proportion
This method leverages the definition of percentage as a fraction of 100. We set up a proportion:
1/40 = x/100
Where 'x' represents the percentage we want to find.
To solve for 'x', we cross-multiply:
40x = 100
x = 100 ÷ 40
x = 2.5
Therefore, 1/40 is equal to 2.5%. This method highlights the fundamental relationship between fractions and percentages.
Real-World Applications of 1/40 as a Percentage
Understanding that 1/40 equals 2.5% allows for practical application in various scenarios:
-
Discounts: A store offering a 2.5% discount on an item is essentially offering a reduction equivalent to 1/40 of the original price.
-
Tax Calculations: If a sales tax is 2.5%, it means you'll pay an additional amount equal to 1/40 of the item's pre-tax price.
-
Statistical Analysis: In data analysis, a 2.5% occurrence rate can be represented as a fraction of 1/40.
-
Financial Investments: Understanding percentage returns on investments is crucial, and converting fractional returns (like 1/40) to percentages provides a clear understanding of the growth or loss.
-
Measurement and Proportion: In construction, engineering, or any field dealing with precise measurements, understanding fractions and percentages is essential for scaling and accurate calculations. A 2.5% error in a measurement, for example, could be equivalent to 1/40 of the total measurement.
Beyond the Basics: Working with More Complex Fractions and Percentages
While this article focuses on 1/40, the principles discussed are applicable to a wide range of fractions and percentage conversions. Understanding the core concepts—division, proportion, and the relationship between fractions, decimals, and percentages—empowers you to tackle more complex scenarios. For example:
-
Converting larger fractions: To convert a fraction like 3/8 to a percentage, you would follow the same steps: 3 ÷ 8 = 0.375, then 0.375 × 100 = 37.5%.
-
Converting percentages to fractions: To convert a percentage like 60% to a fraction, you would express it as 60/100, and then simplify it to 3/5.
-
Working with mixed numbers: If you encounter mixed numbers (like 2 1/4), you would first convert them to improper fractions (9/4 in this example) before proceeding with the percentage conversion.
Frequently Asked Questions (FAQ)
Q: Why is understanding percentage conversion important?
A: Percentage conversion is crucial for numerous applications in everyday life and professional settings, allowing for easier comparison and understanding of proportions, rates, and changes in various quantities.
Q: Are there any shortcuts for converting fractions to percentages?
A: While the methods described offer clarity and understanding, certain fractions (like those with denominators that are factors of 100) allow for quicker mental calculations. For instance, 1/2 is 50%, 1/4 is 25%, and 1/10 is 10%. However, for most fractions, the systematic approach (decimal conversion or proportion) ensures accuracy.
Q: What if the resulting percentage has a long decimal?
A: In such cases, you can round the percentage to a desired level of precision (e.g., rounding to one or two decimal places). The context of the problem will dictate the appropriate level of rounding.
Q: Can I use a calculator for these conversions?
A: Absolutely! Calculators are helpful tools for performing the necessary divisions and multiplications, making the process faster and reducing the risk of calculation errors, especially with more complex fractions.
Q: How can I improve my skills in fraction and percentage conversions?
A: Practice is key! Work through various examples, starting with simple fractions and gradually progressing to more challenging ones. Online resources, textbooks, and practice exercises can significantly improve your understanding and proficiency.
Conclusion: Mastering the Art of Percentage Conversion
Converting 1/40 to a percentage—which is 2.5%—is a fundamental skill within a broader understanding of fractions, decimals, and percentages. This seemingly simple conversion unlocks a wealth of practical applications across various disciplines. By grasping the underlying mathematical principles and practicing the conversion methods, you'll develop a valuable skill that enhances your numeracy and problem-solving abilities. Remember, the ability to seamlessly navigate between these different numerical representations empowers you to analyze data, interpret information, and confidently tackle challenges in both academic and real-world scenarios. So, embrace the power of percentages and unlock a deeper understanding of the mathematical world around you.
Latest Posts
Latest Posts
-
Ft Per Min To Mph
Sep 14, 2025
-
Whats The Factors Of 18
Sep 14, 2025
-
51 Degree Fahrenheit To Celsius
Sep 14, 2025
-
1 3 5 As A Decimal
Sep 14, 2025
-
Is 24 A Prime Number
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 40 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.