1 50 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
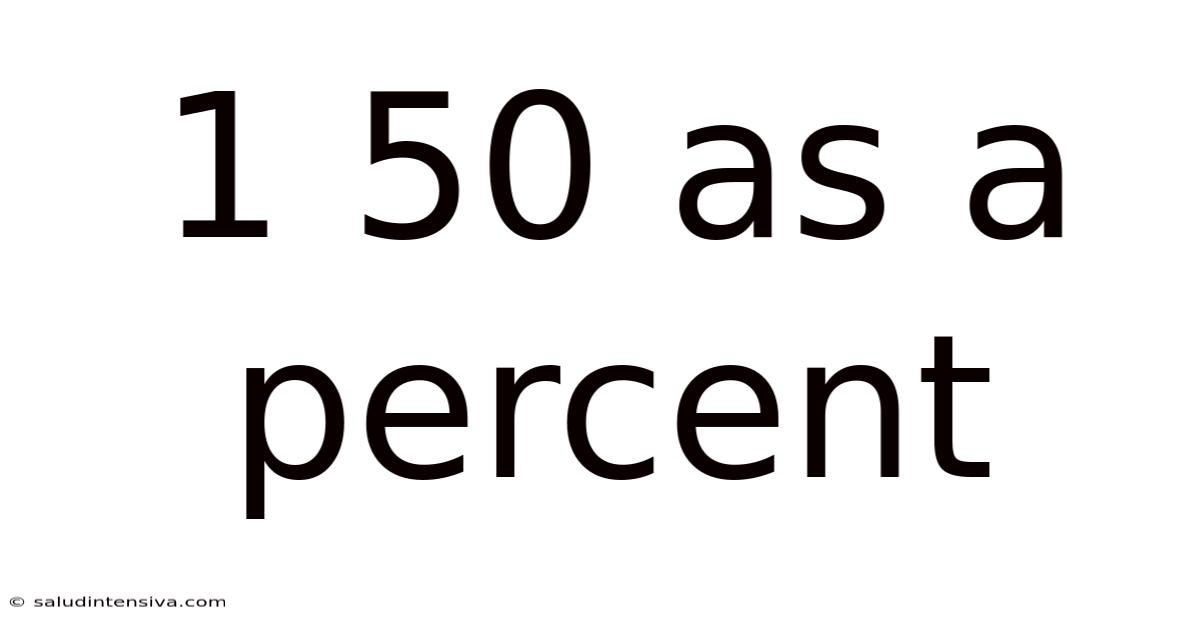
Table of Contents
1/50 as a Percent: Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This article will comprehensively explore how to convert the fraction 1/50 into a percentage, explaining the process step-by-step and providing additional context to solidify your understanding of these core mathematical concepts. We'll cover the underlying principles, offer practical examples, and answer frequently asked questions to ensure a thorough grasp of the topic. This will not only help you understand 1/50 as a percentage but also equip you with the skills to convert any fraction into a percentage.
Introduction: Fractions, Decimals, and Percentages – A Unified Concept
Before diving into the specific conversion of 1/50, let's establish a clear understanding of the interconnectedness of fractions, decimals, and percentages. They all represent parts of a whole, just expressed differently.
-
Fractions: Represent a part of a whole using a numerator (top number) and a denominator (bottom number). The numerator indicates the number of parts, and the denominator indicates the total number of equal parts. For example, 1/50 means one part out of fifty equal parts.
-
Decimals: Represent a part of a whole using the base-ten number system. The position of the digits after the decimal point indicates the value – tenths, hundredths, thousandths, and so on.
-
Percentages: Represent a part of a whole as a fraction of 100. The percentage symbol (%) indicates that the number is a fraction out of 100. For example, 50% means 50 parts out of 100.
The ability to convert between these representations is crucial for problem-solving in various contexts, from calculating discounts to understanding financial data.
Converting 1/50 to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To do this, we simply divide the numerator (1) by the denominator (50):
1 ÷ 50 = 0.02
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.02 x 100 = 2%
Therefore, 1/50 is equal to 2%.
Alternative Method: Using Equivalent Fractions
Another way to approach this conversion is by finding an equivalent fraction with a denominator of 100. This method is particularly useful when working with fractions that have denominators that are easily scaled to 100. While not as straightforward for 1/50, understanding this method provides a broader understanding of fraction manipulation.
To find an equivalent fraction with a denominator of 100, we need to determine what number we must multiply the denominator (50) by to obtain 100. In this case, it's 2 (50 x 2 = 100). Crucially, we must multiply both the numerator and the denominator by the same number to maintain the value of the fraction:
(1 x 2) / (50 x 2) = 2/100
Since a percentage represents parts per hundred, 2/100 directly translates to 2%.
Illustrative Examples: Applying the Conversion in Real-World Scenarios
Let's look at how understanding the conversion of 1/50 to 2% can be applied in practical situations:
Example 1: Discount Calculation
A store offers a discount of 1/50 on all items. This means a 2% discount. If an item costs $100, the discount amount is $100 x 0.02 = $2. The final price would be $100 - $2 = $98.
Example 2: Survey Results
In a survey of 50 people, one person answered "yes" to a particular question. The proportion of "yes" answers can be represented as 1/50, or 2%.
Example 3: Probability
If there's a 1/50 chance of winning a lottery, that translates to a 2% probability of winning.
These examples highlight the practical utility of converting fractions to percentages for everyday calculations and interpretations.
Further Exploration: Understanding Percentages Greater Than 100%
While the conversion of 1/50 resulted in a percentage less than 100%, it's important to note that percentages can also be greater than 100%. This occurs when the numerator of the fraction is larger than the denominator. For example, if you have a fraction like 3/2, the decimal equivalent is 1.5, which converts to 150%. This simply means you have 150% of the original quantity, or 1 and a half times the original quantity.
Frequently Asked Questions (FAQ)
Q1: Why do we multiply by 100 to convert a decimal to a percentage?
A1: A percentage is a fraction expressed out of 100. Multiplying a decimal by 100 effectively converts it into a fraction with a denominator of 100.
Q2: Can I convert any fraction to a percentage?
A2: Yes, any fraction can be converted to a percentage by following the steps outlined above: divide the numerator by the denominator to get a decimal, then multiply by 100 and add the % symbol.
Q3: What if the decimal has many digits after the decimal point?
A3: You can round the decimal to a certain number of decimal places for practical purposes. The level of precision required will depend on the context of the problem. For example, you might round to two decimal places for financial calculations.
Q4: Are there any online tools or calculators to convert fractions to percentages?
A4: Yes, many online calculators are available that can perform this conversion quickly and easily. However, understanding the underlying process is more valuable than relying solely on calculators.
Q5: What's the difference between a percentage and a proportion?
A5: A proportion is a ratio of two quantities, often expressed as a fraction. A percentage is a specific type of proportion that expresses the ratio as a fraction of 100. So, a percentage is a specific form of a proportion.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting fractions to percentages is a fundamental skill with broad applications across various fields. Understanding the underlying principles, as demonstrated with the conversion of 1/50 to 2%, empowers you to confidently tackle more complex problems involving fractions, decimals, and percentages. By mastering this skill, you'll enhance your mathematical proficiency and improve your ability to analyze and interpret data presented in various formats. Remember to practice the steps involved, and don't hesitate to explore additional resources and examples to further solidify your understanding. The ability to seamlessly move between these three representations is a key component of mathematical fluency and practical problem-solving.
Latest Posts
Latest Posts
-
0 34 Acres To Sq Ft
Sep 15, 2025
-
Whats 8 As A Fraction
Sep 15, 2025
-
3 To The 6 Power
Sep 15, 2025
-
What Is 6 9 Reduced
Sep 15, 2025
-
What Time Is 20 45
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.