1/8 Is Greater Than 1/6
saludintensiva
Sep 10, 2025 · 6 min read
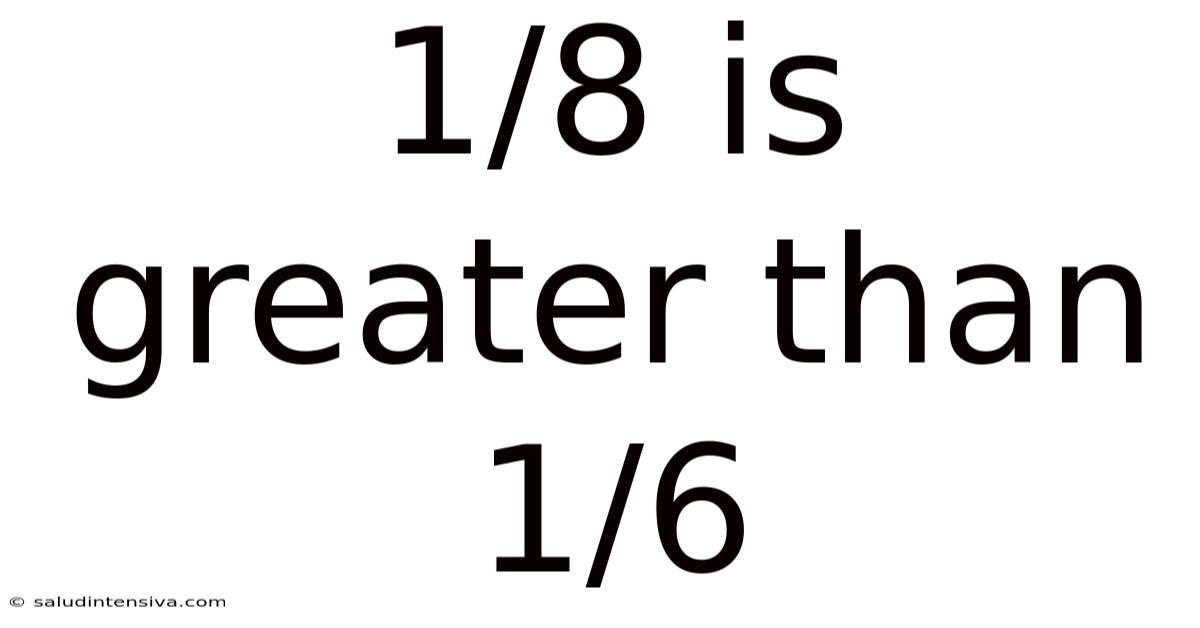
Table of Contents
Is 1/8 Greater Than 1/6? Understanding Fractions and Their Comparisons
Understanding fractions can sometimes feel like navigating a maze. Many people struggle with comparing fractions, especially when the numerators (the top numbers) are the same or when the denominators (the bottom numbers) are different. This article will delve into the comparison of 1/8 and 1/6, explaining why one is larger than the other and providing a solid foundation for understanding fraction comparisons in general. We’ll explore various methods to solve this problem, address common misconceptions, and provide you with the tools to confidently tackle similar comparisons in the future.
Introduction: Deconstructing the Question
The statement "1/8 is greater than 1/6" is incorrect. 1/6 is actually greater than 1/8. This might seem counterintuitive at first glance, especially if you're only focusing on the denominators. Let's explore why this is the case by examining the concept of fractions and the different methods for comparing them.
Visualizing Fractions: The Pizza Analogy
A helpful way to grasp the concept of fractions is to imagine a pizza. If you divide the pizza into 6 equal slices (1/6), each slice will be larger than if you divide the same-sized pizza into 8 equal slices (1/8). The more slices you have, the smaller each individual slice becomes. Therefore, one slice out of six (1/6) is larger than one slice out of eight (1/8). This visual representation helps solidify the understanding that a smaller denominator represents larger pieces.
Method 1: Finding a Common Denominator
One of the most reliable methods for comparing fractions is to find a common denominator. This involves finding a number that both denominators can divide into evenly. For 1/6 and 1/8, the least common multiple (LCM) is 24.
- To convert 1/6 to an equivalent fraction with a denominator of 24, we multiply both the numerator and the denominator by 4: (1 x 4) / (6 x 4) = 4/24.
- Similarly, to convert 1/8 to an equivalent fraction with a denominator of 24, we multiply both the numerator and the denominator by 3: (1 x 3) / (8 x 3) = 3/24.
Now, comparing 4/24 and 3/24 is straightforward. Since 4 > 3, we can conclude that 4/24 (which is equivalent to 1/6) is greater than 3/24 (which is equivalent to 1/8). Therefore, 1/6 > 1/8.
Method 2: Using Decimals
Converting fractions to decimals provides another effective method for comparison. This method is particularly useful when dealing with more complex fractions.
- To convert 1/6 to a decimal, we divide the numerator (1) by the denominator (6): 1 ÷ 6 ≈ 0.1667
- To convert 1/8 to a decimal, we divide the numerator (1) by the denominator (8): 1 ÷ 8 = 0.125
By comparing the decimal equivalents, we see that 0.1667 > 0.125, confirming that 1/6 is greater than 1/8.
Method 3: Visual Representation on a Number Line
A number line can be a powerful visual tool for comparing fractions. Plotting both fractions on a number line clearly shows their relative positions. Since 1/6 is closer to 0.5 (or 1/2) than 1/8, it demonstrates that 1/6 is the larger fraction. This method enhances visual understanding and reinforces the concept of fraction magnitude.
Addressing Common Misconceptions
A frequent mistake is focusing solely on the denominators. Students might incorrectly assume that since 8 is larger than 6, 1/8 must be larger than 1/6. However, the denominator indicates the number of parts a whole is divided into, not the size of each part. A larger denominator means smaller parts, leading to a smaller overall fraction value if the numerator remains the same.
Another misconception is the belief that comparing fractions requires a complex calculation in every instance. While finding a common denominator or converting to decimals are reliable methods, understanding the fundamental relationship between the numerator and denominator can often lead to intuitive comparisons, especially with simpler fractions.
The Importance of Understanding Fraction Comparison
Mastering fraction comparison is crucial for success in mathematics and numerous related fields. It's a foundational skill that builds a strong base for more advanced mathematical concepts, including algebra, geometry, and calculus. Understanding fractions is also valuable in everyday life, from cooking and baking to measuring ingredients and understanding proportions.
Expanding on Fraction Concepts: Beyond Simple Comparisons
While this article focuses on comparing 1/8 and 1/6, the principles discussed apply to a broader range of fraction comparisons. Whether you’re comparing fractions with different numerators and denominators, or dealing with mixed numbers (whole numbers combined with fractions), the underlying concepts of common denominators, decimal conversion, and visual representation remain essential tools.
Practical Applications: Real-World Examples
Let’s look at a couple of real-world examples where understanding fraction comparison is key:
- Baking: A recipe calls for 1/6 cup of sugar in one version and 1/8 cup in another. Knowing that 1/6 > 1/8, you can easily determine which recipe requires more sugar.
- Construction: Comparing the lengths of materials using fractions. A carpenter might need to choose between two pieces of wood, one measuring 1/6 of a foot and the other 1/8 of a foot. Understanding which is longer is vital for selecting the appropriate material.
Frequently Asked Questions (FAQ)
Q: Why can't I just compare the denominators directly?
A: Comparing only the denominators is misleading because the denominator represents the number of equal parts a whole is divided into, not the size of each part. A larger denominator indicates more, smaller parts.
Q: Is there a quick way to compare fractions without calculations?
A: For simple fractions like 1/6 and 1/8, visualizing them as parts of a whole (like the pizza example) can provide a quick, intuitive comparison.
Q: What if the fractions have different numerators?
A: For fractions with different numerators and denominators, finding a common denominator or converting to decimals remains the most reliable methods for comparison.
Q: Are there any other methods for comparing fractions?
A: Yes, using cross-multiplication is another effective method. To compare a/b and c/d, you cross-multiply: ad and bc. If ad > bc, then a/b > c/d.
Conclusion: Mastering Fraction Comparison
Understanding fraction comparison, particularly the difference between 1/6 and 1/8, is a fundamental skill with far-reaching applications. By mastering the methods described—finding common denominators, using decimal equivalents, and employing visual aids—you'll build a strong foundation in mathematics and enhance your ability to solve problems in various contexts. Remember, practice is key. The more you work with fractions, the more intuitive and comfortable you'll become with comparing their values. Don't hesitate to revisit these methods and use them to compare any fractions you encounter. With consistent effort, you'll confidently navigate the world of fractions and unlock their hidden potential.
Latest Posts
Latest Posts
-
Mega Millions Random Number Generator
Sep 10, 2025
-
14 3 As A Decimal
Sep 10, 2025
-
What Does 5 3 Equal
Sep 10, 2025
-
Excel Convert Time To Number
Sep 10, 2025
-
Fractions Equal To 5 8
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1/8 Is Greater Than 1/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.