1 8 Times 1 4
saludintensiva
Sep 15, 2025 · 6 min read
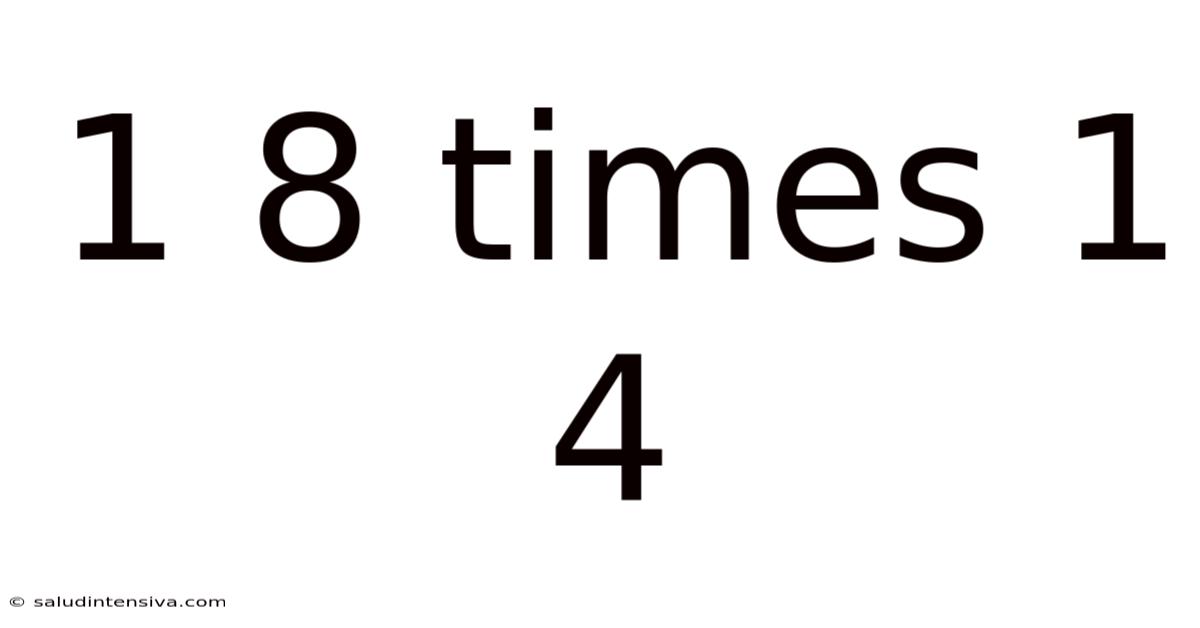
Table of Contents
Decoding 1/8 x 1/4: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a clear approach, it becomes surprisingly intuitive. This article will thoroughly explain how to multiply 1/8 by 1/4, covering the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. We'll break down the concept in a way that's accessible to everyone, regardless of their prior math experience. By the end, you'll not only know the answer to 1/8 x 1/4 but also possess a solid grasp of multiplying fractions in general.
Introduction: Understanding Fractions
Before diving into the multiplication, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/8, the numerator is 1 and the denominator is 8. This means we have 1 out of 8 equal parts of a whole.
Step-by-Step Multiplication of 1/8 x 1/4
The beauty of multiplying fractions lies in its simplicity. To multiply two fractions, we follow these straightforward steps:
-
Multiply the numerators: Multiply the top numbers of both fractions together. In our case, this is 1 x 1 = 1.
-
Multiply the denominators: Multiply the bottom numbers of both fractions together. In our case, this is 8 x 4 = 32.
-
Form the resulting fraction: Combine the results from steps 1 and 2 to form the new fraction. Therefore, 1/8 x 1/4 = 1/32.
So, the answer to 1/8 multiplied by 1/4 is 1/32.
Visualizing the Multiplication
It's often helpful to visualize fraction multiplication. Imagine a square divided into 8 equal columns (representing 1/8). Now, imagine dividing each of those columns into 4 equal rows (representing 1/4). This creates a total of 32 smaller squares (8 columns x 4 rows = 32 squares). The fraction 1/8 x 1/4 represents taking one of these 32 smaller squares, hence resulting in 1/32.
The Mathematical Principle Behind Fraction Multiplication
The process of multiplying fractions isn't just a set of arbitrary rules; it's rooted in the fundamental concept of repeated addition. Consider 3 x 1/4. This means we're adding 1/4 to itself three times: 1/4 + 1/4 + 1/4 = 3/4. Notice that we added the numerators while keeping the denominator consistent. In general, we're finding a portion of a portion.
When we multiply 1/8 x 1/4, we're essentially finding one-fourth of one-eighth. This means taking 1/4 of the 1/8 portion of the whole. The multiplication process efficiently calculates this portion of a portion.
Simplifying Fractions (If Necessary)
Sometimes, after multiplying fractions, the resulting fraction can be simplified. This means reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In the case of 1/32, both 1 and 32 are only divisible by 1, meaning the fraction is already in its simplest form.
Let's consider another example: 2/6 x 3/4.
- Multiply numerators: 2 x 3 = 6
- Multiply denominators: 6 x 4 = 24
- Resulting fraction: 6/24
Now, we simplify 6/24. The GCD of 6 and 24 is 6. Dividing both the numerator and denominator by 6, we get 1/4.
Multiplying Fractions with Whole Numbers
When multiplying a fraction by a whole number, remember that a whole number can be expressed as a fraction with a denominator of 1. For example, 5 can be written as 5/1. To multiply 5 by 1/2:
- Rewrite the whole number as a fraction: 5/1
- Multiply the numerators: 5 x 1 = 5
- Multiply the denominators: 1 x 2 = 2
- Resulting fraction: 5/2 (This can also be written as 2 1/2 or 2.5)
Multiplying Mixed Numbers
A mixed number consists of a whole number and a fraction (e.g., 2 1/3). Before multiplying mixed numbers, it's best to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator: For 2 1/3, this is 2 x 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: The denominator remains 3.
- Improper fraction: 7/3
Now you can multiply the improper fractions using the standard method.
Frequently Asked Questions (FAQs)
Q1: What if I have more than two fractions to multiply?
A: Simply multiply all the numerators together and all the denominators together. The order of multiplication doesn't matter due to the commutative property of multiplication.
Q2: Can I cancel out common factors before multiplying?
A: Yes! This technique, called cancellation, simplifies the calculation. Before multiplying, you can divide any numerator and any denominator by their greatest common divisor. For instance, in (2/6) x (3/4), you can divide 2 and 4 by 2, and 3 and 6 by 3, resulting in (1/2) x (1/2) = 1/4. This makes the calculation much easier.
Q3: Why is multiplying fractions different from adding or subtracting fractions?
A: Adding and subtracting fractions require a common denominator. This is because you are combining or comparing parts of the whole. Multiplication, however, deals with finding a portion of a portion, and a common denominator isn't necessary.
Q4: What are some real-world applications of fraction multiplication?
A: Fraction multiplication is used extensively in various fields. For example:
- Cooking: Scaling recipes up or down.
- Construction: Calculating material quantities.
- Finance: Determining percentages and proportions.
- Science: Measuring quantities and concentrations.
Conclusion: Mastering Fraction Multiplication
Multiplying fractions, even seemingly complex ones like 1/8 x 1/4, is a straightforward process once you understand the underlying principles. By following the step-by-step procedure, visualizing the process, and understanding the mathematical concepts, you can confidently tackle any fraction multiplication problem. Remember to simplify your answers to their lowest terms whenever possible. With practice, this skill will become second nature, empowering you to solve a wide range of mathematical problems and real-world applications. The seemingly simple equation, 1/8 x 1/4 = 1/32, opens the door to a deeper understanding of the fascinating world of fractions.
Latest Posts
Latest Posts
-
6 And 9 Common Multiples
Sep 15, 2025
-
10 25 As A Percent
Sep 15, 2025
-
340 Degrees Fahrenheit To Celsius
Sep 15, 2025
-
3 3 As A Decimal
Sep 15, 2025
-
Lcm Of 2 3 6
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1 8 Times 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.