1 Divided By 1 4
saludintensiva
Sep 19, 2025 · 5 min read
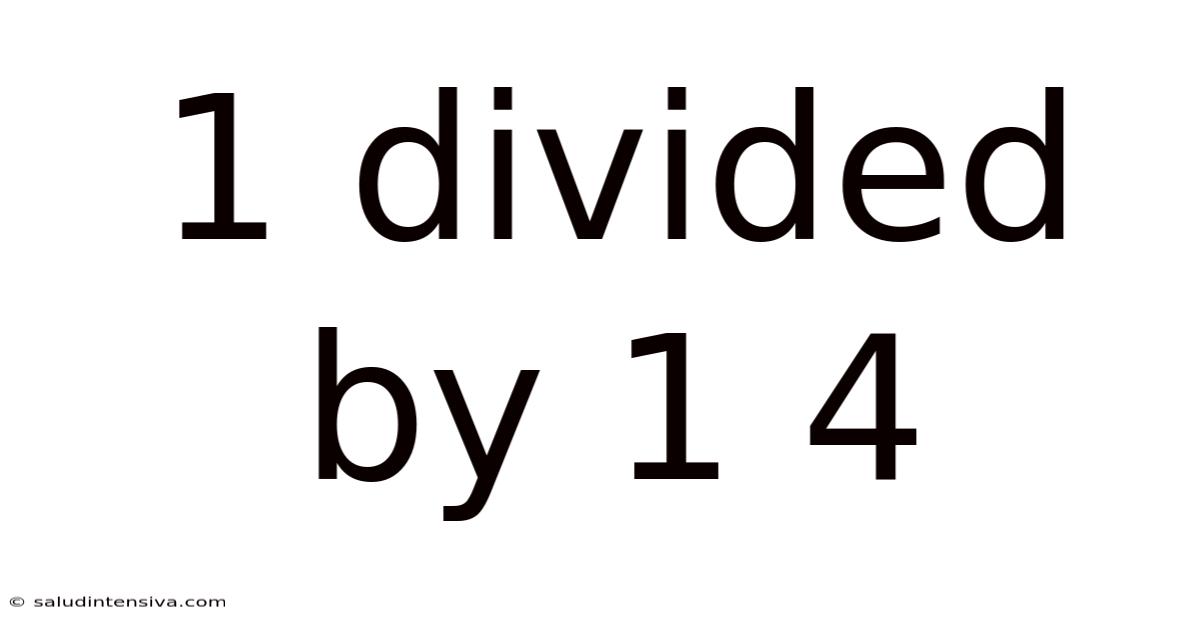
Table of Contents
Understanding 1 Divided by 1 ¼: A Deep Dive into Fraction Division
This article explores the seemingly simple yet fundamentally important concept of dividing 1 by 1 ¼ (one and one-quarter). We'll break down the process step-by-step, offering multiple approaches to solve this problem and delving into the underlying mathematical principles. Understanding this concept is crucial for mastering fraction division and building a strong foundation in arithmetic.
Introduction: Why is this Important?
The division of 1 by 1 ¼, or 1 ÷ 1 ¼, might seem trivial at first glance. However, it serves as an excellent example to solidify your understanding of fraction division. Mastering this seemingly simple calculation unlocks the ability to tackle more complex problems involving fractions, decimals, and even algebraic equations. This understanding is critical for various applications, from everyday calculations like recipe adjustments to more advanced mathematical and scientific endeavors. This article will guide you through the different methods to solve this problem and explain the reasoning behind each step.
Method 1: Converting to Improper Fractions
The most straightforward method to divide fractions involves converting mixed numbers (like 1 ¼) into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert the mixed number to an improper fraction: 1 ¼ can be rewritten as (1 x 4) + 1 / 4 = 5/4.
-
Rewrite the division problem: Our problem becomes 1 ÷ 5/4.
-
Invert and multiply: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 5/4 is 4/5. Therefore, the problem becomes 1 x 4/5.
-
Solve the multiplication: Multiplying 1 by any fraction results in that fraction itself. Therefore, the answer is 4/5.
-
Convert to decimal (optional): To express the answer as a decimal, divide the numerator (4) by the denominator (5): 4 ÷ 5 = 0.8.
Therefore, 1 ÷ 1 ¼ = 4/5 = 0.8
Method 2: Using Decimal Representation
This method utilizes the decimal equivalents of the numbers involved.
-
Convert the mixed number to a decimal: 1 ¼ is equivalent to 1.25.
-
Perform the division: Divide 1 by 1.25: 1 ÷ 1.25 = 0.8
This method provides a quick and easy solution, particularly if you're comfortable working with decimals.
Method 3: Long Division with Fractions
This method demonstrates the process of long division using fractions directly. While it might seem more complex initially, it provides a deeper understanding of the underlying process.
-
Set up the long division: We're dividing 1 by 1 ¼. We can represent 1 as 4/4. So, the problem is 4/4 ÷ 5/4.
-
Remember the rule for dividing fractions: We keep the first fraction (dividend) the same, change the division sign to multiplication, and invert the second fraction (divisor). This gives us (4/4) x (4/5).
-
Multiply the numerators and denominators: (4 x 4) / (4 x 5) = 16/20
-
Simplify the fraction: Both the numerator and denominator are divisible by 4. Simplifying gives us 4/5.
This method confirms our previous results, highlighting the consistency of different approaches.
The Mathematical Principles Behind Fraction Division
At the heart of fraction division lies the concept of finding how many times one fraction fits into another. When we divide 1 by 1 ¼, we are essentially asking, "How many 1 ¼ units fit into 1 unit?"
The key idea is reciprocals. The reciprocal of a fraction is obtained by swapping its numerator and denominator. The reason we invert and multiply is because multiplication is the inverse operation of division. Multiplying by the reciprocal effectively "undoes" the division, leading us to the correct answer.
This concept extends to all fraction division problems. The algorithm of "invert and multiply" is a shortcut to a more complex mathematical process involving finding a common denominator and then dividing the numerators.
Practical Applications: Real-World Examples
Understanding fraction division has numerous practical applications. Here are a few examples:
-
Recipe Scaling: If a recipe calls for 1 ¼ cups of flour and you want to halve the recipe, you would divide 1 ¼ by 2 (or multiply by ½), giving you ⅝ cup of flour.
-
Measurement Conversions: Converting between different units of measurement often involves fraction division. For instance, converting inches to feet requires dividing by 12 (since there are 12 inches in a foot).
-
Sharing Resources: If you have 1 pizza and need to divide it equally among 1 ¼ people (a strange scenario, but illustrative!), you'd perform 1 ÷ 1 ¼ to find out what portion each person receives.
-
Financial Calculations: Many financial calculations involve proportions and fractions, where division plays a significant role.
-
Engineering and Physics: Proportionality and ratios are fundamental in numerous engineering and physics applications, with fraction division being integral to many calculations.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Yes, most calculators can handle fraction division. Simply input the problem as 1 ÷ 1.25 or use the fraction function if your calculator has one.
Q: Why is the answer less than 1?
A: Because we're dividing 1 by a number greater than 1 (1 ¼). When we divide a number by a larger number, the result is always less than 1.
Q: What if the dividend (the number being divided) was larger than the divisor?
A: If the dividend was larger than the divisor, the result would be greater than 1. For example, 2 ÷ 1 ¼ would result in a number larger than 1.
Q: Are there other ways to solve this problem?
A: While the methods outlined above are the most common and efficient, there are other mathematical approaches that could be used, involving more complex manipulations of fractions or employing different properties of numbers. However, these methods are often more convoluted than the simpler methods described.
Conclusion: Mastering Fraction Division
Dividing 1 by 1 ¼, while seemingly a simple problem, provides a powerful illustration of fundamental mathematical concepts. Understanding the methods outlined in this article—converting to improper fractions, using decimal representation, and performing long division with fractions—strengthens your grasp of fraction division. This understanding is not only crucial for academic success but also highly valuable in various practical applications throughout life. By mastering fraction division, you're building a strong foundation for tackling more complex mathematical challenges and enhancing your problem-solving skills. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the easier and more intuitive these concepts will become.
Latest Posts
Latest Posts
-
How Long Is 195 Minutes
Sep 19, 2025
-
12 16 In Lowest Terms
Sep 19, 2025
-
18 25 As A Percentage
Sep 19, 2025
-
Home Depreciation Calculator For Taxes
Sep 19, 2025
-
How To Calculate Pixel Size
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.