1 Million Divided By 50
saludintensiva
Sep 24, 2025 · 6 min read
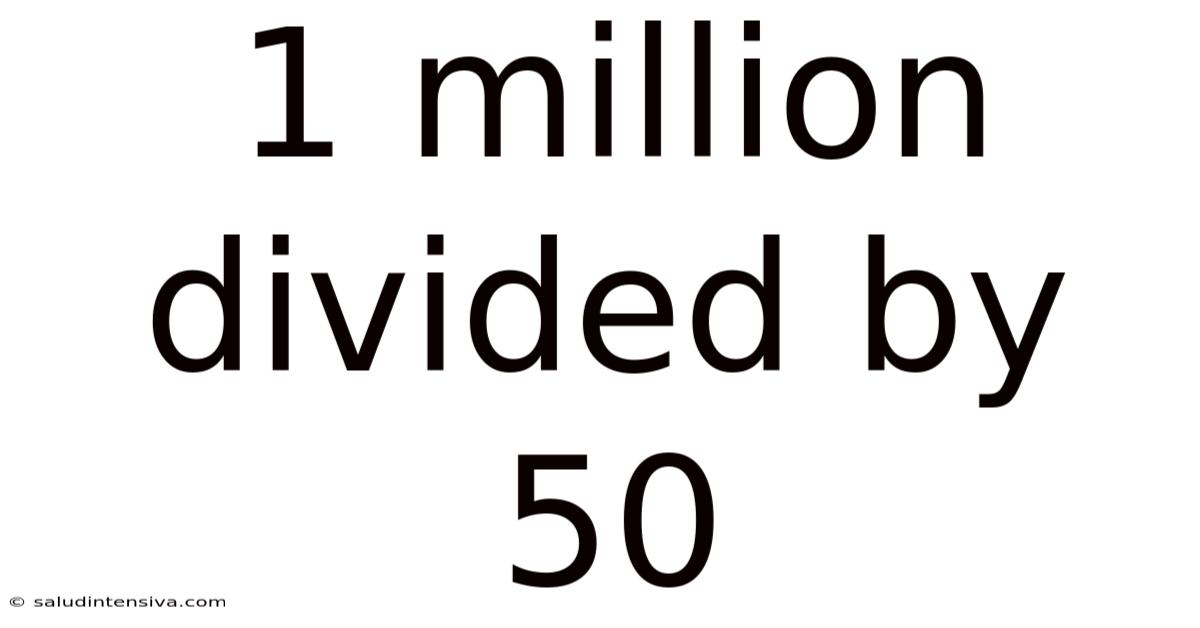
Table of Contents
One Million Divided by Fifty: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of one million divided by fifty (1,000,000 ÷ 50), delving far beyond the immediate answer. We'll uncover the underlying mathematical principles, explore various methods of solving this problem, and examine real-world applications where such calculations are crucial. Understanding this seemingly basic division problem lays the foundation for grasping more complex mathematical concepts and their practical uses. We'll cover everything from basic arithmetic to more advanced techniques, making this a comprehensive guide for learners of all levels.
Understanding the Problem: 1,000,000 ÷ 50
At its core, the problem 1,000,000 ÷ 50 asks: "How many times does 50 fit into 1,000,000?" This is a fundamental division problem, representing the inverse operation of multiplication. If we multiply 50 by a certain number to get 1,000,000, then dividing 1,000,000 by 50 will give us that same number.
Method 1: Long Division
The traditional method of solving this is through long division. While it might seem cumbersome for this specific problem, understanding long division is vital for tackling more complex division problems. Here’s how it works:
-
Set up the problem: Write 1,000,000 as the dividend (the number being divided) and 50 as the divisor (the number doing the dividing).
-
Divide: Start by asking how many times 50 goes into 1 (it doesn't). Then, consider how many times 50 goes into 10 (it doesn't either). Continue this process until you reach 100. 50 goes into 100 two times (50 x 2 = 100). Write '2' above the '00' in 1,000,000.
-
Multiply and subtract: Multiply the quotient (2) by the divisor (50), resulting in 100. Subtract this from the first three digits of the dividend (100 - 100 = 0).
-
Bring down: Bring down the next three digits (000).
-
Repeat: Now ask how many times 50 goes into 000. It goes zero times. Write '0' above the next three digits.
-
Bring down and repeat: Bring down the remaining three digits (000). Again, 50 goes into 000 zero times. Write another '0'.
-
Final Answer: The final result is 20,000. Therefore, 1,000,000 ÷ 50 = 20,000.
Method 2: Simplification and Multiplication
A simpler approach involves simplifying the problem before performing the division. We can rewrite 50 as 5 x 10. This allows us to break down the division into smaller, more manageable steps:
-
Divide by 10: Dividing 1,000,000 by 10 is straightforward; simply remove one zero: 100,000.
-
Divide by 5: Now we need to divide 100,000 by 5. This can be done using long division or by recognizing that 100,000 is 20,000 fives (100,000 / 5 = 20,000).
-
Final Answer: The result remains 20,000. This method demonstrates that breaking down complex problems into simpler steps can often lead to a more efficient solution.
Method 3: Using Fractions
We can represent the division problem as a fraction: 1,000,000/50. Simplifying this fraction is another effective method:
- Simplify the fraction: Both the numerator (1,000,000) and the denominator (50) are divisible by 50. Dividing both by 50 gives us 20,000/1, which simplifies to 20,000.
Method 4: Calculator
For quick calculations, a calculator is the most efficient tool. Simply input 1,000,000 ÷ 50 and the calculator will instantly provide the answer: 20,000. While convenient, understanding the underlying mathematical principles remains crucial for problem-solving beyond simple calculations.
Real-World Applications
The concept of dividing a large number by a smaller number, as exemplified by 1,000,000 ÷ 50, has numerous practical applications across various fields:
-
Finance: Calculating per-share earnings, determining the average cost of an investment, or distributing profits among partners often involve dividing large sums of money.
-
Engineering: Dividing total project costs by the number of days allocated helps in budgeting and project management.
-
Data Analysis: Averaging large datasets, such as calculating the average income of a population or the average temperature over a year, requires dividing the sum of values by the number of data points.
-
Business: Dividing total sales by the number of units sold helps to calculate the average selling price of a product. Similarly, dividing total expenses by the number of employees helps determine the average expense per employee.
-
Science: Calculating the average speed, density, or concentration often involves division. For example, dividing the total distance traveled by the time taken provides the average speed.
-
Everyday Life: Sharing a large amount of money or items evenly among a group of people involves division. For example, dividing a large pizza among friends or distributing candies evenly among children.
Mathematical Principles Involved
This seemingly simple calculation touches upon several important mathematical principles:
-
Division: The fundamental arithmetic operation of splitting a quantity into equal parts.
-
Factors and Multiples: Understanding that 50 is a factor of 1,000,000 and 1,000,000 is a multiple of 50 is crucial for simplification.
-
Fractions: Representing the division problem as a fraction allows for simplification and a deeper understanding of the relationship between the numerator and denominator.
-
Decimal System: The base-10 number system, which utilizes powers of 10, simplifies calculations involving large numbers.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers were different? How would I approach a similar problem with different values?
- A: The same principles apply. Regardless of the specific numbers, you can use long division, simplification, fractions, or a calculator to solve the problem. The key is to understand the underlying concept of division.
-
Q: Why is it important to understand different methods of division?
- A: Understanding multiple methods provides flexibility and allows you to choose the most efficient approach depending on the complexity of the problem and the available tools.
-
Q: Can I use a calculator for all division problems?
- A: While calculators are convenient, understanding the underlying mathematical principles remains important for problem-solving, especially in more complex scenarios. Calculators can be a tool, but not a replacement for comprehension.
-
Q: What are some common mistakes to avoid when performing division?
- A: Common mistakes include incorrect placement of the decimal point, errors in subtraction, and misinterpreting the remainder. Careful attention to detail is key.
Conclusion
The seemingly simple calculation of 1,000,000 ÷ 50, yielding the answer 20,000, opens a door to a deeper understanding of division and its wide-ranging applications. From the basic principles of long division to more sophisticated methods like fraction simplification, mastering this calculation empowers you with practical skills applicable in diverse fields. Whether you're dealing with financial transactions, analyzing data, or tackling everyday challenges, a solid grasp of division is an invaluable asset. This article has explored multiple approaches to solving this problem, highlighting the importance of understanding the underlying mathematical concepts and the diverse contexts in which this type of calculation is essential. Remember, the journey to mastering mathematics is a process of understanding, practice, and application – and this seemingly simple calculation is a perfect starting point.
Latest Posts
Latest Posts
-
What Is Half Of 100
Sep 24, 2025
-
People Born In May 11
Sep 24, 2025
-
Make Money On Feet Finder
Sep 24, 2025
-
Convert 25 Cm To Inches
Sep 24, 2025
-
How Long Is 1 8 Hours
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 Million Divided By 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.