10 - 2 X 3
saludintensiva
Sep 18, 2025 · 5 min read
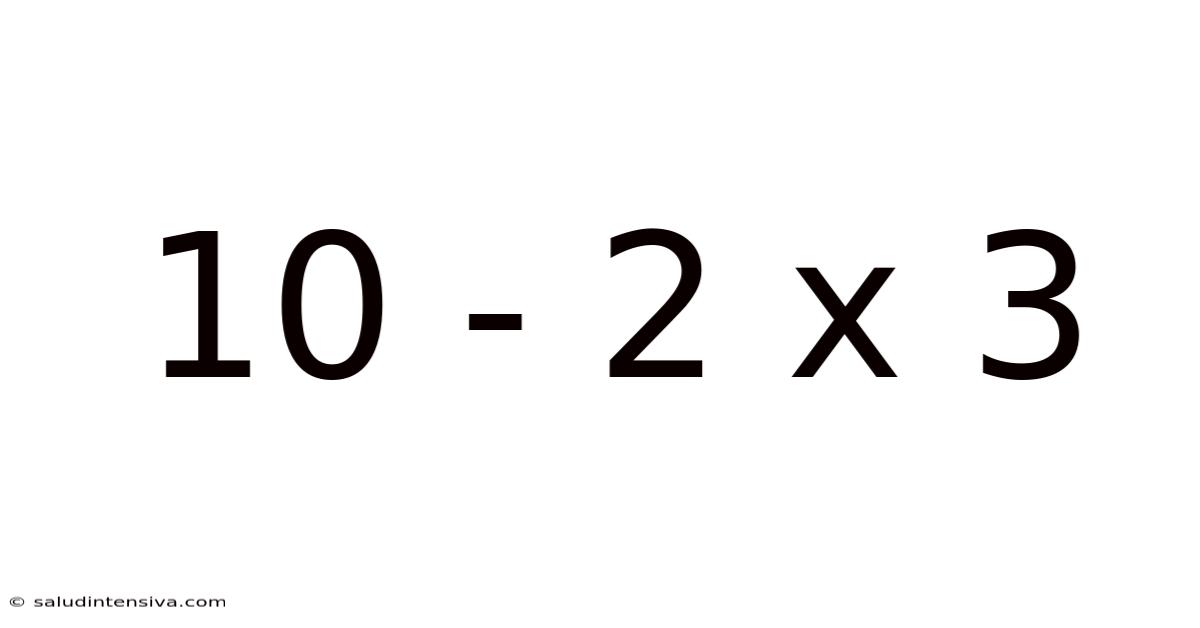
Table of Contents
Unraveling the Mystery: A Deep Dive into 10 - 2 x 3
This article delves into the seemingly simple mathematical expression "10 - 2 x 3," exploring its solution, the underlying principles, and the common pitfalls that can lead to incorrect answers. We will unpack the order of operations, also known as PEMDAS/BODMAS, and demonstrate why understanding this fundamental concept is crucial in mathematics. This seemingly basic equation serves as a gateway to understanding more complex algebraic manipulations and problem-solving strategies. We'll also look at real-world applications and answer frequently asked questions, ensuring a comprehensive understanding for learners of all levels.
Understanding the Order of Operations (PEMDAS/BODMAS)
The key to correctly solving "10 - 2 x 3" lies in understanding the order of operations. This set of rules dictates the sequence in which mathematical operations should be performed to ensure a consistent and unambiguous result. Two common acronyms represent this order:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- BODMAS: Brackets, Orders, Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Both acronyms represent the same order of operations; they simply use different terminology for the same concepts. "Parentheses" and "Brackets" refer to the same thing – expressions enclosed in ( ). "Exponents" and "Orders" both refer to powers and roots. The crucial point is that multiplication and division have equal precedence, as do addition and subtraction. When faced with these operations in the same expression, we work from left to right.
Solving 10 - 2 x 3 Step-by-Step
Now, let's apply PEMDAS/BODMAS to solve "10 - 2 x 3":
-
Multiplication First: According to PEMDAS/BODMAS, multiplication comes before subtraction. Therefore, we perform the multiplication operation first: 2 x 3 = 6.
-
Subtraction Next: Our expression now simplifies to: 10 - 6.
-
Final Result: Performing the subtraction, we get the final answer: 10 - 6 = 4.
Therefore, the correct solution to 10 - 2 x 3 is 4.
Common Mistakes and Misconceptions
A common error when solving this type of equation is performing the operations from left to right without considering the order of operations. This leads to an incorrect answer:
- Incorrect Calculation (Left to Right): 10 - 2 = 8; 8 x 3 = 24. This approach yields an incorrect answer of 24.
This highlights the importance of adhering strictly to the order of operations. Ignoring PEMDAS/BODMAS can lead to significant errors, especially in more complex calculations.
The Importance of Parentheses/Brackets
Parentheses or brackets are used to group operations and override the standard order of operations. They force the enclosed operations to be performed before any operations outside the parentheses. Let's consider some examples:
-
(10 - 2) x 3: In this case, the parentheses dictate that the subtraction (10 - 2) is performed first: 8 x 3 = 24. The answer is drastically different because of the parentheses.
-
10 - (2 x 3): Here, the parentheses indicate that the multiplication (2 x 3) is performed first: 10 - 6 = 4, resulting in the same answer as the original problem.
These examples demonstrate how parentheses can significantly alter the outcome of a calculation. Using parentheses correctly is essential for accurately representing mathematical expressions and avoiding ambiguity.
Real-World Applications
Understanding the order of operations is not just an academic exercise; it's essential for numerous real-world applications, including:
-
Financial Calculations: Calculating compound interest, discounts, taxes, and other financial transactions requires a clear understanding of the order of operations. Incorrect calculations can lead to significant financial errors.
-
Programming and Coding: Programming languages follow the order of operations implicitly. Understanding this principle is vital for writing accurate and efficient code.
-
Engineering and Physics: Many engineering and physics formulas involve multiple operations. Correctly applying the order of operations ensures accurate results in calculations related to forces, motion, energy, and other physical phenomena.
-
Everyday Calculations: Even simple everyday tasks, like calculating the total cost of groceries or determining the remaining balance after making payments, require a basic understanding of order of operations.
Expanding on the Concept: Beyond Simple Arithmetic
The principle of the order of operations extends far beyond simple arithmetic expressions like "10 - 2 x 3." It forms the foundation for more advanced mathematical concepts, including:
-
Algebra: Solving algebraic equations often involves multiple operations and requires a strong understanding of the order of operations to correctly manipulate expressions.
-
Calculus: Differential and integral calculus extensively utilize operations such as addition, subtraction, multiplication, division, exponentiation, and roots, all of which necessitate a firm grasp of the order of operations.
-
Linear Algebra: Linear algebra involves manipulating matrices and vectors, which frequently involves a series of operations that must be performed in the correct order to achieve accurate results.
Frequently Asked Questions (FAQ)
Q: Why is the order of operations important?
A: The order of operations ensures that everyone gets the same answer when solving a mathematical expression. Without it, there would be ambiguity and multiple possible solutions for the same expression.
Q: What if there are multiple multiplication and division operations in an equation?
A: Perform these operations from left to right.
Q: What if there are multiple addition and subtraction operations in an equation?
A: Perform these operations from left to right.
Q: Can I use a calculator to solve this?
A: Yes, most scientific calculators automatically follow the order of operations. However, it's still crucial to understand the underlying principles to avoid misinterpreting results or using a calculator incorrectly.
Q: Is there a difference between PEMDAS and BODMAS?
A: No, they represent the same order of operations, just using slightly different terminology.
Conclusion: Mastering the Fundamentals
The seemingly simple equation "10 - 2 x 3" serves as a powerful illustration of the importance of the order of operations. Understanding PEMDAS/BODMAS is fundamental to achieving accurate results in mathematics and its numerous applications across various fields. By mastering this concept, you'll build a strong foundation for tackling more complex mathematical challenges and problem-solving tasks. Remember that consistent practice and a keen understanding of the underlying principles are key to mastering this essential mathematical skill. Don't just memorize the acronym; understand why the order matters and how it impacts the outcome of your calculations. This will not only improve your mathematical skills but also enhance your critical thinking and problem-solving abilities.
Latest Posts
Latest Posts
-
2 To The 6 Power
Sep 18, 2025
-
Write 1 4 As A Percent
Sep 18, 2025
-
20 4 In Decimal Form
Sep 18, 2025
-
19 4 As A Decimal
Sep 18, 2025
-
4 To The 3rd Power
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 10 - 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.