10 4 In Simplest Form
saludintensiva
Sep 11, 2025 · 6 min read
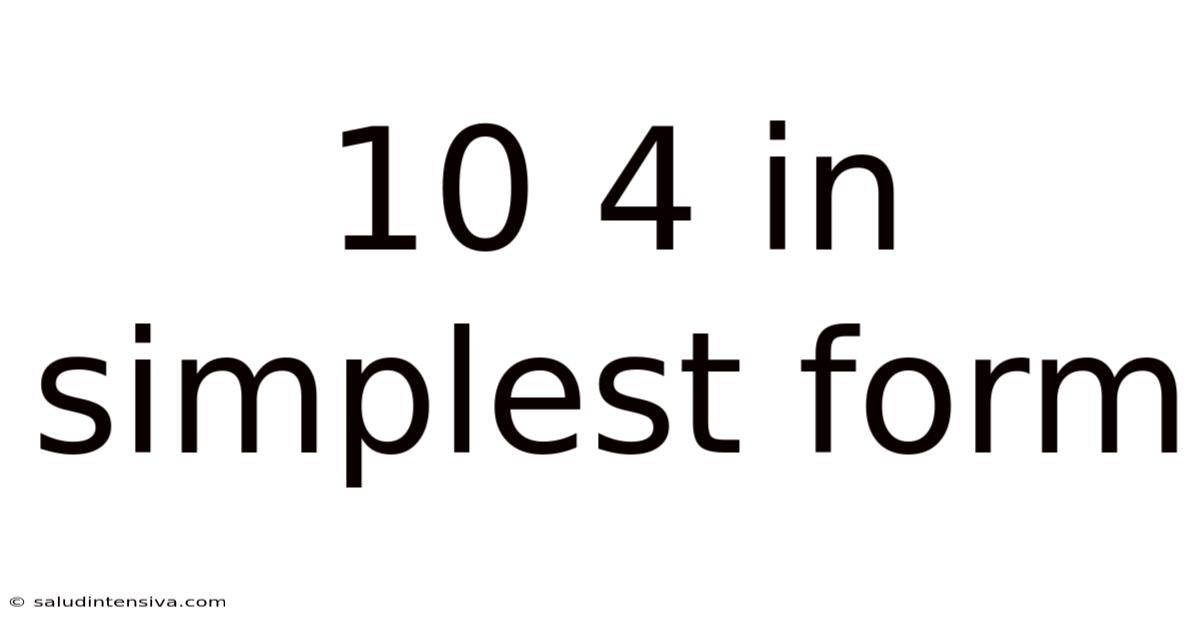
Table of Contents
Simplifying Fractions: A Deep Dive into 10/4
Understanding fractions is a fundamental skill in mathematics, forming the bedrock for more advanced concepts. This article will provide a comprehensive guide to simplifying fractions, using the example of 10/4 as our central case study. We will delve into the process step-by-step, explore the underlying mathematical principles, and address frequently asked questions, ensuring a complete understanding for learners of all levels. By the end, you'll not only know the simplest form of 10/4 but also possess the tools to simplify any fraction with confidence.
What is a Fraction?
Before diving into simplification, let's establish a clear understanding of what a fraction represents. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 10/4, 10 is the numerator and 4 is the denominator. This means we have 10 parts out of a total of 4 equal parts. This might seem counterintuitive at first – how can you have 10 parts of something divided into only 4? We'll see how this resolves itself through simplification.
Simplifying Fractions: The Concept of Greatest Common Factor (GCF)
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This involves finding the greatest common factor (GCF) of the numerator and the denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder.
To simplify 10/4, we need to find the GCF of 10 and 4. Let's explore a few methods to do this:
1. Listing Factors:
- Factors of 10: 1, 2, 5, 10
- Factors of 4: 1, 2, 4
The largest number that appears in both lists is 2. Therefore, the GCF of 10 and 4 is 2.
2. Prime Factorization:
This method is particularly useful for larger numbers. We break down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 10: 2 x 5
- Prime factorization of 4: 2 x 2
The common prime factor is 2. Therefore, the GCF is 2.
Simplifying 10/4: A Step-by-Step Guide
Now that we know the GCF of 10 and 4 is 2, we can simplify the fraction:
-
Divide both the numerator and the denominator by the GCF:
10 ÷ 2 = 5 4 ÷ 2 = 2
-
The simplified fraction is: 5/2
Therefore, the simplest form of 10/4 is 5/2. This is also known as an improper fraction because the numerator is larger than the denominator.
Converting Improper Fractions to Mixed Numbers
Improper fractions often represent a whole number and a fraction. We can convert 5/2 into a mixed number which is a combination of a whole number and a proper fraction (numerator smaller than the denominator).
-
Divide the numerator by the denominator: 5 ÷ 2 = 2 with a remainder of 1
-
The whole number is the quotient: 2
-
The numerator of the fraction is the remainder: 1
-
The denominator remains the same: 2
Therefore, 5/2 is equivalent to 2 1/2. This means that 10/4 represents two and a half whole units.
Visual Representation of 10/4
Imagine you have a pizza cut into 4 equal slices. The fraction 10/4 means you have 10 of these slices. Since each pizza has only 4 slices, you have more than one whole pizza. You can form two complete pizzas (8 slices) and have 2 slices left over from a third pizza. This visually demonstrates why 10/4 simplifies to 2 1/2.
Mathematical Explanation: Equivalence of Fractions
Simplifying a fraction doesn't change its value; it simply expresses it in a more concise and manageable form. When we divide both the numerator and the denominator by the GCF, we are essentially multiplying the fraction by 1 (in the form of GCF/GCF), which doesn't alter its value. For example:
(10/4) x (2/2) = 20/8 (This is an equivalent fraction)
However, 20/8 is still not in its simplest form. Continuing the simplification process, dividing both by 4 (the GCF of 20 and 8):
20/8 = 5/2
This demonstrates that all simplified forms of a fraction are equivalent.
Different Methods for Finding the GCF
Besides listing factors and prime factorization, other methods can help determine the GCF, especially for larger numbers:
- Euclidean Algorithm: This iterative method repeatedly applies the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
- Using a calculator: Many calculators have a GCF function, simplifying the process significantly.
Choosing the most efficient method depends on the numbers involved and your familiarity with different techniques.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to work with in calculations and comparisons. It presents the fraction in its most efficient and understandable form.
Q2: What happens if I divide the numerator and denominator by a common factor that is not the GCF?
A2: You will get an equivalent fraction, but it will not be in its simplest form. You would need to further simplify the resulting fraction by dividing by any remaining common factors.
Q3: Can I simplify a fraction if the numerator and denominator have no common factors other than 1?
A3: No. If the GCF is 1, the fraction is already in its simplest form.
Q4: Can a fraction be simplified if one of the numbers is a prime number?
A4: Yes, if the other number is a multiple of that prime number. For example, 6/2 simplifies to 3/1 (or simply 3) because 2 is a factor of 6.
Q5: Is there a way to simplify fractions with decimals?
A5: To simplify fractions containing decimals, you first need to convert the decimals into fractions, then find the greatest common factor and simplify accordingly.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a crucial skill in mathematics. By understanding the concept of the greatest common factor and applying the appropriate methods, you can confidently reduce any fraction to its simplest form. We've explored the process using 10/4 as an example, illustrating the steps involved, providing alternative methods for finding the GCF, and addressing common questions. Remember, practice is key. The more you work with fractions, the more intuitive and efficient the simplification process will become. Mastering fraction simplification opens doors to a deeper understanding of numerous mathematical concepts and applications.
Latest Posts
Latest Posts
-
Convert 500 M To Feet
Sep 11, 2025
-
Variance Of Probability Distribution Calculator
Sep 11, 2025
-
Negative Numbers In Scientific Notation
Sep 11, 2025
-
What Is 3 1 Ratio
Sep 11, 2025
-
Square Roots And Pythagorean Theorem
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10 4 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.