10 6 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
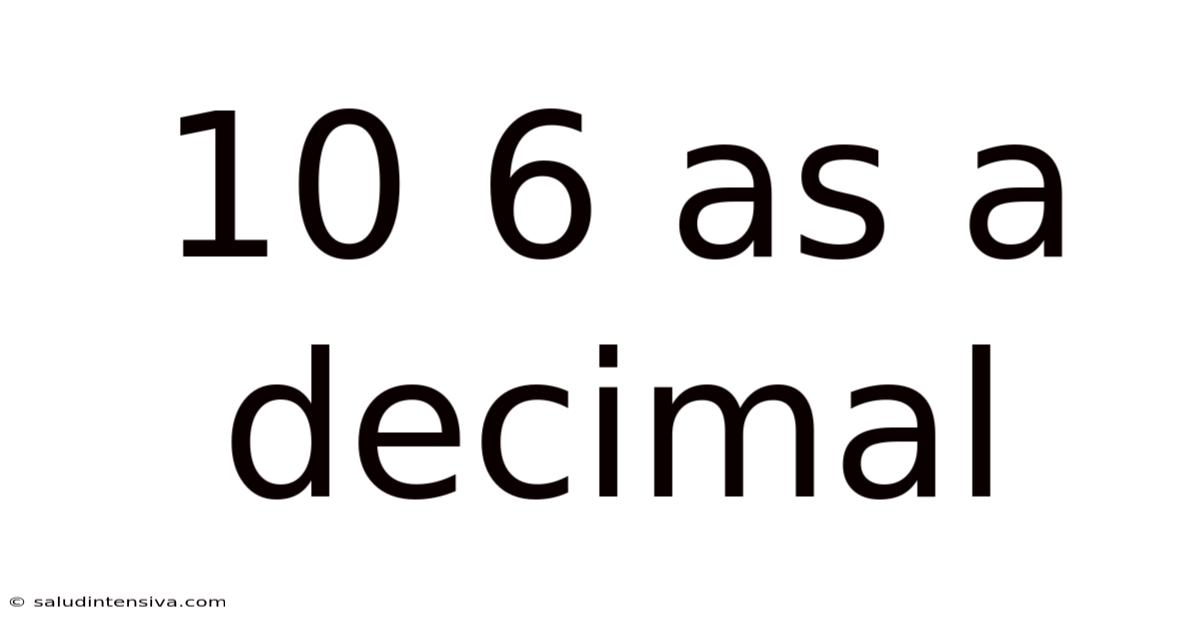
Table of Contents
Decoding 10/6 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics. This article delves deep into converting the fraction 10/6 into its decimal form, exploring various methods, providing detailed explanations, and addressing common questions. We'll go beyond a simple answer, ensuring you grasp the underlying concepts and can confidently tackle similar conversions in the future. This comprehensive guide will cover the core mathematical principles involved, practical applications, and troubleshooting common mistakes.
Introduction: Understanding Fractions and Decimals
Before we jump into converting 10/6, let's briefly refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). The decimal point separates the whole number part from the fractional part. Converting between fractions and decimals is a crucial skill in various mathematical applications.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. In this case, we divide the numerator (10) by the denominator (6):
10 ÷ 6 = 1.66666...
The result is a repeating decimal, indicated by the ellipsis (...). The digit 6 repeats infinitely. This is often represented as 1.6̅ or 1.6 with a bar over the 6. This signifies that the 6 continues indefinitely.
This method is simple and readily applicable using a calculator or performing long division manually. Long division provides a deeper understanding of the process, but for practical purposes, a calculator often suffices.
Method 2: Simplifying the Fraction First
Often, simplifying a fraction before converting to a decimal can make the division easier. We can simplify 10/6 by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 10 and 6 is 2. Dividing both the numerator and denominator by 2, we get:
10 ÷ 2 / 6 ÷ 2 = 5/3
Now, we can divide 5 by 3:
5 ÷ 3 = 1.66666...
This yields the same repeating decimal as before, 1.6̅. Simplifying the fraction beforehand doesn't change the decimal equivalent but can simplify the division process, especially when dealing with larger numbers.
Method 3: Converting to a Mixed Number
Another approach involves converting the improper fraction 10/6 into a mixed number. An improper fraction has a numerator larger than or equal to the denominator. To convert 10/6 to a mixed number, we divide the numerator by the denominator:
10 ÷ 6 = 1 with a remainder of 4
This means 10/6 can be written as 1 and 4/6. Simplifying 4/6 to its lowest terms (by dividing both by their GCD, which is 2), we get 2/3. Therefore, 10/6 = 1 2/3.
Now, we convert the fractional part, 2/3, to a decimal:
2 ÷ 3 = 0.66666...
Adding this to the whole number part (1), we get 1.66666..., or 1.6̅. This method breaks down the conversion into smaller, more manageable steps.
Understanding Repeating Decimals
The result, 1.6̅, is a repeating decimal. Repeating decimals occur when the division process continues indefinitely without a remainder. The repeating block of digits is called the repetend. In this case, the repetend is 6. Understanding repeating decimals is important because they represent rational numbers – numbers that can be expressed as a fraction.
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in various fields:
- Finance: Calculating interest rates, discounts, and profit margins often involve working with fractions and decimals.
- Engineering: Precision measurements and calculations in blueprints and designs require converting between fractions and decimals.
- Science: Scientific measurements and data analysis often involve fractions and decimals.
- Everyday Life: Dividing items, calculating proportions for recipes, or understanding sales discounts all utilize this skill.
Common Mistakes to Avoid
- Incorrect division: Double-check your division to ensure accuracy. A simple calculation error can lead to an incorrect decimal.
- Forgetting the repeating decimal: Remember to indicate the repeating nature of the decimal if applicable, using the bar notation (e.g., 1.6̅).
- Not simplifying fractions: Simplifying fractions before division can often make the process easier and reduce the risk of errors.
Frequently Asked Questions (FAQs)
-
Q: Can all fractions be converted to terminating decimals?
- A: No. Only fractions whose denominators, in their simplest form, have only 2 and/or 5 as prime factors will convert to terminating decimals. Other fractions will result in repeating decimals.
-
Q: What is the difference between a terminating and a repeating decimal?
- A: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.25). A repeating decimal has a digit or a sequence of digits that repeat infinitely (e.g., 0.333...).
-
Q: How can I convert a repeating decimal back into a fraction?
- A: There are specific methods to convert repeating decimals back into fractions, involving algebraic manipulation. This is a more advanced topic but involves assigning a variable to the repeating decimal and solving for its fractional equivalent.
-
Q: Are there other ways to convert 10/6 to a decimal besides division?
- A: While direct division is the most common method, the approaches outlined above (simplifying the fraction and converting to a mixed number) are alternative ways to achieve the same result. These methods can be helpful in certain contexts and improve understanding of the underlying mathematical principles.
Conclusion: Mastering Decimal Conversions
Converting fractions like 10/6 to their decimal equivalents is a fundamental mathematical skill. We've explored three distinct methods, highlighted the significance of repeating decimals, and addressed common pitfalls. By understanding these techniques and practicing regularly, you'll build a strong foundation in fraction-to-decimal conversion, a skill applicable across numerous disciplines and everyday scenarios. Remember that while calculators are helpful tools, understanding the underlying mathematical principles is key to mastering this important skill. Practice converting various fractions to decimals to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Lcm Of 24 And 28
Sep 10, 2025
-
Greatest Common Factor For 21
Sep 10, 2025
-
Gcf Of 18 And 40
Sep 10, 2025
-
Gcf Of 6 And 24
Sep 10, 2025
-
400 Troy Oz To Lbs
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 10 6 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.