10/6 As A Mixed Number
saludintensiva
Sep 15, 2025 · 4 min read
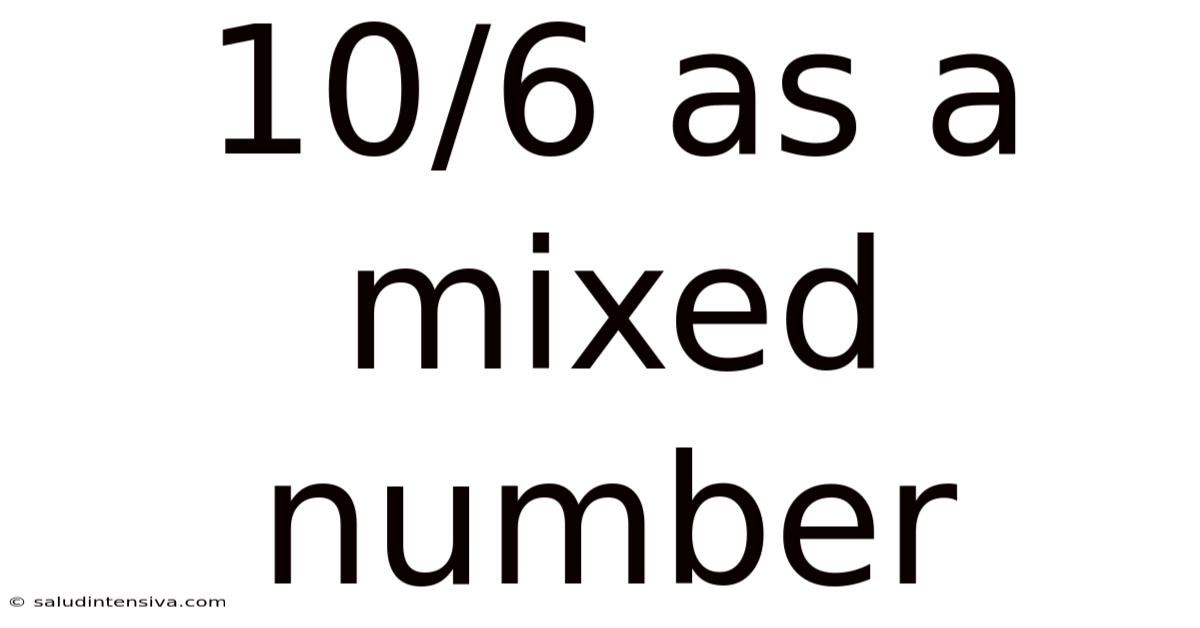
Table of Contents
Understanding 10/6 as a Mixed Number: A Comprehensive Guide
Fractions are fundamental building blocks in mathematics, forming the basis for more advanced concepts. Understanding how to represent fractions in different forms, like mixed numbers, is crucial for problem-solving and deeper mathematical comprehension. This comprehensive guide will delve into the meaning of 10/6, explaining how to convert it into a mixed number, providing the underlying mathematical principles, and addressing frequently asked questions. We'll explore practical applications and offer tips to solidify your understanding of this important concept.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). For example, 1 ¾ is a mixed number; it represents one whole unit and three-quarters of another. Mixed numbers offer a more intuitive way to represent fractions larger than one.
Converting 10/6 to a Mixed Number: Step-by-Step
The fraction 10/6 represents ten sixths. Since the numerator (10) is larger than the denominator (6), it's an improper fraction. To convert it to a mixed number, we need to determine how many whole units are contained within 10/6 and what fraction remains.
Here's a step-by-step guide:
-
Divide the numerator by the denominator: Divide 10 by 6. This gives us 1 with a remainder of 4.
-
Identify the whole number: The quotient (result of the division) becomes the whole number part of the mixed number. In this case, the whole number is 1.
-
Determine the remaining fraction: The remainder (4) becomes the numerator of the fraction, while the original denominator (6) remains unchanged. This gives us the fraction 4/6.
-
Combine the whole number and fraction: Combine the whole number from step 2 and the fraction from step 3 to form the mixed number. Therefore, 10/6 as a mixed number is 1 ⁴⁄₆.
Simplifying the Mixed Number
The mixed number 1 ⁴⁄₆ can be further simplified. Both the numerator (4) and denominator (6) are divisible by 2. Dividing both by 2, we get the simplified fraction ²⁄₃.
Therefore, the fully simplified mixed number representation of 10/6 is 1 ²⁄₃.
Mathematical Explanation: The Division Process
The process of converting an improper fraction to a mixed number is essentially a division problem. We are dividing the numerator into equal parts determined by the denominator. The quotient represents the number of whole units, and the remainder represents the fraction of a whole unit remaining.
Let's visualize this with 10/6: Imagine you have 10 pizzas, and you want to divide them equally among 6 people. Each person would receive one whole pizza (1), and you'd have 4 slices left over. Since each pizza has 6 slices, those 4 leftover slices represent ⁴⁄₆ of a pizza. Therefore, each person receives 1 ²⁄₃ pizzas.
Real-World Applications of Mixed Numbers
Mixed numbers are prevalent in everyday life. Here are a few examples:
-
Cooking and Baking: Recipes often call for measurements in mixed numbers, such as 2 ½ cups of flour or 1 ¼ teaspoons of baking powder.
-
Measurements: Measuring lengths, weights, or volumes frequently involves mixed numbers. For example, a board might be 2 ⅓ feet long.
-
Time: Time is often expressed using mixed numbers. For instance, we might say "1 hour and a half" or "2 hours and 15 minutes," which can be represented as mixed numbers.
Frequently Asked Questions (FAQ)
-
Why do we convert improper fractions to mixed numbers? Mixed numbers provide a more user-friendly and easily understandable representation of fractions greater than one. They are often preferred in real-world applications and for easier comparisons.
-
What if the remainder is zero after dividing the numerator by the denominator? If the remainder is zero, it means the improper fraction is already a whole number. For example, 12/3 = 4, which is a whole number.
-
Can I convert a mixed number back to an improper fraction? Absolutely! To do so, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, to convert 1 ²⁄₃ back to an improper fraction: (1 x 3) + 2 = 5, so the improper fraction is ⁵⁄₃.
-
Are there different ways to convert improper fractions to mixed numbers? While the method described above is the most common and straightforward, there are other methods, some involving visual aids like fraction bars or circles, that can aid understanding. The core principle of division remains the same, regardless of the approach.
Conclusion: Mastering Mixed Numbers
Understanding how to represent fractions as mixed numbers is a crucial skill in mathematics. The ability to convert between improper fractions and mixed numbers allows for greater flexibility in problem-solving and facilitates a deeper understanding of fractional concepts. By mastering this fundamental skill, you'll be better equipped to handle more complex mathematical problems in various contexts, from everyday calculations to advanced algebraic equations. Remember, practice is key! The more you work with fractions and mixed numbers, the more comfortable and proficient you'll become. The seemingly simple task of converting 10/6 to 1 ²⁄₃ lays the groundwork for a robust understanding of fractions and their applications throughout your mathematical journey. Don't hesitate to review these steps, practice with different examples, and utilize visual aids to reinforce your learning.
Latest Posts
Latest Posts
-
0 5 Repeating As A Fraction
Sep 15, 2025
-
Gcf Of 25 And 30
Sep 15, 2025
-
Lcm Of 8 4 6
Sep 15, 2025
-
4 2 3 3 4
Sep 15, 2025
-
Gcf Of 20 And 10
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 10/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.