10/8 As A Mixed Number
saludintensiva
Sep 11, 2025 · 6 min read
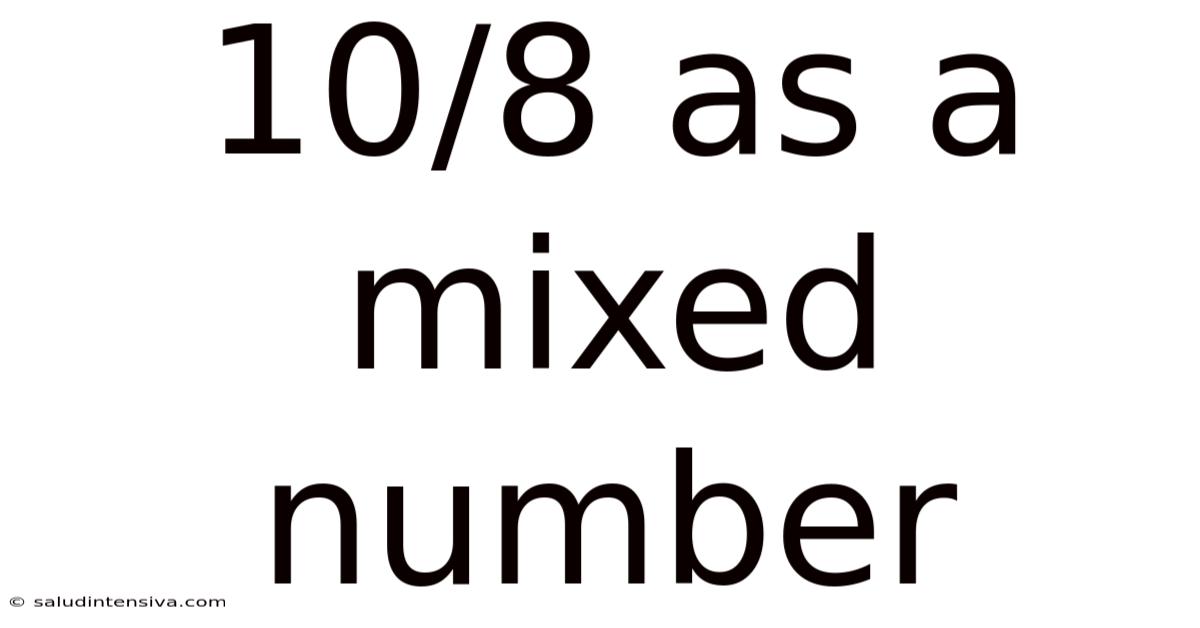
Table of Contents
Understanding 10/8 as a Mixed Number: A Comprehensive Guide
Fractions are a fundamental part of mathematics, forming the basis for many advanced concepts. Understanding how to represent fractions in different forms is crucial for problem-solving and further mathematical exploration. This article delves into the process of converting the improper fraction 10/8 into a mixed number, providing a detailed explanation suitable for learners of all levels. We'll explore the concept of mixed numbers, the steps involved in the conversion, and address common questions regarding this mathematical operation. This comprehensive guide aims to solidify your understanding of fractions and their various representations.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 2 ¾, and 5 ⅓ are all mixed numbers. They represent a quantity that is greater than one whole unit.
Conversely, an improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 5/4, 7/2, and 10/8. These fractions represent a quantity greater than or equal to one whole unit. Converting improper fractions to mixed numbers provides a more intuitive and easily understandable representation of the quantity.
Converting 10/8 to a Mixed Number: A Step-by-Step Guide
The fraction 10/8 is an improper fraction because the numerator (10) is larger than the denominator (8). To convert it into a mixed number, we follow these simple steps:
Step 1: Perform the Division
Divide the numerator (10) by the denominator (8).
10 ÷ 8 = 1 with a remainder of 2
Step 2: Identify the Whole Number and the Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
The remainder (the number left over after the division) becomes the numerator of the fractional part of the mixed number. The remainder is 2.
Step 3: Construct the Mixed Number
The denominator of the fraction in the mixed number remains the same as the denominator of the original improper fraction. Therefore, the denominator remains 8.
Combining the whole number and the fraction, we get the mixed number: 1 ²⁄₈
Therefore, 10/8 as a mixed number is 1 ²⁄₈.
Simplifying the Fraction: A Crucial Step
While 1 ²⁄₈ is a correct representation of 10/8 as a mixed number, we can simplify the fractional part further. Notice that both the numerator (2) and the denominator (8) are divisible by 2.
Dividing both by 2, we get:
2 ÷ 2 = 1 8 ÷ 2 = 4
Therefore, the simplified fractional part is ¼.
Hence, the simplified mixed number representation of 10/8 is 1 ¼. This is the preferred form as it is more concise and easier to work with in further calculations.
Visualizing the Conversion: A Practical Approach
Imagine you have 10 slices of pizza, and each pizza is cut into 8 slices. You can assemble one whole pizza using 8 slices (8/8 = 1 whole pizza). You'll have 2 slices remaining (2/8). Therefore, you have 1 whole pizza and 2/8 of another pizza, which simplifies to 1 ¼ pizzas. This visual representation helps to solidify the concept of converting improper fractions to mixed numbers.
The Importance of Understanding Mixed Numbers
Converting improper fractions to mixed numbers is not just a mathematical exercise; it has practical applications in various real-world scenarios. Consider these examples:
-
Measuring: If you are measuring ingredients for a recipe, you might need 1 ¼ cups of flour. The mixed number makes it easier to understand and measure the quantity.
-
Time: Representing time often uses mixed numbers. For instance, 1 hour and 30 minutes can be expressed as 1 ½ hours.
-
Construction: In construction and engineering, dimensions and measurements are frequently expressed using mixed numbers for precision and clarity.
-
Data analysis: Presenting data in a mixed number format can provide a clearer representation of results.
Mathematical Explanation: The Underlying Principles
The process of converting an improper fraction to a mixed number is based on the concept of division and the relationship between the numerator and the denominator. The numerator represents the total number of parts, while the denominator represents the number of parts in a whole. When the numerator is larger than the denominator, it means we have more parts than are needed to make a whole, leading to a whole number and a remaining fraction.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted into mixed numbers?
A: Yes, all improper fractions can be converted into mixed numbers. The process involves dividing the numerator by the denominator and expressing the result as a whole number and a proper fraction.
Q: What if the remainder is zero after the division?
A: If the remainder is zero, it means the improper fraction is actually a whole number. For instance, 12/4 = 3. There is no fractional part in this case.
Q: Is it always necessary to simplify the fractional part of the mixed number?
A: While not always strictly necessary, simplifying the fractional part of the mixed number is generally recommended. It makes the mixed number easier to understand and use in further calculations. Simplification ensures the fraction is in its most concise form.
Q: Can I convert a mixed number back into an improper fraction?
A: Yes, absolutely. This is the reverse process. To convert a mixed number like 1 ¼ back to an improper fraction, you multiply the whole number by the denominator and then add the numerator. The result becomes the new numerator, while the denominator remains the same. So, 1 ¼ becomes (1 x 4) + 1 = 5, giving us the improper fraction 5/4.
Q: Are there other ways to represent 10/8 besides 1 ¼?
A: While 1 ¼ is the most simplified and commonly used representation, 10/8 could also be expressed as 5/4 (after simplifying the improper fraction before converting it to a mixed number). Both 1 ¼ and 5/4 represent the same quantity.
Conclusion
Converting improper fractions to mixed numbers is a fundamental skill in mathematics. Understanding this concept is crucial for handling various mathematical operations and real-world applications. Through a step-by-step approach and clear explanations, this article aims to equip you with the knowledge and confidence to convert any improper fraction into its corresponding mixed number form with ease. Remember to always simplify your final answer for the most efficient and accurate representation. Mastering this skill lays a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Lcm Of 7 And 28
Sep 11, 2025
-
What Is 4 Of 35000
Sep 11, 2025
-
Using Density To Find Mass
Sep 11, 2025
-
What Does 3 2 Equal
Sep 11, 2025
-
Pound To Troy Ounce Conversion
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.