10 Divided By 5 6
saludintensiva
Sep 23, 2025 · 5 min read
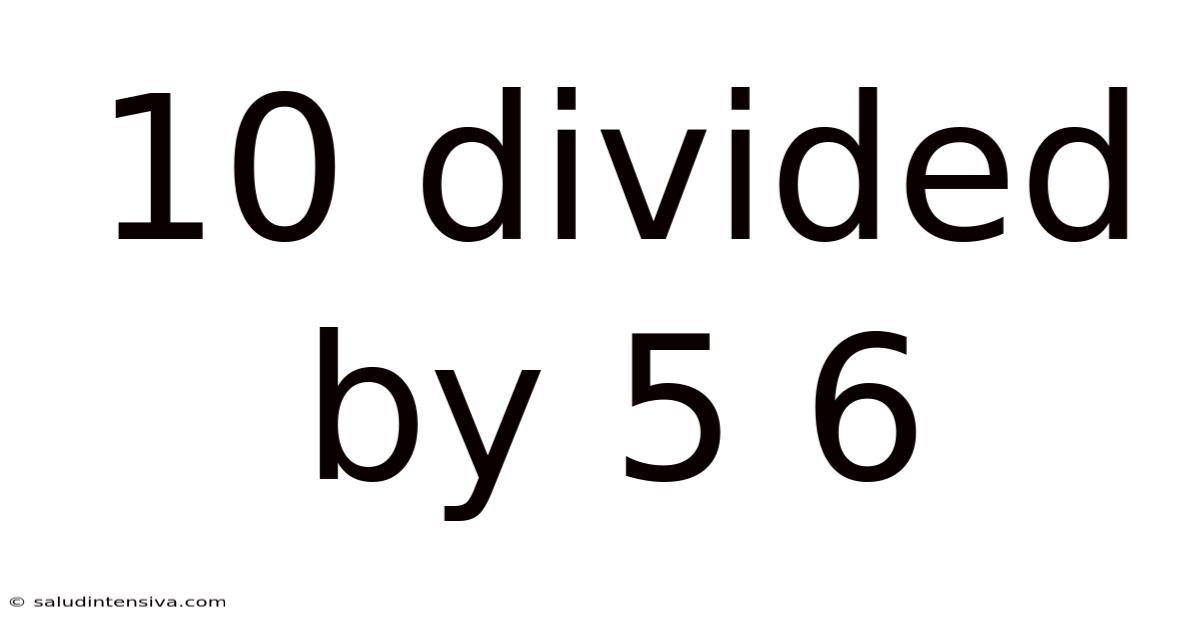
Table of Contents
Decoding 10 Divided by 5/6: A Deep Dive into Fraction Division
This article explores the seemingly simple yet conceptually rich problem of 10 divided by 5/6. We'll move beyond simply stating the answer and delve into the underlying principles of fraction division, explaining the "why" behind the calculations. This comprehensive guide will equip you with the skills to tackle similar problems with confidence, fostering a deeper understanding of mathematical operations involving fractions. We'll cover the step-by-step process, the underlying mathematical reasoning, address common misconceptions, and even explore real-world applications where this type of calculation proves useful.
Understanding Fraction Division: The Basics
Before tackling 10 divided by 5/6, let's establish a firm foundation in fraction division. The core concept revolves around the idea of finding out "how many times" one fraction fits into another. Unlike multiplying fractions, which involves straightforward multiplication of numerators and denominators, division requires a slightly different approach.
The key to understanding fraction division is the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5/6 is 6/5.
The process of dividing by a fraction is equivalent to multiplying by its reciprocal. This fundamental rule simplifies the calculation significantly.
Solving 10 Divided by 5/6: A Step-by-Step Approach
Now, let's tackle our primary problem: 10 ÷ 5/6.
Step 1: Rewrite the Whole Number as a Fraction
First, we rewrite the whole number 10 as a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 10 becomes 10/1. Our problem now looks like this:
10/1 ÷ 5/6
Step 2: Apply the Reciprocal Rule
The crucial step is to change the division operation into multiplication by using the reciprocal of the second fraction. The reciprocal of 5/6 is 6/5. Our problem transforms into:
10/1 × 6/5
Step 3: Multiply the Numerators and Denominators
Now, we simply multiply the numerators together and the denominators together:
(10 × 6) / (1 × 5) = 60/5
Step 4: Simplify the Result
Finally, we simplify the resulting fraction. 60/5 simplifies to 12.
Therefore, 10 divided by 5/6 equals 12.
The Mathematical Reasoning Behind the Reciprocal Rule
Why does changing division to multiplication by the reciprocal work? Let's explore the underlying mathematical logic.
Consider a simpler example: 2 ÷ 1/2. This asks, "How many halves are there in two wholes?" Intuitively, we know there are four halves in two wholes.
Now let's use the reciprocal method:
2 ÷ 1/2 = 2 × 2/1 = 4
The reciprocal rule works because division is fundamentally the inverse operation of multiplication. When we divide by a fraction, we're essentially asking, "What number, when multiplied by the divisor, gives the dividend?" Using the reciprocal effectively reverses the multiplication inherent in the original fraction division problem.
Addressing Common Misconceptions
Several common misconceptions surround fraction division. Let's clarify these:
- Flipping both fractions: A common mistake is flipping both fractions. Remember, only the second fraction (the divisor) is inverted.
- Incorrect simplification: Always simplify the fraction to its lowest terms after multiplying. Failing to do so leaves the answer incomplete.
- Misunderstanding the concept of reciprocals: Ensure a solid understanding of what a reciprocal is. It's not just about flipping the numbers; it's about finding the fraction that, when multiplied by the original, equals 1.
Real-World Applications
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications:
- Cooking: Scaling recipes up or down often involves dividing fractions.
- Sewing: Cutting fabric to precise measurements requires fractional calculations.
- Construction: Dividing lengths and materials accurately is crucial.
- Engineering: Calculating precise dimensions and ratios.
- Data Analysis: Working with proportions and percentages often involves fraction division.
Beyond the Basics: Extending the Concept
The principles discussed here extend to more complex problems involving mixed numbers and decimals. A mixed number is a combination of a whole number and a fraction (e.g., 2 1/2). To divide with mixed numbers, first convert them into improper fractions. Improper fractions are those where the numerator is greater than or equal to the denominator (e.g., 5/2). Similarly, decimals can be converted into fractions for consistent application of the reciprocal rule.
Frequently Asked Questions (FAQ)
Q: What if I have a problem like 5/6 divided by 10?
A: The process is the same. Rewrite 10 as 10/1, flip 10/1 to 1/10, and then multiply: 5/6 x 1/10 = 5/60 = 1/12
Q: Can I use a calculator for this type of problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for solving more complex problems and for building a strong mathematical foundation.
Q: Why is it important to learn fraction division?
A: Mastering fraction division is essential for various mathematical applications and real-world scenarios. It improves problem-solving skills, logical reasoning, and builds confidence in tackling more advanced mathematical concepts.
Conclusion: Mastering Fraction Division
10 divided by 5/6 equals 12. This seemingly simple problem unveils the profound principles underlying fraction division. By understanding the concept of reciprocals and applying the step-by-step approach, you can confidently tackle similar problems and appreciate the beauty and practicality of fractional arithmetic. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you'll become. Don't hesitate to explore more complex examples and delve deeper into the rich world of mathematics. The journey of learning is continuous, and every step forward strengthens your mathematical abilities.
Latest Posts
Latest Posts
-
How Big Is Two Meters
Sep 23, 2025
-
How To Check Gas Mileage
Sep 23, 2025
-
1 Out Of 11 Percentage
Sep 23, 2025
-
71 Per Hour Annual Salary
Sep 23, 2025
-
Area Model Of Multiplication Worksheet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.