10 To The 23 Power
saludintensiva
Sep 20, 2025 · 7 min read
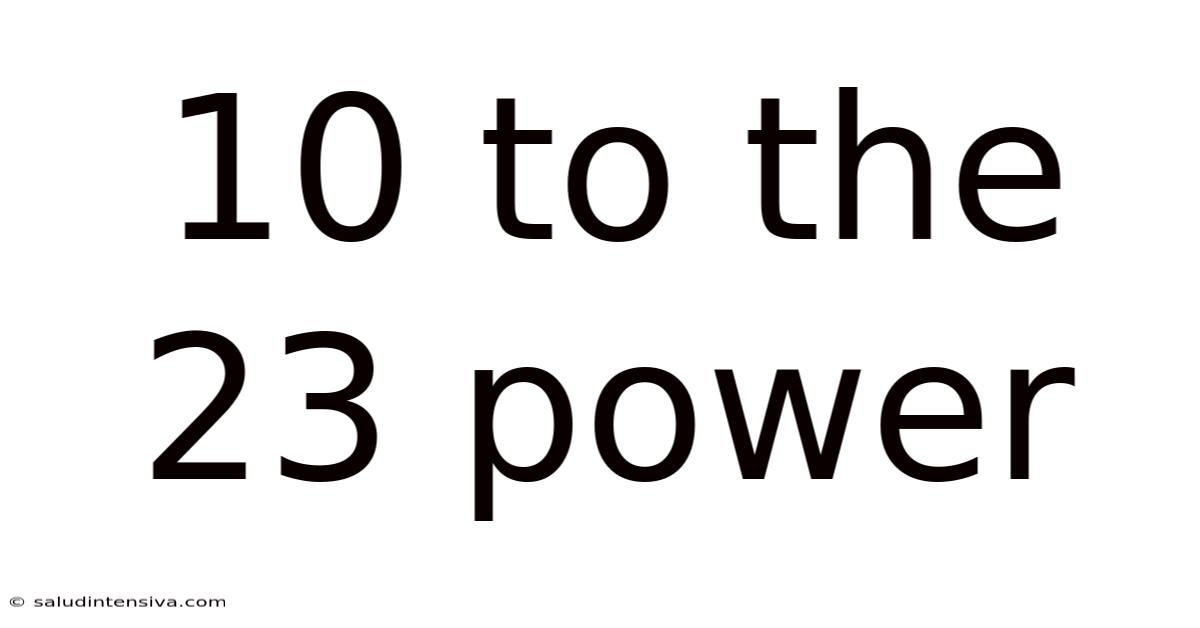
Table of Contents
Delving into the Immensity of 10<sup>23</sup>: A Journey into Avogadro's Number and Beyond
10<sup>23</sup>, or 10 to the 23rd power, is a number so vast it's difficult to truly comprehend. It's far beyond our everyday experiences of counting apples or cars. This number, however, holds significant importance in science, particularly in chemistry, where it represents a cornerstone concept: Avogadro's number. Understanding 10<sup>23</sup> means gaining insight into the scale of the atomic and molecular world, and the sheer magnitude of particles involved in even seemingly small quantities of matter. This article will explore this colossal number, its implications, and its connection to the fascinating world of moles and Avogadro's constant.
Understanding Scientific Notation and Exponential Growth
Before we dive into the specifics of 10<sup>23</sup>, let's briefly refresh our understanding of scientific notation. Scientific notation is a way of expressing very large or very small numbers concisely. It uses powers of 10 to represent the number. For example, 10<sup>3</sup> means 10 multiplied by itself three times (10 x 10 x 10 = 1000). Similarly, 10<sup>23</sup> means 10 multiplied by itself 23 times. This results in a number with 24 digits: 1 followed by 23 zeros (10,000,000,000,000,000,000,000). It's easier to visualize and manipulate large numbers using this notation. The exponent (the "23" in 10<sup>23</sup>) tells us the order of magnitude – how many times the number is multiplied by 10.
Exponential growth, represented by this notation, is a powerful concept that describes how quantities increase rapidly over time. It's not a linear increase, but rather a multiplicative one. Think of compound interest: the interest earned each year is added to the principal, and subsequent interest is calculated on a larger sum. Similarly, 10<sup>23</sup> showcases the enormous potential for growth through repeated multiplication.
Avogadro's Number: The Bridge to the Microscopic World
Avogadro's number, approximately 6.022 x 10<sup>23</sup>, is a fundamental constant in chemistry. It represents the number of constituent particles (atoms, molecules, ions, etc.) in one mole of a substance. A mole is a unit of measurement used in chemistry to express the amount of a substance. It's like saying "a dozen" (12) but on a much larger scale. Instead of 12 items, a mole contains approximately 6.022 x 10<sup>23</sup> items.
The significance of Avogadro's number lies in its ability to connect the macroscopic world (what we can see and measure directly) to the microscopic world of atoms and molecules. We can't directly count atoms, but we can measure the mass of a substance and use Avogadro's number to calculate the number of atoms or molecules present. This is crucial for stoichiometry, the branch of chemistry that deals with the quantitative relationships between reactants and products in chemical reactions.
Practical Applications of 10<sup>23</sup> and Avogadro's Number
The sheer magnitude of 10<sup>23</sup> and its close relation to Avogadro's number has profound implications across various scientific fields:
-
Chemistry: As previously mentioned, it's essential for stoichiometric calculations. Understanding moles and Avogadro's number allows chemists to accurately predict the amounts of reactants needed and products formed in chemical reactions. This is crucial in industrial processes, pharmaceutical development, and many other areas.
-
Physics: Avogadro's number plays a role in understanding the properties of gases and their behavior at the molecular level. It's used in calculations involving gas laws and the kinetic theory of gases.
-
Materials Science: The number of atoms in a material directly impacts its properties. Understanding the sheer number of atoms present allows material scientists to tailor materials with specific properties, such as strength, conductivity, or reactivity.
-
Environmental Science: Avogadro's number helps in analyzing environmental samples and determining the concentration of pollutants or other substances of interest. This is essential for environmental monitoring and pollution control.
-
Cosmology: While less directly involved, the concept of such massive numbers helps us appreciate the immense scale of the universe. Comparing the number of atoms in a grain of sand to the number of stars in the observable universe offers a perspective on the vastness of cosmic scales.
Illustrative Examples: Bringing the Scale into Perspective
It's hard to grasp the scale of 10<sup>23</sup>. Let's try some analogies:
-
Grains of Sand: Imagine a beach with countless grains of sand. It's estimated that there are approximately 10<sup>18</sup> grains of sand on all the beaches on Earth. That's a large number, but it's still 10<sup>5</sup> (100,000) times smaller than 10<sup>23</sup>.
-
Stars in the Milky Way: Our Milky Way galaxy contains an estimated 10<sup>11</sup> stars. To reach 10<sup>23</sup>, you would need 10<sup>12</sup> (one trillion) Milky Way galaxies.
-
Atoms in a Teaspoon of Water: A single teaspoon of water contains approximately 10<sup>23</sup> water molecules. This is roughly equal to Avogadro's number, showcasing the huge number of particles contained in even tiny amounts of matter.
These examples highlight the incomprehensible scale of 10<sup>23</sup>. It’s a number that transcends our everyday experiences, forcing us to grapple with the vastness of the universe and the microscopic world within.
Going Beyond 10<sup>23</sup>: Exploring Larger Numbers
While 10<sup>23</sup> is a massive number, it's just a small step on the scale of exponential growth. In various fields of science, even larger numbers are encountered. For example:
-
Number of Atoms in the Earth: The estimated number of atoms in the Earth is around 10<sup>50</sup>.
-
Number of Elementary Particles in the Observable Universe: Estimates for the number of elementary particles (protons, neutrons, electrons) in the observable universe reach into the range of 10<sup>80</sup>.
These examples demonstrate that 10<sup>23</sup>, while immense, is only a fraction of the scale of numbers that can be found in nature.
Frequently Asked Questions (FAQ)
-
Q: What is the exact value of Avogadro's number?
- A: The exact value of Avogadro's number is 6.02214076 × 10<sup>23</sup>. However, for most calculations, using 6.022 x 10<sup>23</sup> is sufficiently accurate.
-
Q: Why is Avogadro's number so important?
- A: Avogadro's number provides a bridge between the macroscopic world (grams, liters) and the microscopic world (atoms, molecules). It allows us to relate the measurable quantities to the actual number of particles involved.
-
Q: How can I visualize such a large number?
- A: It's difficult to truly visualize such a large number. Using analogies, as shown above, is one approach. Another is to consider that if you were to count one particle per second, it would take far longer than the age of the universe to count to 10<sup>23</sup>.
-
Q: Are there numbers larger than 10<sup>23</sup> in everyday life?
- A: Not in the context of everyday counting. However, the concepts of large numbers, represented in scientific notation, are crucial for understanding things like national debts, global populations, or the number of bytes of data on the internet.
Conclusion: Appreciating the Immensity and Significance
10<sup>23</sup> is a number that challenges our intuition and expands our understanding of scale. Its connection to Avogadro's number makes it a cornerstone in chemistry and many other scientific disciplines. By understanding this immense number, we gain a deeper appreciation for the vastness of the universe and the incredible complexity of matter at the atomic and molecular levels. While we might not be able to fully grasp its magnitude, recognizing its importance in our understanding of the world around us is a crucial step in appreciating the power of scientific measurement and the beauty of scientific exploration. The journey into the world of 10<sup>23</sup> is not just about numbers; it's a journey into the heart of matter itself.
Latest Posts
Latest Posts
-
52 60 As A Percentage
Sep 20, 2025
-
How To Find Diagonal Length
Sep 20, 2025
-
3 5 In Number Line
Sep 20, 2025
-
How Many Hours Is 3 75
Sep 20, 2025
-
Calculate Second Moment Of Area
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 To The 23 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.