10 X 7 X 3
saludintensiva
Sep 19, 2025 · 6 min read
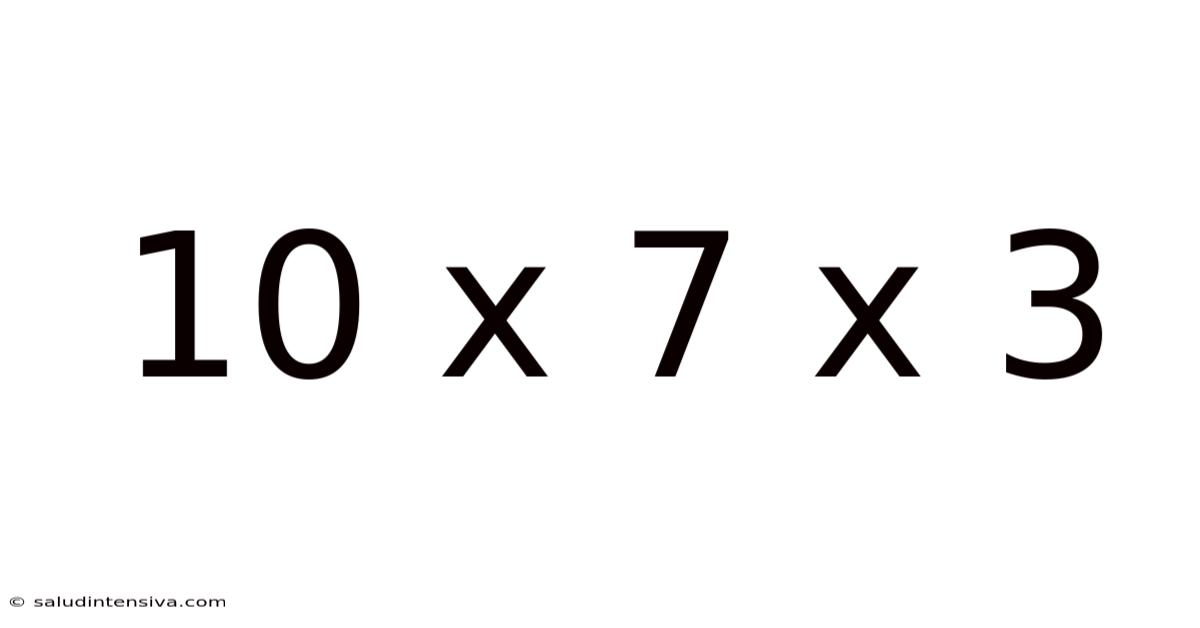
Table of Contents
Unveiling the Mysteries of 10 x 7 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "10 x 7 x 3," delving beyond the basic calculation to uncover its underlying principles, practical applications, and broader implications within mathematics and beyond. Understanding this seemingly simple equation provides a gateway to grasping more complex mathematical concepts and their real-world relevance. We'll unpack the process of multiplication, explore the properties of numbers involved, and even touch upon the historical context of such calculations. This comprehensive guide is suitable for students, educators, and anyone curious about the fascinating world of numbers.
Introduction: Beyond the Basic Calculation
At first glance, 10 x 7 x 3 appears straightforward. A quick calculation reveals the answer: 210. However, this seemingly simple equation offers a rich opportunity to explore fundamental mathematical concepts and their practical applications. We'll break down the calculation step-by-step, examine the properties of the numbers involved (10, 7, and 3), and discuss the various contexts in which such multiplications are used. We'll even explore how this seemingly simple calculation can be a stepping stone to understanding more complex mathematical ideas like algebra, geometry, and even calculus.
Step-by-Step Calculation: A Journey Through Multiplication
The calculation of 10 x 7 x 3 can be approached in several ways, highlighting the commutative and associative properties of multiplication. The commutative property states that the order of numbers in a multiplication doesn't affect the result (a x b = b x a). The associative property allows us to group numbers differently without changing the outcome ((a x b) x c = a x (b x c)).
Here are a couple of approaches:
-
Method 1: Left to Right: We start by multiplying 10 x 7 = 70. Then, we multiply the result by 3: 70 x 3 = 210.
-
Method 2: Grouping: We could choose to multiply 7 x 3 first, resulting in 21. Then we multiply 10 x 21 = 210. This showcases the associative property in action.
Both methods yield the same answer, emphasizing the flexibility and consistency within the rules of multiplication.
The Properties of 10, 7, and 3: A Number's Tale
Each of the numbers in our equation – 10, 7, and 3 – possess unique mathematical properties that contribute to the overall calculation:
-
10: This is a decimal number, forming the base of our number system. Its significance lies in its role as a power of 10 (10<sup>1</sup>), making multiplication by 10 relatively straightforward – simply adding a zero to the end of the other number.
-
7: This is a prime number, meaning it's only divisible by 1 and itself. Prime numbers are fundamental building blocks in number theory and have significant applications in cryptography and other fields.
-
3: Another important number, 3 is also a prime number. Its presence, along with 7, introduces a layer of prime factorization into our equation, which is crucial in advanced mathematical concepts.
Practical Applications: Where Does 10 x 7 x 3 Appear in Real Life?
The equation 10 x 7 x 3, while seemingly abstract, finds numerous applications in everyday life and various professional fields:
-
Measurement and Geometry: Imagine calculating the volume of a rectangular prism (box). If the prism has dimensions of 10 units, 7 units, and 3 units, then 10 x 7 x 3 calculates its volume (210 cubic units). This has implications in construction, packaging, and numerous other fields.
-
Business and Finance: Suppose a company sells a product for $7 each, and they sell 10 units per day for 3 days. The total revenue for those three days is calculated as 10 x 7 x 3 = $210. This simple calculation forms the foundation of inventory management, sales forecasting, and profit analysis.
-
Data Analysis and Statistics: In statistical calculations, often you'll encounter scenarios involving multiplying different data points. This equation could represent the total number of items across different categories or the total quantity of goods produced over several production cycles.
-
Everyday Scenarios: Think about arranging items: You might need to arrange 10 rows of 7 items each across 3 different tables. The total number of items will be 10 x 7 x 3 = 210.
Expanding the Horizons: Connections to Advanced Mathematics
The seemingly simple calculation of 10 x 7 x 3 serves as a foundational stepping stone to more complex mathematical concepts:
-
Algebra: This equation can be represented algebraically. Let's say x = 10, y = 7, and z = 3. The equation then becomes x * y * z = 210. This introduces the concept of variables and their manipulation in equations.
-
Geometry: As mentioned earlier, calculating volumes and areas relies heavily on multiplication. Understanding 10 x 7 x 3 helps lay the groundwork for more advanced geometric calculations involving three-dimensional shapes and more complex formulas.
-
Calculus: Although seemingly distant, the principles of multiplication underly many concepts in calculus, particularly integration and differentiation. The iterative nature of multiplication is mirrored in the summation and limit concepts central to calculus.
-
Number Theory: The use of prime numbers (7 and 3) in our equation allows us to explore concepts like prime factorization and divisibility rules, which are fundamental in number theory and cryptography.
Beyond the Numbers: The History of Multiplication
The history of multiplication is deeply intertwined with the development of civilization itself. Early civilizations used various methods for multiplication, from using physical objects for counting to developing sophisticated algorithms. The ancient Egyptians, Babylonians, and Greeks all contributed to the evolution of multiplication techniques. The development of positional number systems, like our decimal system, significantly simplified multiplication processes, paving the way for the complex calculations we perform today.
Frequently Asked Questions (FAQ)
Q: What if the order of the numbers changes? Will the answer be different?
A: No. Multiplication is commutative and associative. This means that changing the order of the numbers (10 x 3 x 7, 7 x 10 x 3, etc.) or how you group them ((10 x 7) x 3, 10 x (7 x 3), etc.) will not alter the final result, which will always be 210.
Q: Are there other ways to calculate 10 x 7 x 3 besides the methods mentioned?
A: Yes, you could use distributive property (breaking down numbers into simpler components) or use different multiplication algorithms (like lattice multiplication). The choice of method often depends on personal preference and the complexity of the numbers involved.
Q: What are some real-world examples beyond those mentioned in the article?
A: Consider cooking: If a recipe calls for 10 batches of cookies, each requiring 7 ounces of flour, and you need to make 3 times the recipe, then you will need 10 x 7 x 3 ounces of flour. Or, imagine calculating the total cost of 10 items, each costing $7, purchased from 3 different stores – 10 x 7 x 3 will give the total cost.
Conclusion: The Enduring Significance of 10 x 7 x 3
The simple equation 10 x 7 x 3, while seemingly basic, opens a window into the rich world of mathematics. It showcases fundamental concepts like multiplication, prime numbers, and the properties of numbers. Its applications extend far beyond a simple calculation, finding relevance in various aspects of life, from everyday tasks to complex scientific and engineering applications. This exploration encourages us to appreciate the interconnectedness of mathematical concepts and their profound influence on our understanding of the world around us. By understanding the underpinnings of this seemingly simple calculation, we gain a more robust foundation for tackling more complex mathematical challenges in the future. The journey from a simple equation to a vast expanse of mathematical knowledge demonstrates the power of curiosity and the beauty inherent in the study of numbers.
Latest Posts
Latest Posts
-
600 In Words For Check
Sep 20, 2025
-
Sum Of Five Squares Calculator
Sep 20, 2025
-
All The Factors Of 42
Sep 20, 2025
-
How Big Is 2 Yards
Sep 20, 2025
-
60 Days After June 21
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 X 7 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.