11/2 As A Mixed Number
saludintensiva
Sep 10, 2025 · 6 min read
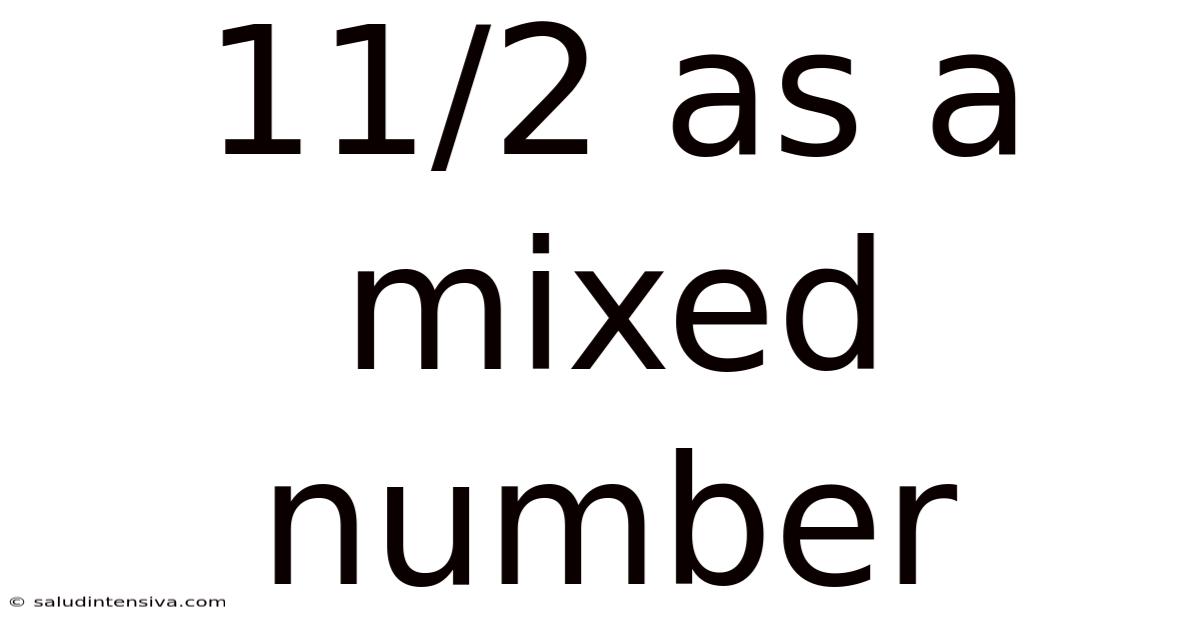
Table of Contents
Understanding 11/2 as a Mixed Number: A Comprehensive Guide
The fraction 11/2, while seemingly simple, presents a valuable opportunity to delve deeper into the world of fractions and mixed numbers. This article will not only explain how to convert 11/2 into a mixed number but also explore the underlying concepts, provide practical examples, and answer frequently asked questions. Understanding this conversion is crucial for mastering fundamental arithmetic skills and tackling more complex mathematical problems later on. We'll explore the meaning of improper fractions, the process of conversion, and its applications in real-world scenarios.
What is a Mixed Number?
Before we dive into converting 11/2, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number), like 1/2, 2/3, or 3/4. In contrast, an improper fraction has a numerator greater than or equal to its denominator, like 11/2, 5/4, or 9/9. Mixed numbers offer a more intuitive way to represent quantities larger than one. For example, 1 ½ is easier to visualize than 3/2.
Converting 11/2 to a Mixed Number: Step-by-Step Guide
The fraction 11/2 is an improper fraction because the numerator (11) is larger than the denominator (2). To convert it to a mixed number, we need to determine how many times the denominator (2) goes into the numerator (11) and what the remainder is. Here's the step-by-step process:
-
Division: Divide the numerator (11) by the denominator (2). 11 ÷ 2 = 5 with a remainder of 1.
-
Whole Number: The quotient (5) becomes the whole number part of the mixed number.
-
Fraction: The remainder (1) becomes the numerator of the fraction, and the denominator remains the same (2).
-
Mixed Number: Combining the whole number and the fraction, we get the mixed number 5 1/2.
Therefore, 11/2 as a mixed number is 5 1/2.
Visualizing the Conversion
Imagine you have 11 equally sized pieces of a pizza. If each whole pizza has 2 slices, how many whole pizzas and remaining slices do you have? You can make 5 complete pizzas (5 x 2 = 10 slices), and you’ll have 1 slice left over. This visually represents the mixed number 5 1/2.
Understanding the Process Mathematically
The conversion from an improper fraction to a mixed number is essentially a representation of division. The equation 11/2 = 5 1/2 can be understood as:
- 11 ÷ 2 = 5 with a remainder of 1
This remainder is then expressed as a fraction: 1/2 (remainder/denominator).
Converting Mixed Numbers back to Improper Fractions
It’s important to understand the reverse process as well. To convert a mixed number back to an improper fraction, follow these steps:
-
Multiply: Multiply the whole number by the denominator. (5 x 2 = 10)
-
Add: Add the result to the numerator of the fraction. (10 + 1 = 11)
-
Improper Fraction: This sum becomes the numerator of the improper fraction, while the denominator remains the same. (11/2)
This confirms that 5 1/2 is equivalent to 11/2.
Real-World Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life, making them an essential part of practical mathematics:
-
Measurement: Imagine measuring ingredients for a recipe. You might need 2 ½ cups of flour or 1 ¼ teaspoons of baking powder. Mixed numbers clearly communicate these quantities.
-
Time: Telling time often involves mixed numbers. For example, 2:30 is equivalent to 2 ½ hours.
-
Construction and Engineering: Precise measurements in construction and engineering often require the use of mixed numbers to represent dimensions and quantities.
-
Data Analysis: In situations where you have both whole numbers and fractions of units (like average scores, or parts of a whole), mixed numbers offer clear and concise representation.
Working with Mixed Numbers in Arithmetic
Adding, subtracting, multiplying, and dividing with mixed numbers requires understanding how to convert between mixed numbers and improper fractions. Generally, it's easier to perform these operations after converting the mixed numbers to improper fractions.
Addition and Subtraction: Convert mixed numbers to improper fractions, then perform the operation. Finally, convert the result back to a mixed number if needed.
Multiplication and Division: You can either convert mixed numbers to improper fractions before performing the operation or use the distributive property to multiply/divide the whole numbers and fractions separately. However, converting to improper fractions generally simplifies the process.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand mixed numbers?
A1: Mixed numbers provide a user-friendly way to represent quantities that are greater than one. Understanding their conversion to and from improper fractions is crucial for solving various mathematical problems in real-world scenarios, especially in measurement, time, and other quantitative applications.
Q2: Are there any other ways to represent 11/2?
A2: While 5 1/2 is the most common representation, you could also express it as a decimal (5.5) or as a percentage (550%). However, the mixed number form offers a clear understanding of the whole and fractional parts.
Q3: What if the remainder is zero after division?
A3: If the remainder is zero, it means the improper fraction is equivalent to a whole number. For example, 8/2 = 4. No fractional part is needed in this case.
Q4: Can I convert any improper fraction to a mixed number?
A4: Yes, any improper fraction can be converted to a mixed number by following the steps outlined above. The process involves dividing the numerator by the denominator and expressing the remainder as a fraction.
Q5: How do I simplify mixed numbers?
A5: Simplify the fractional part of the mixed number to its lowest terms. For example, if you have 2 4/6, you can simplify the fraction to 2/3, resulting in 2 2/3.
Conclusion
Converting 11/2 to a mixed number (5 1/2) is a fundamental skill in mathematics. This article has explained the process, provided visual and mathematical explanations, and explored its practical applications. Mastering this conversion allows you to confidently approach more complex mathematical problems and effectively handle quantitative information in various aspects of life. Understanding mixed numbers enhances your overall mathematical literacy and strengthens your problem-solving abilities, building a solid foundation for more advanced mathematical concepts in the future. Remember to practice regularly to solidify your understanding and build confidence in working with fractions and mixed numbers.
Latest Posts
Latest Posts
-
1 5 8 X 2
Sep 10, 2025
-
1 5 As A Percent
Sep 10, 2025
-
Rounding To The Nearest Millionth
Sep 10, 2025
-
Multiples Of 7 To 100
Sep 10, 2025
-
What Time Is 15 29
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 11/2 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.