11 20 As A Decimal
saludintensiva
Sep 18, 2025 · 6 min read
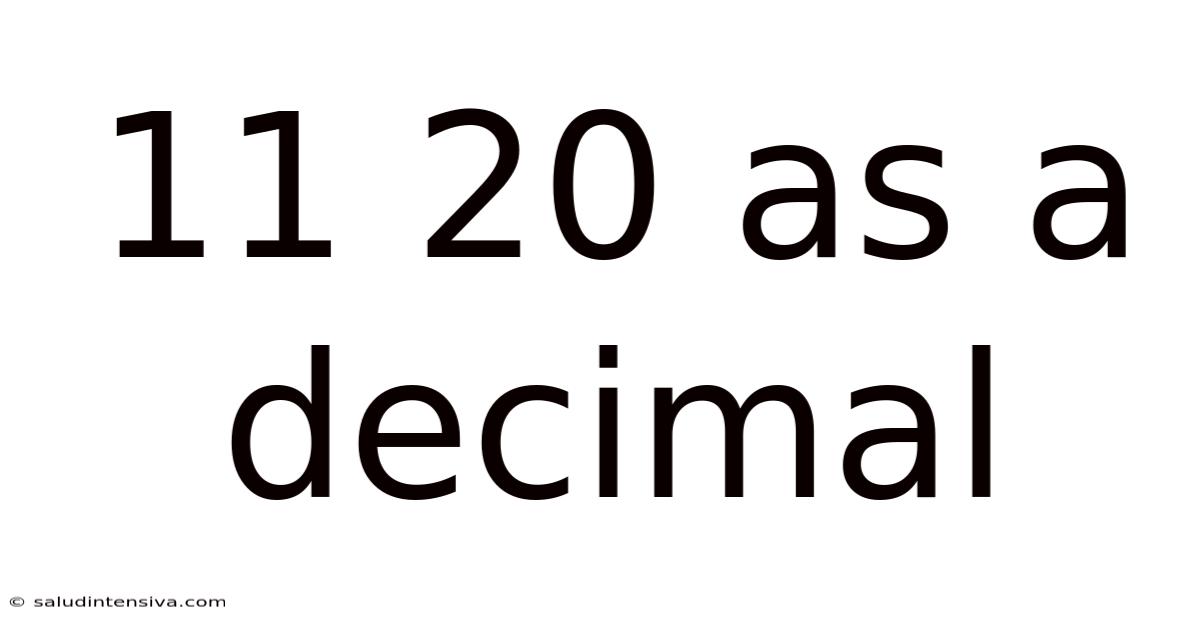
Table of Contents
Understanding 11/20 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to complex scientific computations. This article delves into the conversion of the fraction 11/20 to its decimal equivalent, providing a detailed explanation, various methods for solving it, and exploring the broader context of fraction-to-decimal conversions. We'll cover everything from the basic steps to more advanced concepts, ensuring a thorough understanding for learners of all levels.
Introduction: Why Convert Fractions to Decimals?
Fractions and decimals represent the same thing: parts of a whole. However, they offer different ways of expressing these parts. Decimals are particularly useful when performing calculations with a calculator or computer, and for comparing the relative size of fractional quantities. Understanding how to convert between fractions and decimals is therefore an essential skill in mathematics and its applications in science, engineering, and finance. This guide will focus specifically on the conversion of the fraction 11/20 to its decimal form, and we'll explore several methods to achieve this.
Method 1: Direct Division
The most straightforward method for converting a fraction to a decimal is through direct division. In this case, we need to divide the numerator (11) by the denominator (20):
11 ÷ 20 = 0.55
Therefore, 11/20 as a decimal is 0.55. This method is simple and intuitive, making it ideal for beginners. It involves performing the division using long division or a calculator.
Method 2: Converting to an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
This method involves finding an equivalent fraction where the denominator is a power of 10 (10, 100, 1000, and so on). This makes the conversion to a decimal much easier. To convert 11/20, we can multiply both the numerator and the denominator by 5:
(11 × 5) / (20 × 5) = 55/100
Since 55/100 means 55 hundredths, we can easily write this as a decimal: 0.55. This method highlights the relationship between fractions and decimals, illustrating how they represent the same value using different notations. The choice of multiplying by 5 is because 20 multiplied by 5 equals 100, a power of 10. This simplifies the conversion to a decimal.
Method 3: Understanding Place Value
Decimals are based on place value, similar to whole numbers but extending to the right of the decimal point. Each place value represents a power of 10. For example:
- 0.1 is one-tenth (1/10)
- 0.01 is one-hundredth (1/100)
- 0.001 is one-thousandth (1/1000) and so on.
Understanding this system is crucial for converting fractions to decimals and vice versa. By expressing 11/20 as 55/100, as shown in Method 2, we directly see that it represents 55 hundredths, hence the decimal 0.55. This approach emphasizes the fundamental principles behind decimal representation.
Method 4: Using a Calculator
Modern calculators readily perform fraction-to-decimal conversions. Simply enter the fraction 11/20 into your calculator, ensuring you use the correct input method (usually a division symbol). The calculator will directly provide the decimal equivalent: 0.55. While convenient, it's essential to understand the underlying mathematical principles, rather than solely relying on the calculator. This is because understanding the method helps in problem-solving scenarios where a calculator might not be readily available.
Further Exploration: Decimal Representation and its Significance
The decimal representation of 11/20, which is 0.55, is a terminating decimal. This means that the decimal representation ends after a finite number of digits. Not all fractions result in terminating decimals. For example, 1/3 results in a repeating decimal (0.333...). The denominator of the fraction determines whether the decimal representation will be terminating or repeating. Fractions with denominators that are only divisible by 2 and/or 5 result in terminating decimals. Any other factors in the denominator will lead to repeating decimals.
Expanding on Terminating and Repeating Decimals:
-
Terminating Decimals: These decimals have a finite number of digits after the decimal point. They can be expressed as a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000).
-
Repeating Decimals: These decimals have a sequence of digits that repeat infinitely. They are typically represented with a bar over the repeating sequence. For example, 1/3 = 0.3̅ (the bar indicates that the 3 repeats indefinitely). Repeating decimals can still be expressed as fractions.
The fact that 11/20 results in a terminating decimal is directly related to its denominator, 20, which is divisible by 2 and 5 (20 = 2² × 5).
Practical Applications of Decimal Conversions
Converting fractions to decimals is used extensively in various fields:
- Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Engineering: Precise measurements and calculations require the use of decimals.
- Science: Data analysis and scientific computations frequently involve decimal numbers.
- Everyday life: Calculating tips, splitting bills, or measuring ingredients in cooking often require converting fractions to decimals for ease of calculation.
Frequently Asked Questions (FAQ)
-
Q: Can any fraction be converted to a decimal?
- A: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. The resulting decimal may be terminating or repeating.
-
Q: What if the denominator of the fraction is a very large number?
- A: The same methods apply. Direct division or using a calculator will provide the decimal equivalent. However, the decimal might be very long and may require rounding for practical applications.
-
Q: Is there a quicker method than long division for some fractions?
- A: Yes, converting the fraction to an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.) offers a shortcut, as demonstrated in Method 2.
-
Q: How do I convert a repeating decimal back to a fraction?
- A: Converting repeating decimals to fractions involves algebraic manipulation. It's a slightly more advanced topic, but involves setting up an equation and solving for the fraction.
-
Q: Why is understanding decimal representation important?
- A: A strong grasp of decimal representation allows for efficient calculations, comparisons of quantities, and easier comprehension of data in various contexts. It is fundamental to further mathematical studies.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions to decimals is a crucial skill that underpins many mathematical applications. We have explored several methods for converting the fraction 11/20 to its decimal equivalent (0.55), highlighting the direct division method, the method of equivalent fractions with powers of 10 as denominators, the importance of understanding place value, and the convenience of using a calculator. Furthermore, we explored the distinction between terminating and repeating decimals, expanding on the factors that determine the nature of a fraction's decimal representation. By understanding these concepts and practicing the methods outlined, you can confidently tackle fraction-to-decimal conversions in various contexts, from simple calculations to more advanced mathematical problems. Remember, consistent practice is key to mastering this essential mathematical skill.
Latest Posts
Latest Posts
-
2 3 To The 3rd Power
Sep 18, 2025
-
Equivalent Fraction To 6 7
Sep 18, 2025
-
5 Minutes In An Hour
Sep 18, 2025
-
How To Simplify 3 4
Sep 18, 2025
-
Mean Of Grouped Data Calculator
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 11 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.