11 37 As A Percentage
saludintensiva
Sep 20, 2025 · 5 min read
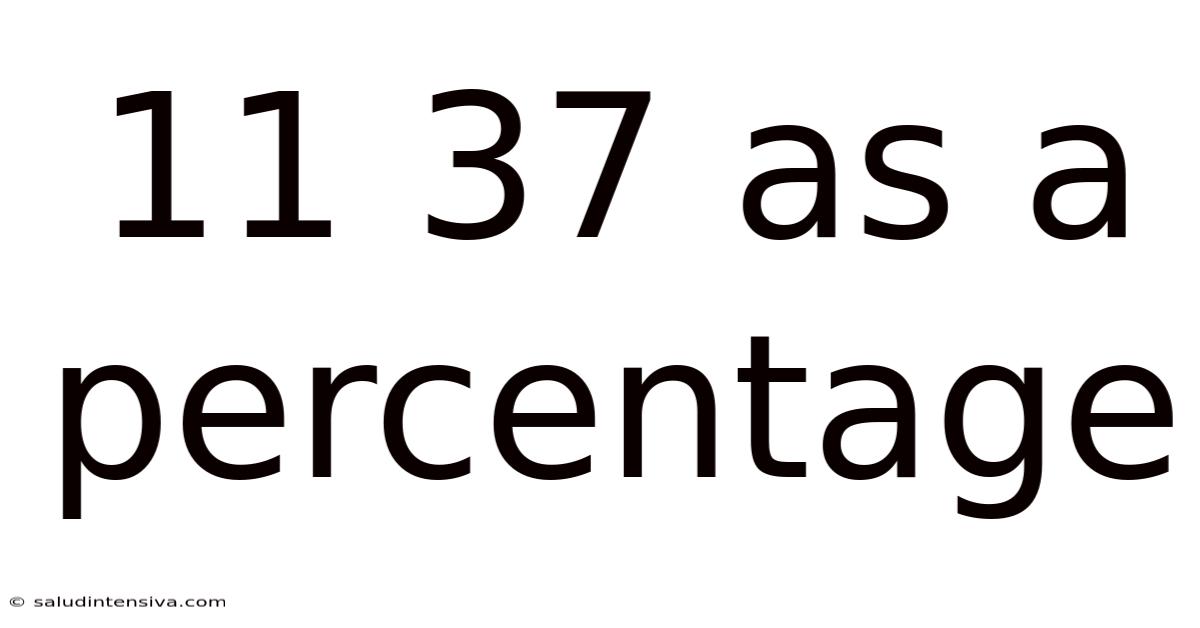
Table of Contents
Decoding 11/37 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts in a store to analyzing financial data. This article delves into the process of converting the fraction 11/37 into a percentage, explaining the methodology step-by-step and offering insights into related mathematical concepts. We'll also explore practical applications and address frequently asked questions to provide a complete understanding of this seemingly simple yet crucial calculation. By the end, you'll not only know the percentage equivalent of 11/37 but also grasp the underlying principles that allow you to tackle similar conversions confidently.
Understanding Fractions, Decimals, and Percentages
Before diving into the conversion of 11/37, let's refresh our understanding of the three interconnected concepts: fractions, decimals, and percentages.
-
Fractions: A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In 11/37, 11 is the numerator and 37 is the denominator.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on.
-
Percentages: Percentages represent a fraction or decimal as a proportion of 100. The symbol "%" signifies "per cent," meaning "out of one hundred."
These three concepts are interchangeable. A fraction can be converted into a decimal, and both can be converted into a percentage, and vice-versa. This inter-convertibility is crucial for performing various calculations and analyses.
Converting 11/37 into a Percentage: A Step-by-Step Guide
The process of converting 11/37 into a percentage involves two main steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case:
11 ÷ 37 ≈ 0.297297...
Notice that this decimal is a repeating decimal, meaning the sequence "297" repeats infinitely. For practical purposes, we'll round this decimal to a suitable number of decimal places. For this example, we'll use four decimal places, giving us 0.2973.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.2973 × 100 = 29.73%
Therefore, 11/37 is approximately 29.73%.
Understanding the Approximation
It's important to acknowledge that our answer is an approximation due to rounding the repeating decimal. The true value of 11/37 as a percentage has an infinitely repeating decimal representation. The level of accuracy needed depends on the context. For many purposes, 29.73% provides sufficient precision. However, in situations requiring higher accuracy, more decimal places should be retained.
Practical Applications of Percentage Conversions
The ability to convert fractions and decimals to percentages has a wide array of practical applications across diverse fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates.
-
Science: Representing experimental data, calculating probabilities, and expressing concentrations.
-
Business: Analyzing market share, sales growth, and cost reductions.
-
Everyday Life: Determining tips in restaurants, calculating sale prices, and understanding statistics in news reports.
Understanding percentage conversions allows for clearer comprehension and comparison of data, making informed decisions easier.
Exploring Related Mathematical Concepts
The conversion of 11/37 to a percentage highlights several fundamental mathematical concepts:
-
Ratio and Proportion: Fractions represent ratios, and percentages express proportions relative to 100.
-
Decimal Representation: Understanding the relationship between fractions and decimals is crucial for many mathematical operations.
-
Rounding and Approximation: The need for rounding illustrates the practical limitations of working with irrational numbers.
-
Repeating Decimals: The nature of the repeating decimal in this example introduces the concept of irrational numbers and their representation.
Frequently Asked Questions (FAQ)
Q1: Why is the decimal representation of 11/37 a repeating decimal?
A1: The decimal representation of 11/37 is a repeating decimal because the fraction cannot be simplified to a fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.). When the denominator contains prime factors other than 2 and 5, the decimal representation will often be a repeating decimal.
Q2: How can I increase the accuracy of the percentage calculation?
A2: To increase accuracy, retain more decimal places when rounding the decimal representation before converting to a percentage. Using a calculator or software that can handle repeating decimals without rounding will provide the most accurate result.
Q3: Are there other ways to convert a fraction to a percentage?
A3: Yes, another method involves finding an equivalent fraction with a denominator of 100. However, this method is not always practical, especially for fractions like 11/37 where finding an equivalent fraction with a denominator of 100 is difficult. The division method (dividing the numerator by the denominator) is generally more efficient and applicable to all fractions.
Q4: What if the fraction is an improper fraction (numerator > denominator)?
A4: If the fraction is improper, the resulting percentage will be greater than 100%. For example, if the fraction is 37/11, the decimal would be approximately 3.3636... which translates to approximately 336.36%. This represents a value more than the whole.
Q5: Can I use a calculator or software to perform this conversion?
A5: Yes, most calculators and mathematical software can easily perform this conversion. Simply enter 11/37 and convert it to a percentage using the calculator's built-in functions.
Conclusion
Converting 11/37 to a percentage, resulting in approximately 29.73%, involves a straightforward two-step process: converting the fraction to a decimal and then the decimal to a percentage. While the decimal representation of 11/37 is a repeating decimal, rounding to an appropriate number of decimal places provides a practical and sufficiently accurate percentage for most applications. Understanding this conversion process and its underlying principles is crucial for various applications across numerous fields, highlighting the importance of mastering basic mathematical concepts. Remember that the accuracy of your calculation is directly related to the number of decimal places you retain in your intermediate steps. Choose the level of precision that is appropriate for the context of your problem.
Latest Posts
Latest Posts
-
How Many Days Till 11 11
Sep 20, 2025
-
Convert 5 To A Fraction
Sep 20, 2025
-
The Square Root Of 30
Sep 20, 2025
-
Best 5 Card Plo Calculator
Sep 20, 2025
-
Meter Chart Smallest To Largest
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 11 37 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.