11 Out Of 25 Percentage
saludintensiva
Sep 13, 2025 · 5 min read
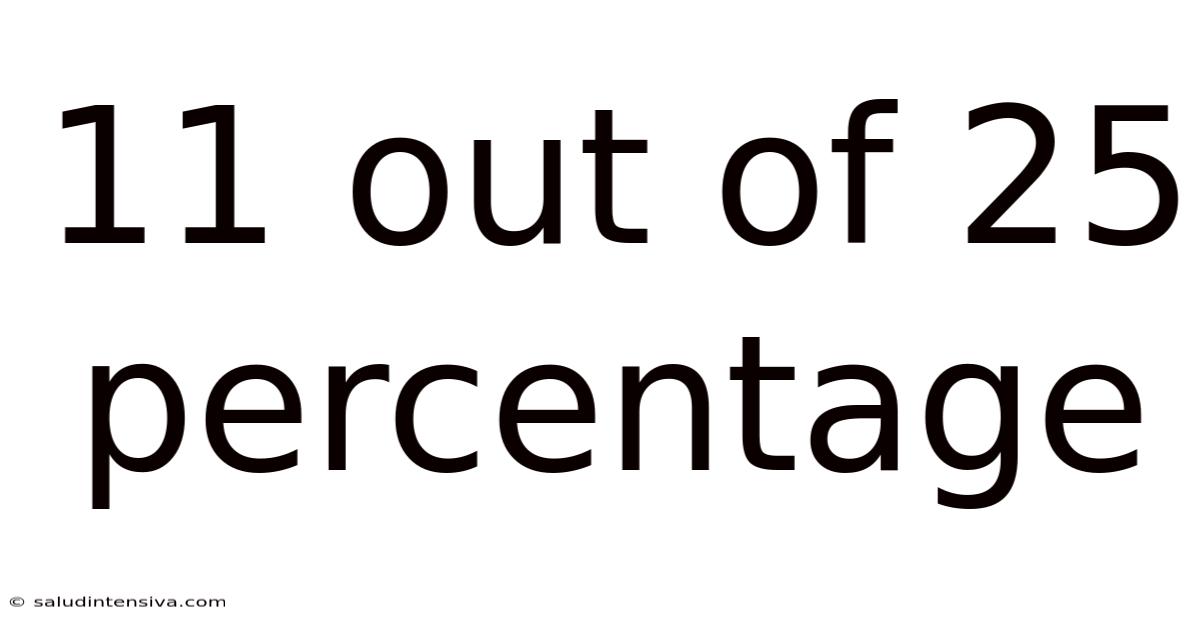
Table of Contents
Understanding 11 out of 25: A Comprehensive Guide to Percentages and Fractions
Calculating percentages is a fundamental skill used in various aspects of life, from academic assessments to financial transactions. Understanding how to interpret and calculate percentages allows you to make informed decisions and effectively communicate quantitative information. This article will delve into the intricacies of understanding "11 out of 25," explaining its percentage equivalent, the underlying mathematical principles, and practical applications. We'll also explore related concepts and frequently asked questions, providing a comprehensive resource for anyone seeking clarity on this topic.
What Does 11 out of 25 Mean?
The phrase "11 out of 25" represents a fraction where 11 is the numerator (the part) and 25 is the denominator (the whole). It indicates that 11 units are selected or achieved from a total of 25 possible units. This fraction can be expressed as 11/25. This simple expression forms the basis for calculating its percentage equivalent.
Calculating the Percentage: From Fraction to Percentage
To convert the fraction 11/25 into a percentage, we need to express it as a fraction with a denominator of 100. Here's how:
-
Set up the equation: We want to find the percentage, represented by 'x', such that: 11/25 = x/100
-
Solve for x: To solve for x, we can cross-multiply: 25x = 1100
-
Isolate x: Divide both sides by 25: x = 1100 / 25
-
Calculate the result: x = 44
Therefore, 11 out of 25 is equal to 44%.
Understanding the Concept of Percentage
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ( per centum in Latin). Percentages are used extensively because they provide a standardized and easily comparable way to represent proportions. For example, comparing a score of 11/25 to a score of 22/50 might be confusing initially, but converting both to percentages (44% and 44%) immediately clarifies that they represent the same proportion.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world situations, including:
-
Academic Performance: Calculating grades and understanding class rankings. A student scoring 11 out of 25 on a quiz would have achieved 44%.
-
Financial Matters: Calculating interest rates, discounts, tax rates, profit margins, and tips. Understanding percentage changes is crucial for budgeting and investment decisions. For instance, a 44% discount on a product.
-
Data Analysis: Interpreting statistical data, such as survey results, market research, and scientific experiments. Percentages help to visualize and compare proportions within datasets.
-
Everyday Life: Calculating sale prices, understanding nutritional information (percentage of daily value), and comparing prices of goods and services.
Beyond the Basics: Exploring Related Concepts
While understanding 11 out of 25 and its percentage equivalent is straightforward, let's explore some related concepts to deepen your understanding:
-
Decimals and Fractions: Percentages, decimals, and fractions are interchangeable. 44% can be written as the decimal 0.44 and the fraction 44/100 (which simplifies to 11/25). Understanding these conversions allows for flexibility in calculations.
-
Percentage Increase and Decrease: Calculating percentage changes involves comparing a new value to an original value. For example, if a value increases from 25 to 35, the percentage increase is calculated as [(35-25)/25] x 100% = 40%.
-
Compounding Percentages: This refers to the process of applying a percentage change repeatedly over time. It's frequently used in finance to calculate compound interest.
-
Weighted Averages: When different values contribute unequally to an overall result, weighted averages are used. This is common in academic grading where assignments might have different weightings.
Different Ways to Express the Same Proportion
Remember that 11/25 = 44/100 = 0.44 = 44%. These different forms represent the same proportion. Choosing the most appropriate form depends on the context. Fractions are useful for illustrating parts of a whole, decimals are convenient for calculations, and percentages are easy to interpret and compare.
Illustrative Examples: Real-world Scenarios
Let's consider some real-world scenarios where understanding 11 out of 25 (or 44%) is relevant:
-
A student's quiz score: A student answers 11 out of 25 questions correctly on a quiz. Their score is 44%.
-
A store sale: A store offers a 44% discount on all items. This means you pay 56% of the original price.
-
Market share: A company holds a 44% market share in a specific industry. This means they control 44% of the total market sales.
-
Survey results: In a survey of 25 respondents, 11 indicated preference for a particular product. This represents a 44% preference rate.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage from a fraction that doesn't easily simplify to a denominator of 100?
A1: Use the same method as described above: set up a proportion (fraction = x/100), cross-multiply, and solve for x. Alternatively, you can divide the numerator by the denominator and then multiply the result by 100%.
Q2: What if I need to calculate the percentage of something larger than 100?
A2: The method remains the same; the percentage can be greater than 100%. For example, if you have 125 out of 100, the percentage is 125%.
Q3: How do I calculate the percentage increase or decrease between two numbers?
A3: Find the difference between the two numbers. Divide the difference by the original number. Then, multiply the result by 100% to express it as a percentage.
Q4: Are there any online calculators available for percentage calculations?
A4: Yes, many online calculators are readily available to help you with percentage calculations. However, understanding the underlying principles is crucial for problem-solving.
Conclusion: Mastering Percentage Calculations
Understanding how to interpret and calculate percentages is a vital skill applicable across diverse domains. This article provided a comprehensive exploration of "11 out of 25," its percentage equivalent (44%), and related concepts. By mastering these calculations, you'll be equipped to tackle various real-world problems and make more informed decisions based on quantitative data. Remember that percentages, fractions, and decimals are all interconnected representations of proportions. Understanding these interrelationships empowers you to work with numerical data effectively and confidently. Practice regularly, and soon, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
Is 5 12 Bigger Than 1 2
Sep 13, 2025
-
5 To The 3th Power
Sep 13, 2025
-
5 8 Plus 5 8
Sep 13, 2025
-
Exponential Notation With Positive Exponents
Sep 13, 2025
-
3 X 5 X 2
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 25 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.