12 1000 As A Decimal
saludintensiva
Sep 21, 2025 · 5 min read
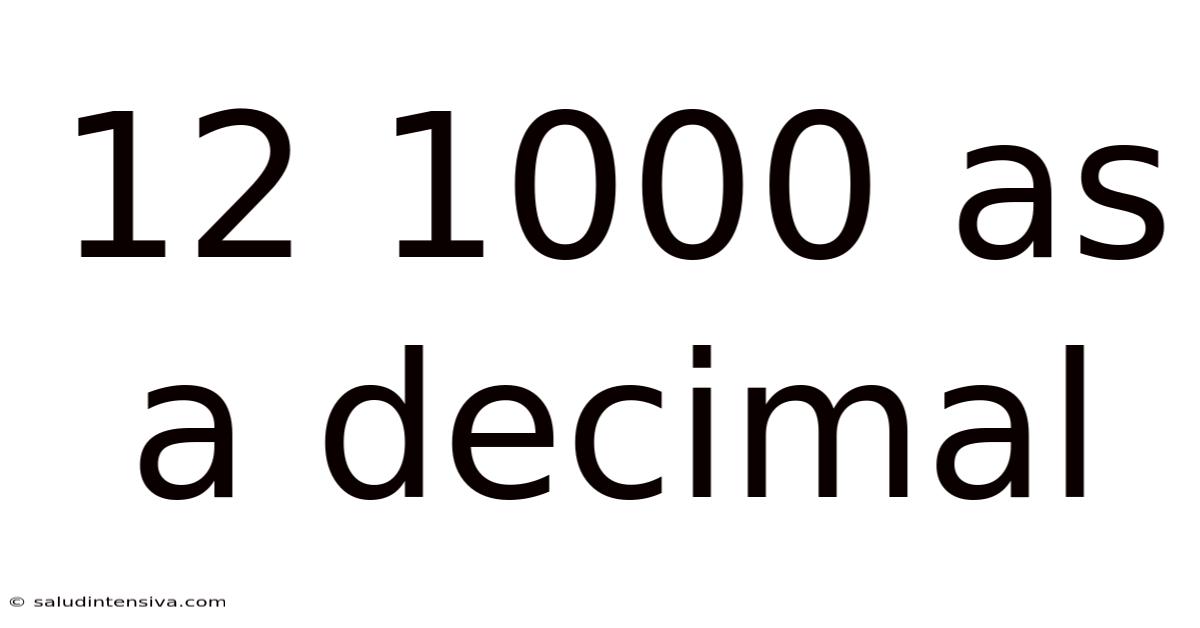
Table of Contents
Decoding 12/1000 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article delves deep into converting the fraction 12/1000 into its decimal form, explaining the process step-by-step, exploring the underlying principles, and addressing common questions. We’ll cover not only the mechanics of the conversion but also the broader context of decimal representation and its applications in various fields. This guide is designed for anyone seeking a thorough understanding of this seemingly simple yet crucial concept.
Introduction: Understanding Fractions and Decimals
Before we dive into the specifics of 12/1000, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 12/1000, 12 is the numerator and 1000 is the denominator. This means we have 12 parts out of a total of 1000 equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals use a decimal point (.) to separate the whole number part from the fractional part. For instance, 0.5 is a decimal representing 5/10 or one-half.
The ability to convert between fractions and decimals is essential for various mathematical operations and real-world applications, from calculating percentages to understanding financial data.
Converting 12/1000 to a Decimal: The Simple Method
The simplest way to convert 12/1000 to a decimal involves directly dividing the numerator (12) by the denominator (1000).
12 ÷ 1000 = 0.012
Therefore, the decimal equivalent of 12/1000 is 0.012. This is a straightforward calculation that can be performed using a calculator or manually through long division.
Understanding the Place Value System in Decimals
To further grasp the meaning of 0.012, let's examine the place value system in decimals. Each digit to the right of the decimal point represents a decreasing power of 10:
- 0.012
- The first digit after the decimal point (the tenths place) is 0.
- The second digit (the hundredths place) is also 0.
- The third digit (the thousandths place) is 2.
This signifies that we have 0 tenths, 0 hundredths, and 2 thousandths. Therefore, 0.012 can also be expressed as:
0 × (1/10) + 0 × (1/100) + 2 × (1/1000) = 2/1000 = 12/1000 (when simplified)
This reinforces the understanding that 0.012 is indeed the correct decimal representation of 12/1000.
Alternative Method: Using Equivalent Fractions
An alternative approach involves manipulating the fraction to have a denominator that is a power of 10. In this case, the denominator is already 1000, which is 10³. Therefore, no further manipulation is necessary. This method is particularly useful when the denominator isn't directly a power of 10. For example, if we had a fraction like 3/25, we could convert it to an equivalent fraction with a denominator of 100:
3/25 = (3 × 4) / (25 × 4) = 12/100 = 0.12
This demonstrates how converting to an equivalent fraction with a power-of-10 denominator simplifies the conversion to a decimal.
Practical Applications of Decimal Representation
Understanding decimal equivalents of fractions is crucial in many real-world applications:
- Finance: Calculating interest rates, discounts, and profit margins often involves working with decimal numbers.
- Measurement: Many measuring systems (metric system) use decimal values. For instance, converting centimeters to meters involves working with decimals.
- Science: Scientific measurements and calculations frequently utilize decimal notation for precision.
- Engineering: Designing and building structures and machines requires precise calculations, where decimals are essential.
- Data Analysis: Interpreting statistical data and representing it in graphs and charts often requires converting fractions to decimals.
Common Mistakes to Avoid
While the conversion of 12/1000 to a decimal seems simple, some common mistakes should be avoided:
- Misplacing the decimal point: Ensure the decimal point is correctly positioned. A misplaced decimal point can drastically alter the value.
- Incorrect division: Carefully perform the division of the numerator by the denominator to avoid errors. Double-checking your work is always advisable.
- Ignoring leading zeros: Leading zeros are crucial in indicating the place value of the digits. Omitting them can lead to misinterpretations. For instance, 0.012 is different from 0.12 or 1.2.
Frequently Asked Questions (FAQ)
Q1: Can 0.012 be simplified further?
A1: No, 0.012 is already in its simplest decimal form. While the fraction 12/1000 can be simplified to 3/250, this doesn't change the decimal equivalent.
Q2: How can I convert a decimal back to a fraction?
A2: To convert a decimal to a fraction, you write the decimal number as the numerator and a power of 10 as the denominator (determined by the number of digits after the decimal point). For example, 0.012 becomes 12/1000. Then you simplify the fraction to its lowest terms.
Q3: What if the fraction has a larger numerator?
A3: The same principle applies. Simply divide the numerator by the denominator. For example, if you have 125/1000, you would perform 125 ÷ 1000 = 0.125.
Q4: Are there other methods to convert fractions to decimals besides division?
A4: Yes, you can use equivalent fractions as explained earlier, or you can use long division. Long division is a more time-consuming method, but it provides a deeper understanding of the underlying principles.
Q5: What about fractions with denominators that are not powers of 10?
A5: For fractions with denominators that are not powers of 10, you would need to either find an equivalent fraction with a power of 10 denominator or use long division to get the decimal representation.
Conclusion: Mastering Decimal Conversions
Converting fractions to decimals, and vice versa, is a fundamental skill with wide-ranging applications. This article has thoroughly examined the conversion of 12/1000 to its decimal equivalent, 0.012, explaining the process through multiple methods and highlighting the underlying principles of place value and fraction simplification. Mastering this skill not only enhances mathematical proficiency but also enables a deeper understanding of numerical representation in various fields, from finance to science and engineering. Remember to practice regularly to build confidence and proficiency in handling fractions and decimals effectively. By understanding the fundamental concepts outlined here, you can confidently tackle more complex decimal conversions and further your mathematical knowledge.
Latest Posts
Latest Posts
-
Oil Tank Sizes For Homes
Sep 21, 2025
-
Convert 3 M To Inches
Sep 21, 2025
-
What Is 30 Of 49 99
Sep 21, 2025
-
One Thousand And Four Hundred
Sep 21, 2025
-
Expanded Form And Standard Form
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 1000 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.