12 15 In Simplest Form
saludintensiva
Sep 15, 2025 · 6 min read
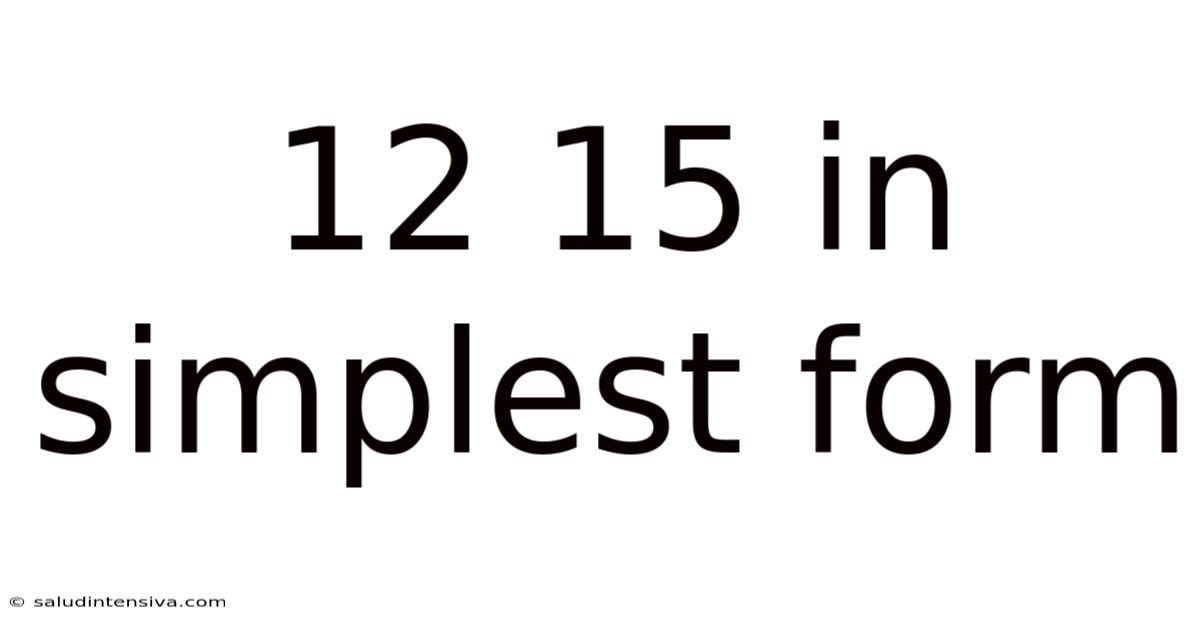
Table of Contents
Simplifying Fractions: A Deep Dive into 12/15
Understanding fractions is a fundamental building block in mathematics, paving the way for more complex concepts in algebra, calculus, and beyond. This article will explore the simplification of fractions, focusing specifically on the fraction 12/15. We'll delve into the process, explain the underlying mathematical principles, and address frequently asked questions, ensuring a comprehensive understanding for learners of all levels. This guide will equip you with the skills to simplify any fraction with confidence.
Introduction to Fraction Simplification
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it simply expresses it in a more concise and manageable form. Think of it like changing from quarters to a dollar – the value remains the same, only the representation changes.
Understanding the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. For example, the GCD of 12 and 15 is 3, because 3 is the largest number that divides both 12 and 15 evenly.
Simplifying 12/15 Step-by-Step
Let's break down the simplification of 12/15 step-by-step:
-
Find the factors of the numerator (12): The factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Find the factors of the denominator (15): The factors of 15 are 1, 3, 5, and 15.
-
Identify the common factors: Comparing the lists, we see that the common factors of 12 and 15 are 1 and 3.
-
Determine the Greatest Common Divisor (GCD): The largest common factor is 3. Therefore, the GCD of 12 and 15 is 3.
-
Divide both the numerator and denominator by the GCD: Divide both 12 and 15 by 3:
12 ÷ 3 = 4 15 ÷ 3 = 5
-
The simplified fraction: The simplified form of 12/15 is 4/5.
Alternative Methods for Finding the GCD
While the method above works well for smaller numbers, finding the GCD of larger numbers can be more time-consuming. Here are two alternative methods:
-
Prime Factorization: This method involves breaking down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- Prime factorization of 12: 2 x 2 x 3 (or 2² x 3)
- Prime factorization of 15: 3 x 5
The only common prime factor is 3. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide the larger number (15) by the smaller number (12): 15 ÷ 12 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 ÷ 3 = 4 with a remainder of 0.
- The last non-zero remainder is 3, so the GCD is 3.
Visual Representation of 12/15 and 4/5
Imagine you have a pizza cut into 15 equal slices. 12/15 represents having 12 of those slices. If you group those 12 slices into groups of 3, you'll have 4 groups. Similarly, if you regroup the entire pizza into groups of 5 slices each (by dividing the 15 slices into 3 groups of 5), then your 12 slices now represent 4 out of 5 groups of slices. This visually demonstrates that 12/15 and 4/5 represent the same amount.
The Importance of Simplifying Fractions
Simplifying fractions is crucial for several reasons:
-
Clarity and Ease of Understanding: Simplified fractions are easier to read and understand. 4/5 is clearly simpler and more intuitive than 12/15.
-
Easier Calculations: Simplifying fractions before performing operations like addition, subtraction, multiplication, or division makes the calculations much easier and less prone to errors.
-
Standard Form: Presenting answers in simplified form is a standard mathematical practice, ensuring consistency and clarity in communication.
-
Problem Solving: In real-world applications, simplifying fractions often leads to more practical and understandable solutions.
Applications of Fraction Simplification in Real Life
Fraction simplification isn't confined to the classroom; it's a practical skill used in numerous everyday situations:
-
Cooking and Baking: Following recipes often requires understanding and simplifying fractions to adjust ingredient quantities.
-
Construction and Engineering: Accurate measurements and calculations in construction and engineering often involve working with fractions.
-
Finance: Understanding fractions is essential for managing budgets, calculating percentages, and working with financial statements.
-
Data Analysis: Simplifying fractions can make data interpretation easier and clearer.
Frequently Asked Questions (FAQ)
Q: Can I simplify a fraction by only dividing the numerator?
A: No. To maintain the value of the fraction, you must divide both the numerator and the denominator by the same number (the GCD). Dividing only the numerator will change the value of the fraction.
Q: What if the numerator and denominator have no common factors other than 1?
A: The fraction is already in its simplest form.
Q: Is there a shortcut to simplifying fractions with larger numbers?
A: Using the prime factorization method or the Euclidean algorithm can be more efficient for larger numbers. Calculators with GCD functions can also be helpful.
Q: Why is simplifying fractions important in higher-level mathematics?
A: Simplified fractions make calculations significantly easier and reduce the chances of errors in more complex mathematical problems. This is crucial for accuracy and efficiency.
Q: What if I simplify a fraction and get a whole number?
A: That's perfectly acceptable. For instance, simplifying 6/3 results in 2, which is a whole number representing the simplified fraction.
Conclusion
Simplifying fractions, as demonstrated through the example of 12/15, is a fundamental skill in mathematics with far-reaching applications. Mastering this process enhances understanding, improves calculation efficiency, and ensures clarity in presenting mathematical solutions. By understanding the concept of the greatest common divisor and employing different methods to find it, you can confidently simplify any fraction and apply this valuable skill in various real-world contexts. Remember, practice makes perfect; the more you work with fractions, the more comfortable and proficient you'll become. Keep practicing, and you'll soon master this essential mathematical concept!
Latest Posts
Related Post
Thank you for visiting our website which covers about 12 15 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.