12 Divided By 3 4
saludintensiva
Sep 21, 2025 · 6 min read
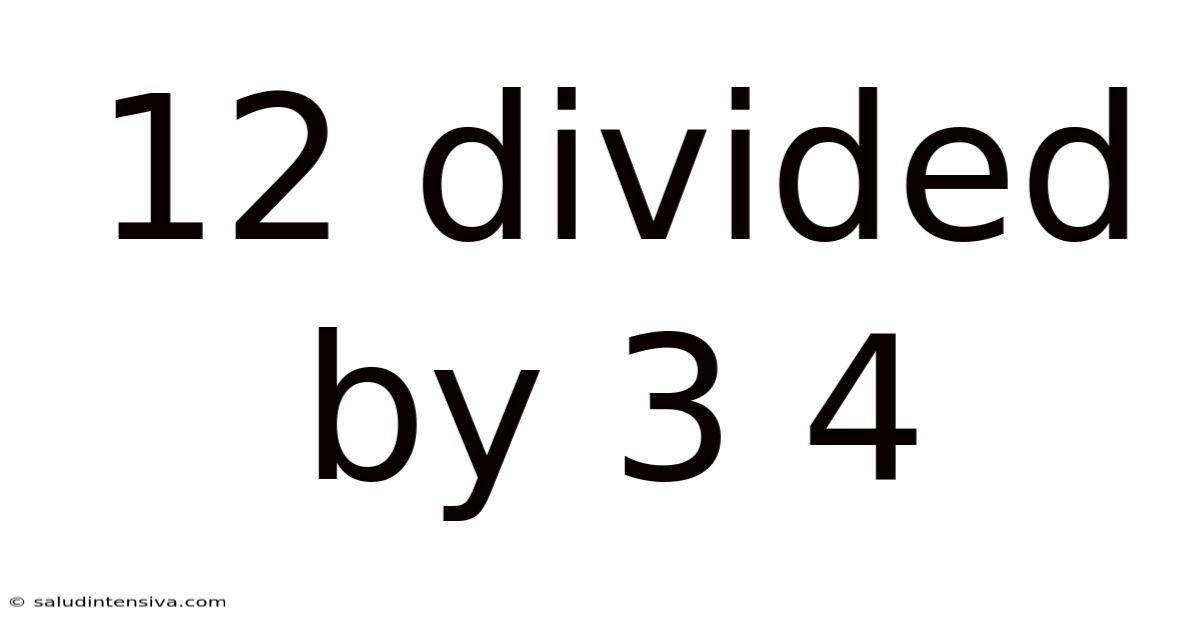
Table of Contents
Decoding 12 Divided by 3/4: A Deep Dive into Fractions and Division
This article will explore the seemingly simple yet conceptually rich problem of 12 divided by 3/4. We'll break down the process step-by-step, explaining the underlying mathematical principles and offering different approaches to solve the problem. Understanding this seemingly basic calculation is crucial for mastering fractions and lays a strong foundation for more advanced mathematical concepts. We will cover various methods, address common misconceptions, and provide a robust understanding of fraction division.
Introduction: Understanding Fraction Division
Dividing by a fraction is a common mathematical operation that often causes confusion. While it might seem counterintuitive at first, the process involves transforming the division problem into a multiplication problem. The key lies in understanding the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
This seemingly simple operation of flipping the fraction has profound implications in how we approach division problems involving fractions. Remember, dividing by a number is essentially asking "how many times does this number fit into the other number?" When we divide by a fraction, we're asking how many times a fraction fits into a whole number or another fraction. This is where the reciprocal comes in handy – it allows us to reframe the question in a more manageable way.
Method 1: The Reciprocal Method
The most straightforward approach to solving 12 divided by 3/4 is using the reciprocal method. This method involves converting the division problem into a multiplication problem by multiplying the dividend (12) by the reciprocal of the divisor (3/4).
Steps:
-
Identify the reciprocal: The reciprocal of 3/4 is 4/3.
-
Rewrite the problem as a multiplication problem: 12 ÷ (3/4) becomes 12 x (4/3).
-
Multiply the numerators and denominators: (12 x 4) / (1 x 3) = 48/3.
-
Simplify the fraction: 48/3 simplifies to 16.
Therefore, 12 divided by 3/4 equals 16.
This method is highly efficient and provides a clear, step-by-step process for solving division problems involving fractions. It's the preferred method for most students due to its simplicity and directness.
Method 2: Visual Representation with Models
While the reciprocal method provides a precise numerical solution, visualizing the problem can enhance understanding, especially for those who prefer a more intuitive approach. We can represent this problem using various models, such as circles or rectangles.
Imagine we have 12 whole circles. We want to divide these 12 circles into groups, where each group contains 3/4 of a circle. How many groups can we make?
Let's consider a single circle divided into four equal parts. 3/4 of a circle represents three of these parts. Since we have 12 whole circles, we can think of this as having 12 x 4 = 48 equal parts (each representing 1/4 of a circle). To find out how many 3/4 groups we can form, we divide 48 by 3: 48 / 3 = 16.
This visual method reinforces the concept of fraction division and illustrates why the reciprocal method works. It provides a tangible way to grasp the idea of how many times a fraction fits into a whole number.
Method 3: Converting to Improper Fractions
Another approach involves converting the whole number into a fraction before performing the division. This method might be more suitable for those comfortable working with improper fractions.
Steps:
-
Convert the whole number to a fraction: 12 can be written as 12/1.
-
Rewrite the division problem: (12/1) ÷ (3/4).
-
Apply the reciprocal method: (12/1) x (4/3).
-
Multiply the numerators and denominators: (12 x 4) / (1 x 3) = 48/3.
-
Simplify the fraction: 48/3 simplifies to 16.
This method showcases the versatility of fraction manipulation and reinforces the idea that whole numbers can be represented as fractions with a denominator of 1.
Explanation of the Mathematical Principles
The core principle behind dividing by a fraction involves the concept of reciprocals and the multiplicative inverse. Every non-zero number has a multiplicative inverse, which, when multiplied by the original number, results in 1. For fractions, the multiplicative inverse is its reciprocal.
When we divide by a fraction (a/b), we are essentially multiplying by its reciprocal (b/a). This is because division is the inverse operation of multiplication. Therefore, dividing by a fraction is equivalent to multiplying by its reciprocal. This fundamental principle underpins all the methods discussed above.
Addressing Common Misconceptions
A frequent mistake is simply dividing the whole number by the numerator and the denominator separately. This approach is incorrect because it doesn't accurately reflect the concept of dividing by a fractional part. Remember, dividing by a fraction means finding out how many times that fraction fits into the whole number.
Another common error is forgetting to simplify the resulting fraction. After performing the multiplication step, always check if the resulting fraction can be simplified to its lowest terms. This ensures an accurate and concise final answer.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for developing a strong mathematical foundation.
-
Q: What if the whole number was a decimal instead of an integer? A: You would follow the same process. Convert the decimal to a fraction, find the reciprocal of the divisor, and then multiply.
-
Q: Are there other ways to solve this problem? A: While the methods described above are the most efficient, you could also visualize it using a number line or other graphical representations.
-
Q: Why is the reciprocal method so effective? A: Because it converts a more complex division problem into a simpler multiplication problem, making it easier to calculate and understand.
Conclusion: Mastering Fraction Division
Solving 12 divided by 3/4, while seemingly straightforward, provides a valuable opportunity to solidify our understanding of fraction division and related mathematical principles. The various methods discussed – the reciprocal method, the visual representation method, and the method involving converting to improper fractions – all illustrate the same fundamental concept: dividing by a fraction is equivalent to multiplying by its reciprocal. Mastering this concept is critical for success in algebra, calculus, and many other areas of mathematics and science. By understanding and practicing these methods, you will build a stronger foundation in mathematics and develop greater confidence in tackling more complex problems in the future. Remember to practice regularly, explore different approaches, and always strive for a deep understanding of the underlying principles. This will help you not just solve problems, but truly master them.
Latest Posts
Latest Posts
-
Area Of Irregular Shape Calculator
Sep 21, 2025
-
Inches To Decimal Feet Conversion
Sep 21, 2025
-
60 Vs 100 Watt Bulb
Sep 21, 2025
-
3 To The Power 11
Sep 21, 2025
-
Oil Tank Sizes For Homes
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.