150 Percent As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
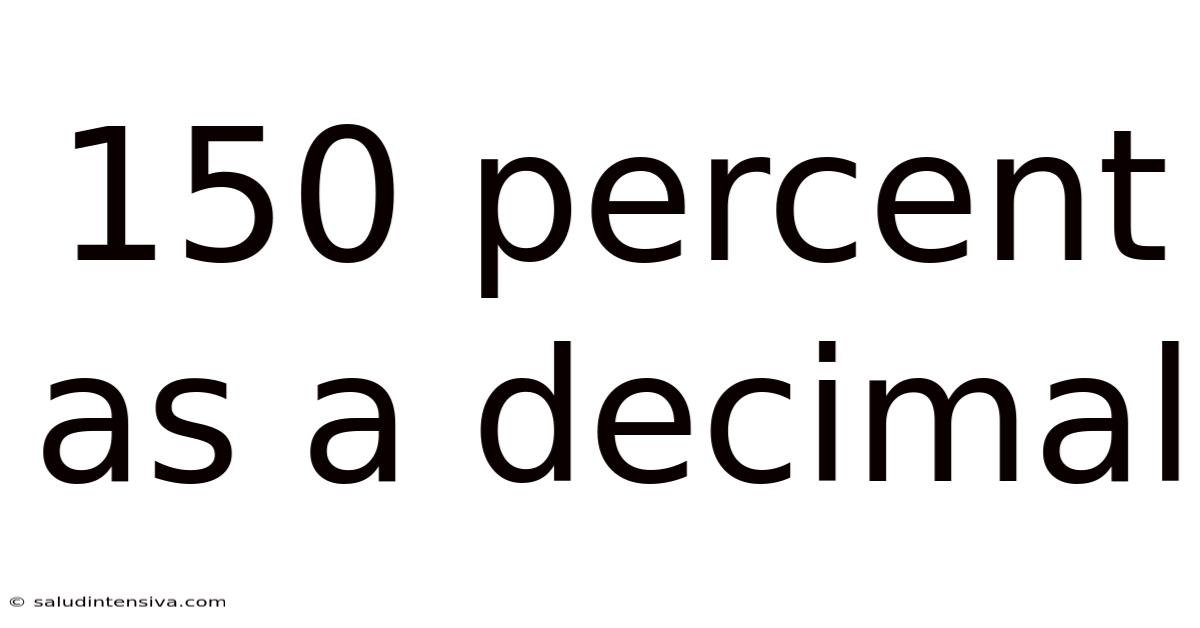
Table of Contents
150 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is fundamental to various fields, from finance and accounting to science and everyday calculations. This comprehensive guide will delve into the conversion of 150 percent to a decimal, explaining the process step-by-step and exploring its applications in different contexts. We'll also tackle common misconceptions and address frequently asked questions, ensuring a complete understanding of this seemingly simple yet crucial concept.
Understanding Percentages and Decimals
Before we dive into converting 150 percent, let's establish a solid foundation. A percentage represents a fraction of 100. For instance, 50 percent means 50 out of 100, or 50/100. A decimal, on the other hand, is a way of expressing a number using a base-ten system, with a decimal point separating the whole number from its fractional part. For example, 0.5 is a decimal representing one-half.
The relationship between percentages and decimals is crucial. To convert a percentage to a decimal, you simply divide the percentage by 100. Conversely, to convert a decimal to a percentage, you multiply the decimal by 100.
Converting 150 Percent to a Decimal
Now, let's tackle the main topic: converting 150 percent to its decimal equivalent. Following the established rule, we divide 150 by 100:
150 ÷ 100 = 1.5
Therefore, 150 percent as a decimal is 1.5. This means that 150% represents 1 and a half times the original value.
Practical Applications of 1.5 as a Decimal
The decimal equivalent of 150 percent, 1.5, finds numerous applications across various fields:
-
Finance and Investments: If an investment grows by 150 percent, its new value is 1.5 times its original value. For example, an initial investment of $100 would become $100 x 1.5 = $150. This is frequently used in calculating returns on investment (ROI) and compound interest.
-
Sales and Marketing: A 150 percent increase in sales indicates significantly improved performance compared to a previous period. Businesses use this metric to track growth and assess marketing campaign effectiveness.
-
Science and Engineering: In scientific calculations and engineering designs, percentages and decimals are often used interchangeably. A 150 percent increase in pressure, for instance, could translate to a 1.5-fold increase in the actual pressure value.
-
Everyday Calculations: Even in everyday life, understanding the decimal equivalent of 150 percent can be helpful. If a recipe calls for 150 percent of a particular ingredient, you would use 1.5 times the amount specified.
-
Data Analysis and Statistics: In statistical analysis, percentages are often converted to decimals for calculations. For instance, calculating mean, standard deviation, and other statistical parameters often requires working with decimal representations of percentages.
Working with Percentages Greater Than 100%
It's important to note that percentages can exceed 100 percent. This represents an increase beyond the original value. Understanding percentages greater than 100% is crucial in scenarios where growth or increase is substantial. For example:
-
Population Growth: A town whose population increases by 150% experiences more than a doubling in its population size.
-
Economic Growth: A country experiencing 150% GDP growth has more than doubled its economic output.
-
Stock Market Returns: A stock investment that yields a 150% return has more than doubled in value.
In all these examples, the decimal equivalent (1.5) plays a vital role in quantitative analysis and calculations.
Common Misconceptions about Percentages
Several misconceptions surround percentages, particularly those exceeding 100 percent:
-
Thinking Percentages are always between 0 and 100: This is a common mistake. Percentages can extend beyond 100%, representing an increase over the original value.
-
Difficulty in visualizing percentages greater than 100%: While it might be easier to visualize percentages within the 0-100 range, understanding that a percentage above 100 represents a multiplicative increase rather than just a portion of 100 helps in understanding the concept.
-
Incorrect conversion to decimals: A common error is forgetting to divide by 100 when converting a percentage to a decimal. Remember, the process always involves division by 100.
Further Exploration: Fractions, Decimals, and Percentages
Understanding the interrelationship between fractions, decimals, and percentages is essential for mastering this core mathematical concept. Here's a brief recap:
-
Fraction to Decimal: Divide the numerator by the denominator. For example, 3/4 = 0.75
-
Decimal to Fraction: Express the decimal as a fraction with a denominator as a power of 10 (e.g., 0.75 = 75/100). Then simplify the fraction if possible (75/100 simplifies to 3/4).
-
Fraction to Percentage: Convert the fraction to a decimal, then multiply by 100 and add the "%" symbol. For example, 3/4 = 0.75, which is 75%.
-
Percentage to Fraction: Divide the percentage by 100 and express the result as a fraction. For example, 75% = 75/100 = 3/4.
Mastering these conversions allows for seamless movement between different representations of the same numerical value, increasing your mathematical fluency.
Frequently Asked Questions (FAQ)
Q1: Can a percentage be more than 100%?
A1: Yes, absolutely. A percentage greater than 100% indicates an increase beyond the original value.
Q2: How do I convert a percentage to a decimal quickly?
A2: Divide the percentage by 100. For example, 150% ÷ 100 = 1.5
Q3: What are some real-world examples of percentages greater than 100%?
A3: Population growth, economic growth, stock market returns, and inflation are common examples.
Q4: Is 1.5 the same as 150%?
A4: Yes, 1.5 is the decimal equivalent of 150%.
Q5: What is the importance of understanding the decimal equivalent of 150%?
A5: Understanding the decimal equivalent enables precise calculations in various applications like finance, science, and everyday life. It allows for easier calculations within equations and formulas.
Conclusion
Converting 150 percent to a decimal, resulting in 1.5, is a fundamental mathematical operation with far-reaching applications. Understanding this conversion, and the broader concept of the relationship between percentages and decimals, is essential for success in numerous fields. By grasping the core principles discussed in this guide, you can confidently tackle percentage-related problems and confidently apply this knowledge to real-world situations. Remember to practice these conversions regularly to solidify your understanding and improve your mathematical proficiency. The ability to seamlessly convert between percentages and decimals is a valuable skill that will serve you well throughout your academic and professional pursuits.
Latest Posts
Latest Posts
-
What Are Multiples Of 15
Sep 10, 2025
-
4 3 8 As A Decimal
Sep 10, 2025
-
How To Simplify Negative Fractions
Sep 10, 2025
-
5 To The 4th Power
Sep 10, 2025
-
1 15 Random Number Generator
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 150 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.