16/12 As A Mixed Number
saludintensiva
Sep 11, 2025 · 6 min read
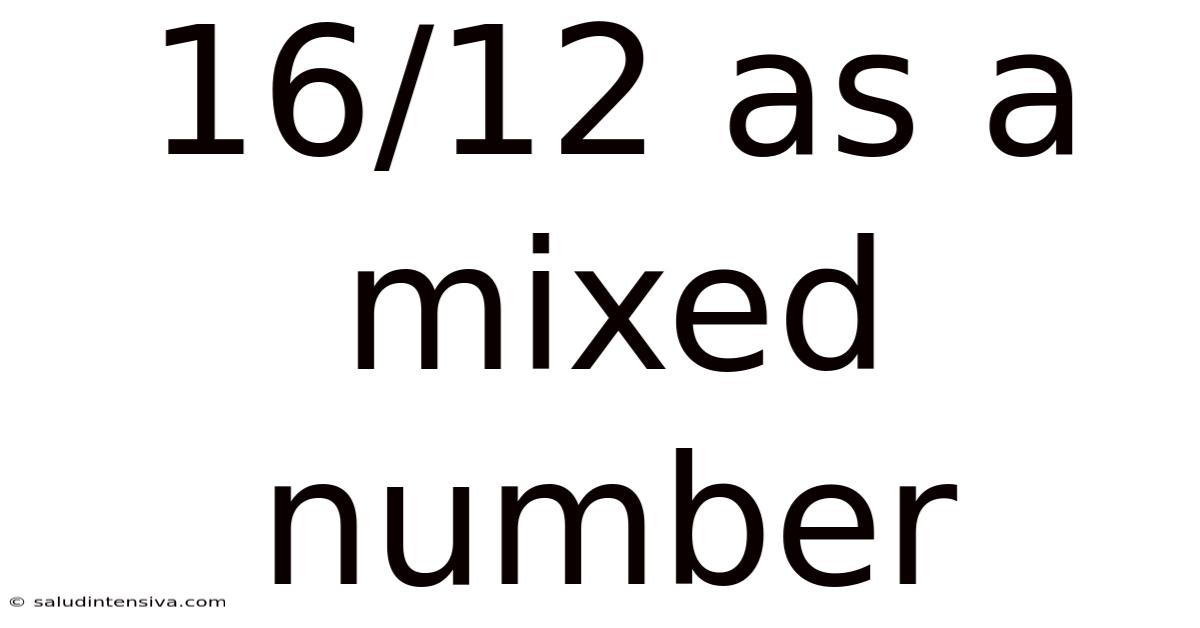
Table of Contents
Understanding 16/12 as a Mixed Number: A Comprehensive Guide
The fraction 16/12 represents a value greater than one. Understanding how to convert improper fractions like 16/12 into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will walk you through the process, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll delve into the definition of mixed numbers, explore different methods for conversion, and address frequently asked questions. By the end, you'll be confident in converting improper fractions to mixed numbers and vice-versa.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ²/₇ are all mixed numbers. They represent a quantity that's more than one whole unit, but not a complete whole number.
Converting 16/12 to a Mixed Number: The Step-by-Step Process
The core concept behind converting an improper fraction (like 16/12) to a mixed number involves dividing the numerator by the denominator. Here's a detailed breakdown of the steps:
-
Divide the Numerator by the Denominator: Divide 16 by 12. This gives you a quotient (the whole number part of your mixed number) and a remainder (which will become the numerator of the fractional part).
16 ÷ 12 = 1 with a remainder of 4
-
Identify the Whole Number: The quotient from the division is your whole number. In this case, the quotient is 1.
-
Identify the Numerator of the Fraction: The remainder from the division becomes the numerator of the fractional part of your mixed number. Here, the remainder is 4.
-
Keep the Original Denominator: The denominator of the fraction in your mixed number remains the same as the denominator of the original improper fraction. So, the denominator stays as 12.
-
Combine the Whole Number and the Fraction: Put the whole number and the fraction together to form your mixed number.
Therefore, 16/12 as a mixed number is 1 ⁴⁄₁₂
Simplifying the Fraction: A Crucial Step
While 1 ⁴⁄₁₂ is a correct mixed number representation of 16/12, we can simplify the fractional part. Both 4 and 12 are divisible by 4. Simplifying the fraction involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
-
Find the GCD of 4 and 12: The greatest common divisor of 4 and 12 is 4.
-
Divide the Numerator and Denominator by the GCD: Divide both 4 and 12 by 4.
4 ÷ 4 = 1 12 ÷ 4 = 3
-
Write the Simplified Mixed Number: The simplified mixed number is 1 ⅓
Alternative Method: Using Long Division
For larger numbers, long division can provide a clearer approach. Let's revisit the conversion of 16/12 using long division:
1
12 | 16
-12
---
4
The quotient (1) becomes the whole number, and the remainder (4) becomes the numerator of the fraction, keeping the original denominator (12). This again yields 1 ⁴⁄₁₂ which simplifies to 1 ⅓.
Visual Representation: Understanding Fractions and Mixed Numbers
Imagine you have 16 pizzas, each sliced into 12 equal pieces. The fraction 16/12 means you have 16 of these slices. You can assemble a complete pizza (12 slices) and still have 4 slices left. This visually represents the mixed number 1 ⁴⁄₁₂. Simplifying this, you have one whole pizza and one-third of another.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process. To convert a mixed number (like 1 ⅓) back to an improper fraction, follow these steps:
-
Multiply the Whole Number by the Denominator: Multiply 1 by 3, which equals 3.
-
Add the Numerator: Add the result (3) to the numerator of the fraction (1), giving you 4.
-
Keep the Original Denominator: The denominator remains the same (3).
-
Write the Improper Fraction: This gives you the improper fraction ⁴⁄₃.
Practical Applications of Converting Fractions to Mixed Numbers
Understanding the conversion between improper fractions and mixed numbers is essential in various real-world scenarios:
-
Cooking and Baking: Many recipes use fractional measurements. Converting improper fractions to mixed numbers makes it easier to understand quantities. For example, a recipe calling for 16/12 cups of flour is more easily understood as 1 ⅓ cups.
-
Measurement and Construction: Projects involving measurements often require working with fractions. Converting improper fractions simplifies calculations and interpretations.
-
Data Analysis and Statistics: Representing data using fractions is common. Using mixed numbers can offer a clearer understanding of the data, especially when presenting findings.
-
Everyday Life: Dividing things fairly often leads to fractional parts. Understanding mixed numbers allows for a clear understanding of the outcome.
Frequently Asked Questions (FAQ)
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, it means the original fraction was already a whole number. For instance, 12/12 = 1. There is no fractional part.
Q: Can I simplify before converting to a mixed number?
A: Yes, you can simplify the fraction before converting it to a mixed number. This often simplifies the division process and makes it easier to calculate the whole number and the fractional part. For example, simplifying 16/12 to 4/3 before division makes the process much easier.
Q: Why is simplifying the fraction important?
A: Simplifying fractions makes the number easier to understand and work with. It gives the same value in a more concise and manageable form.
Q: What if the fraction is already a proper fraction (e.g., 1/2)?
A: Proper fractions don't need to be converted to mixed numbers because they already represent a value less than one.
Q: Are there any other methods to convert improper fractions to mixed numbers?
A: While the division method is the most common, other visual or manipulative methods can be helpful, particularly for younger learners. For example, using fraction circles or other visual aids can make the concept clearer.
Conclusion: Mastering Improper Fractions and Mixed Numbers
Converting improper fractions like 16/12 to mixed numbers (and vice-versa) is a fundamental skill that builds a strong foundation in mathematics. Understanding the underlying principles, practicing the steps, and applying the knowledge to real-world situations will improve your mathematical proficiency significantly. By mastering this conversion, you'll be better equipped to tackle more complex mathematical challenges. Remember to always simplify your final answer for clarity and efficiency. Keep practicing, and you’ll quickly become proficient in working with mixed numbers and improper fractions!
Latest Posts
Latest Posts
-
Fractions Equivalent To 3 8
Sep 11, 2025
-
Improper Fraction Of 4 2 3
Sep 11, 2025
-
What Is 4 Of 18000
Sep 11, 2025
-
When Was 60 Days Ago
Sep 11, 2025
-
Convert 81 F To C
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 16/12 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.