16/7 As A Mixed Number
saludintensiva
Sep 19, 2025 · 5 min read
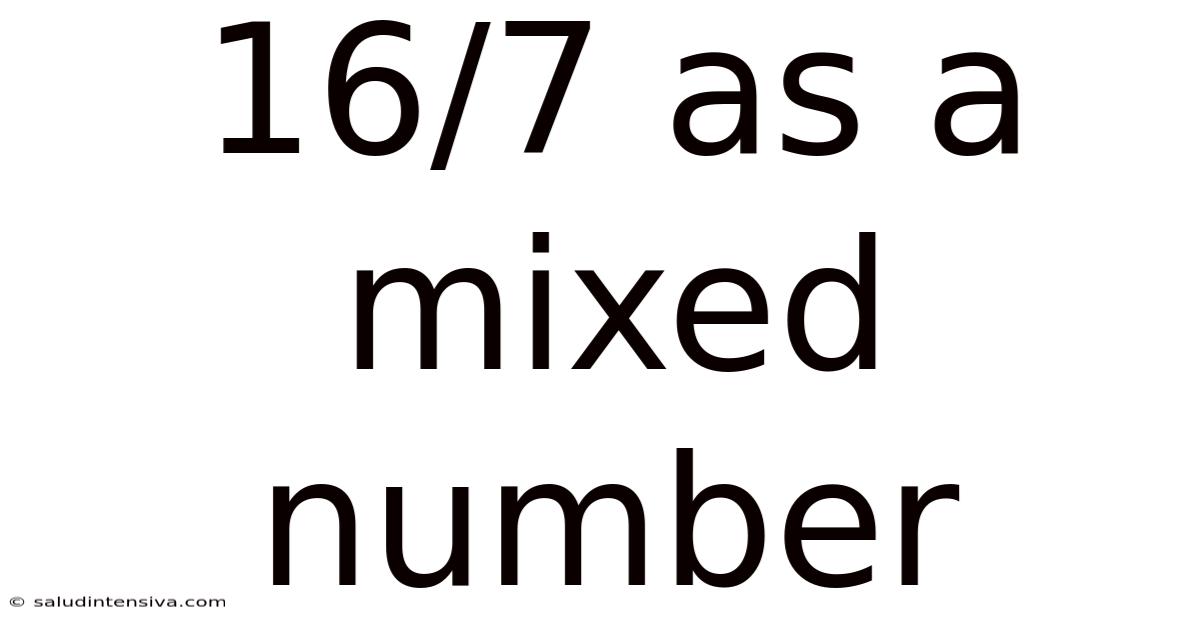
Table of Contents
Understanding 16/7 as a Mixed Number: A Comprehensive Guide
The seemingly simple fraction 16/7 holds a wealth of mathematical understanding within its seemingly small form. This article will comprehensively explore how to convert the improper fraction 16/7 into a mixed number, explaining the underlying principles in a clear and accessible manner, suitable for students of all levels. We will delve into the concept of mixed numbers, the process of conversion, and explore related applications. This guide will equip you with a solid understanding of this fundamental mathematical concept.
What is a Mixed Number?
Before diving into the conversion of 16/7, let's establish a clear understanding of what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ½, 3 ⁴⁄₅, and 1 ¹⁄₃ are all mixed numbers. They represent quantities that are greater than one whole unit.
Converting 16/7 to a Mixed Number: A Step-by-Step Approach
The process of converting an improper fraction (where the numerator is larger than or equal to the denominator) like 16/7 into a mixed number involves dividing the numerator by the denominator. Here's how it works:
-
Divide the Numerator by the Denominator: Divide 16 by 7. This gives us a quotient (the result of the division) and a remainder.
16 ÷ 7 = 2 with a remainder of 2
-
Identify the Whole Number: The quotient (2 in this case) becomes the whole number part of our mixed number.
-
Identify the Fractional Part: The remainder (2 in this case) becomes the numerator of the fractional part. The denominator remains the same as the original fraction (7).
-
Combine the Whole Number and the Fraction: Combine the whole number and the fraction to form the mixed number.
Therefore, 16/7 as a mixed number is 2 ²⁄₇.
Visualizing the Conversion
Imagine you have 16 identical cookies, and you want to share them equally among 7 friends. You can give each friend 2 whole cookies (7 x 2 = 14 cookies). You'll have 2 cookies left over (16 - 14 = 2). These remaining 2 cookies represent the fraction ²⁄₇, representing two out of seven cookies that couldn't be equally distributed. Thus, you have 2 whole sets of cookies and ²⁄₇ of another set, visually representing the mixed number 2 ²⁄₇.
The Mathematical Explanation Behind the Conversion
The conversion from an improper fraction to a mixed number is fundamentally based on the principle of representing a quantity in different forms while maintaining its value. Let's break it down mathematically:
16/7 can be expressed as the sum of its whole number parts and fractional part:
16/7 = (14/7) + (2/7)
Since 14/7 simplifies to 2 (because 14 divided by 7 equals 2), we have:
16/7 = 2 + (2/7) = 2 ²⁄₇
This demonstrates that the process of division is simply separating the whole number components from the fractional component of the improper fraction.
Converting Mixed Numbers Back to Improper Fractions
The reverse process—converting a mixed number back to an improper fraction—is equally important. Let’s use our example of 2 ²⁄₇:
-
Multiply the whole number by the denominator: 2 x 7 = 14
-
Add the numerator: 14 + 2 = 16
-
Keep the denominator the same: The denominator remains 7.
Therefore, the improper fraction equivalent of 2 ²⁄₇ is 16/7. This conversion is essential for various mathematical operations where working with improper fractions is more convenient.
Applications of Mixed Numbers
Mixed numbers are frequently encountered in various real-world applications and mathematical contexts:
-
Measurement: Measuring lengths, weights, or volumes often results in mixed numbers. For example, a piece of wood might measure 3 ⅛ feet long.
-
Cooking and Baking: Recipes often utilize mixed numbers to specify ingredient quantities. A recipe might call for 1 ½ cups of flour.
-
Time: Representing time uses mixed numbers implicitly. For example, 2 hours and 30 minutes is equivalent to 2 ½ hours.
-
Data Analysis and Statistics: Mixed numbers can be used to represent averages or other statistical measures, especially when dealing with quantities that are greater than one whole unit.
-
Fractional Arithmetic: While it's often easier to perform calculations with improper fractions, representing the final answer as a mixed number provides a more intuitive and easily understandable result.
Frequently Asked Questions (FAQ)
Q: Can any improper fraction be converted into a mixed number?
A: Yes, any improper fraction can be converted into a mixed number. The process remains the same: divide the numerator by the denominator, and use the quotient and remainder to construct the mixed number.
Q: What if the remainder is 0 after division?
A: If the remainder is 0, it means the improper fraction is actually a whole number. For example, 14/7 simplifies to 2, as there is no remainder.
Q: Is it always necessary to convert an improper fraction to a mixed number?
A: Not necessarily. Sometimes, leaving the fraction as an improper fraction is more convenient for certain calculations. However, mixed numbers provide a more readily understandable representation of a quantity in many real-world contexts.
Q: Are there any shortcuts for converting improper fractions to mixed numbers?
A: While the standard division method is reliable, with practice, you can develop a mental estimation to quickly convert simpler improper fractions.
Conclusion: Mastering Mixed Numbers
Understanding how to convert improper fractions to mixed numbers, and vice-versa, is a crucial skill in mathematics. This comprehensive guide has provided a detailed explanation of the process, along with visual representations and practical applications. By grasping the fundamental principles behind this conversion, you'll build a strong foundation for tackling more advanced mathematical concepts involving fractions. The ability to confidently work with mixed numbers opens doors to a wider range of mathematical problems and real-world applications, empowering you with greater mathematical fluency. Remember the core principle: it's all about expressing the same quantity in different, equally valid mathematical forms. Through practice and consistent application, you will master this essential skill.
Latest Posts
Latest Posts
-
120 Days From May 1
Sep 19, 2025
-
Convert 62 F To C
Sep 19, 2025
-
600 Square Feet Room Size
Sep 19, 2025
-
10 Out Of 13 Percent
Sep 19, 2025
-
14 16 As A Percent
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 16/7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.