17 25 As A Decimal
saludintensiva
Sep 18, 2025 · 5 min read
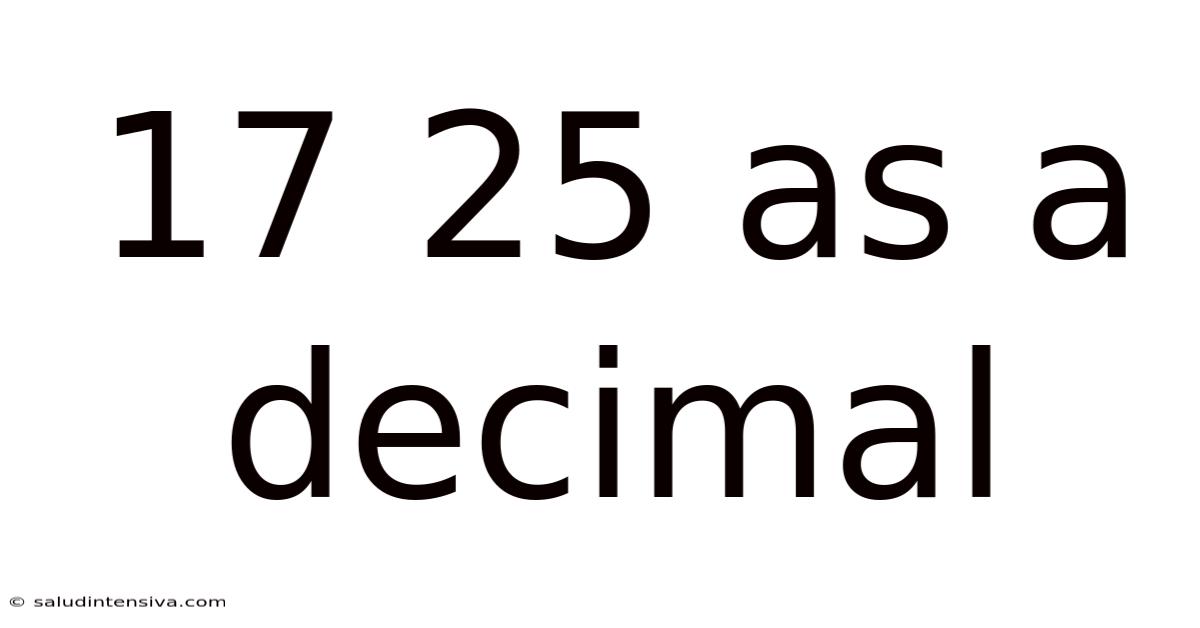
Table of Contents
17/25 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article provides a comprehensive guide to converting the fraction 17/25 into its decimal form, exploring various methods and delving into the underlying principles. We'll cover not just the how but also the why, ensuring you gain a deeper understanding of this essential mathematical concept. This guide is perfect for students, educators, and anyone looking to solidify their knowledge of fraction-to-decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 17/25, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals use a decimal point (.) to separate the whole number part from the fractional part. For example, 0.5 is equivalent to 5/10, and 0.25 is equivalent to 25/100.
The ability to convert between fractions and decimals is crucial for various applications in mathematics, science, and everyday life.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. To convert 17/25 to a decimal, we simply divide the numerator (17) by the denominator (25):
17 ÷ 25 = 0.68
Therefore, 17/25 as a decimal is 0.68. This method is readily applicable using a calculator or by performing long division manually. Long division provides a deeper understanding of the process, illustrating how the fraction is broken down into smaller parts.
Method 2: Equivalent Fractions
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10. This makes it easy to express the fraction as a decimal. While 25 isn't directly a power of 10, we can find an equivalent fraction by multiplying both the numerator and denominator by a suitable number.
Since 25 multiplied by 4 equals 100, we can multiply both the numerator and the denominator of 17/25 by 4:
(17 x 4) / (25 x 4) = 68/100
Now, 68/100 can be easily expressed as a decimal:
68/100 = 0.68
This method highlights the concept of equivalent fractions and demonstrates that multiplying or dividing both the numerator and denominator by the same non-zero number doesn't change the value of the fraction. It's a valuable technique for converting fractions with denominators that are factors of powers of 10.
Method 3: Understanding Place Value
Let's look at the decimal 0.68 and break down its place value. The digit 6 is in the tenths place, representing 6/10. The digit 8 is in the hundredths place, representing 8/100. Therefore, 0.68 can be written as:
6/10 + 8/100 = 60/100 + 8/100 = 68/100
This reinforces the understanding of how decimals represent fractions with denominators that are powers of 10. It provides a deeper comprehension of the relationship between the decimal representation and the fractional form.
The Importance of Decimal Representation
The conversion of fractions to decimals is essential for several reasons:
-
Simplification of Calculations: Decimals are often easier to work with in calculations, particularly when using calculators or computers. Adding, subtracting, multiplying, and dividing decimals is generally more straightforward than performing the same operations with fractions.
-
Comparison and Ordering: Comparing the size of fractions can be challenging. Converting them to decimals allows for easier comparison and ordering. For example, determining which is larger, 17/25 or 1/2, is easier after converting them to decimals (0.68 and 0.5 respectively).
-
Real-World Applications: Decimals are widely used in various real-world applications, including finance, engineering, science, and everyday measurements. Understanding decimal representation is critical for interpreting data and performing calculations in these fields.
Frequently Asked Questions (FAQ)
Q1: Are there other methods to convert 17/25 to a decimal?
A1: While the methods described above are the most common and efficient, you could also use a combination of techniques, such as simplifying the fraction before converting to a decimal or using a different equivalent fraction. However, the direct division and equivalent fraction methods remain the most straightforward.
Q2: Can all fractions be converted to terminating decimals?
A2: No, not all fractions can be converted to terminating decimals. Fractions with denominators that have prime factors other than 2 and 5 (when expressed in their simplest form) will result in repeating or recurring decimals. For example, 1/3 converts to 0.333... (a recurring decimal). 17/25, however, converts to a terminating decimal because its denominator, 25, is 5².
Q3: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A3: Improper fractions will convert to decimals greater than 1. The process of conversion remains the same: divide the numerator by the denominator. For instance, 25/10 would convert to 2.5.
Q4: How can I improve my skills in fraction-to-decimal conversions?
A4: Practice is key! Work through various examples, starting with simple fractions and gradually progressing to more complex ones. Use different methods to solve the same problem to reinforce your understanding. Understand the underlying principles of place value and equivalent fractions. Regular practice will build your confidence and proficiency.
Conclusion
Converting 17/25 to a decimal is a straightforward process that can be accomplished using various methods, including direct division and the equivalent fraction method. Understanding these methods, alongside the underlying principles of fractions and decimals, is crucial for developing a strong foundation in mathematics. The ability to seamlessly convert between fractions and decimals is a vital skill applicable across many areas of study and daily life. Remember that while calculators offer a quick solution, understanding the why behind the conversion is equally important for true mathematical comprehension. This will not only help you solve problems effectively but also foster a deeper appreciation for the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Absolute Value Of And 8
Sep 18, 2025
-
What Is Equal To 4 5
Sep 18, 2025
-
Standard Form And Expanded Form
Sep 18, 2025
-
How Do You Calculate Capacity
Sep 18, 2025
-
3 Feet By 4 Feet
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 17 25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.