17 25 As A Percent
saludintensiva
Sep 14, 2025 · 5 min read
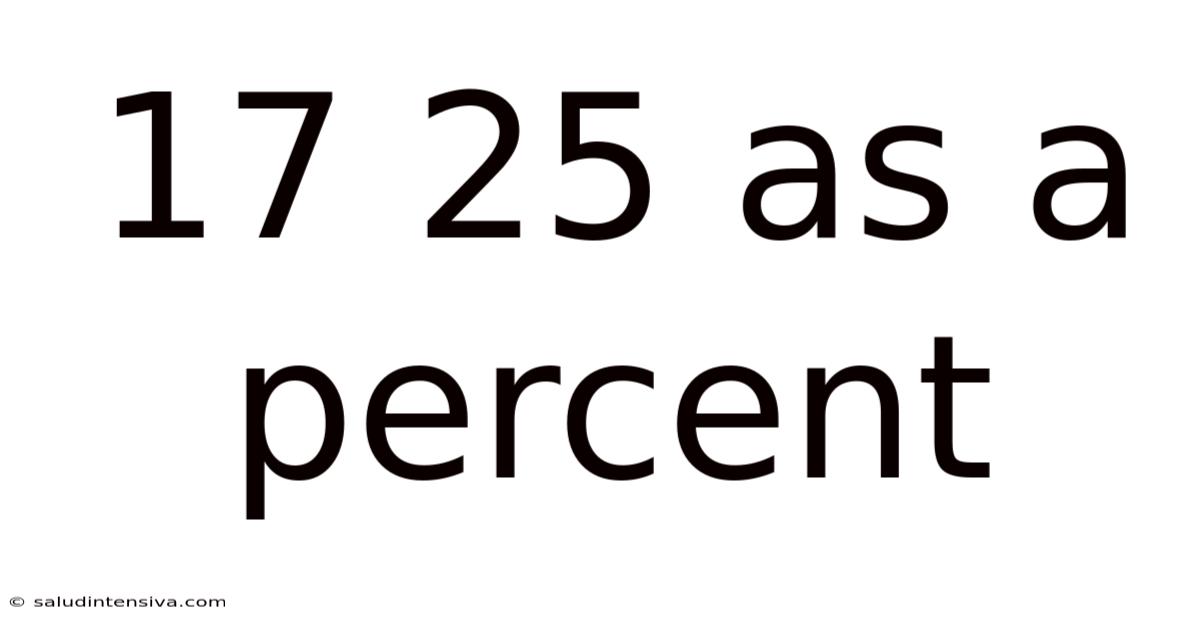
Table of Contents
17/25 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This comprehensive guide will delve into the process of converting fractions to percentages, focusing specifically on how to express 17/25 as a percentage. We’ll cover the calculation steps, explore the underlying mathematical principles, and even touch upon real-world applications. By the end, you’ll not only know the answer but also understand the method well enough to tackle similar problems independently.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred." Therefore, when we say "x percent," we are stating that x out of every 100 units represents that proportion. Converting fractions to percentages involves finding the equivalent fraction with a denominator of 100, or equivalently, multiplying the fraction by 100%. This is a crucial concept in numerous fields, including:
- Finance: Calculating interest rates, discounts, and profit margins.
- Statistics: Representing data proportions and probabilities.
- Science: Expressing experimental results and error margins.
- Everyday Life: Calculating tips, sales tax, and understanding discounts.
Calculating 17/25 as a Percentage: A Step-by-Step Guide
Let's break down how to convert the fraction 17/25 into a percentage. There are two primary methods:
Method 1: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding a number that, when multiplied by the denominator (25), results in 100. In this case, that number is 4 (since 25 x 4 = 100). Because we multiply the denominator by 4, we must also multiply the numerator by 4 to maintain the equivalence of the fraction:
17/25 = (17 x 4) / (25 x 4) = 68/100
Since 68/100 means 68 out of every 100, this fraction is equivalent to 68%.
Method 2: Using the Percentage Formula
The general formula for converting a fraction to a percentage is:
(Numerator / Denominator) x 100%
Applying this formula to our fraction 17/25:
(17 / 25) x 100% = 0.68 x 100% = 68%
Both methods yield the same result: 17/25 is equal to 68%.
Understanding the Mathematical Principles
The core concept behind percentage calculations lies in the relationship between fractions, decimals, and percentages. They are all different ways of representing the same proportion.
- Fractions: Express a part as a ratio of a whole (e.g., 17/25).
- Decimals: Express a part as a value between 0 and 1 (e.g., 0.68).
- Percentages: Express a part as a fraction of 100 (e.g., 68%).
Converting between these forms involves simple arithmetic operations:
- Fraction to Decimal: Divide the numerator by the denominator (17 ÷ 25 = 0.68).
- Decimal to Percentage: Multiply the decimal by 100% (0.68 x 100% = 68%).
- Percentage to Decimal: Divide the percentage by 100% (68% ÷ 100% = 0.68).
- Decimal to Fraction: Express the decimal as a fraction with a denominator of a power of 10 (0.68 = 68/100, which simplifies to 17/25).
Real-World Applications of Percentage Calculations: Beyond 17/25
The ability to convert fractions to percentages is crucial in many real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $50, the discount amount is (20/100) x $50 = $10. The final price would be $50 - $10 = $40.
-
Determining Grades: If a student scores 17 out of 25 on a test, their percentage score is 68%, indicating a good performance.
-
Analyzing Financial Statements: Companies use percentages to represent profit margins, growth rates, and other key financial metrics. For instance, if a company's revenue increased by $17 million out of a total revenue of $25 million, their revenue growth is 68%.
-
Understanding Statistics: Percentages are frequently used to present survey results, population statistics, and various other data sets. For example, if 17 out of 25 people surveyed prefer a particular brand, then 68% prefer that brand.
-
Calculating Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. For instance, a 6% sales tax on a $100 purchase would be (6/100) x $100 = $6.
These examples showcase the versatility and importance of understanding percentage calculations in various contexts.
Frequently Asked Questions (FAQ)
Q: What if the denominator isn't easily divisible to get 100?
A: If the denominator doesn't easily convert to 100, simply use the formula (Numerator / Denominator) x 100%. This works for any fraction.
Q: Can I use a calculator for percentage calculations?
A: Yes, absolutely! Calculators are incredibly helpful for percentage calculations, especially when dealing with more complex fractions or decimals.
Q: What if I have a percentage and need to find the equivalent fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 68% becomes 68/100, which simplifies to 17/25.
Q: Are there any online tools or resources to help with percentage calculations?
A: Numerous websites and apps offer percentage calculators that can assist with converting fractions and decimals to percentages and vice-versa. These tools can be very useful for checking your work or for solving more complex problems.
Conclusion: Mastering Percentage Calculations
The ability to convert fractions to percentages is a fundamental mathematical skill with broad applications. Understanding the process, whether through finding an equivalent fraction with a denominator of 100 or using the percentage formula, is key. The example of converting 17/25 to 68% illustrates a simple yet important concept that forms the basis of many more complex calculations. By mastering this skill, you’ll gain a valuable tool applicable in various academic, professional, and everyday situations. Remember to practice regularly to build your proficiency and confidence. From calculating discounts to understanding statistical data, a firm grasp of percentages opens up a world of possibilities. With consistent practice and a clear understanding of the principles involved, you'll find yourself confidently tackling percentage-related problems in any context.
Latest Posts
Latest Posts
-
25 Out Of 30 Percentage
Sep 14, 2025
-
Gcf Of 56 And 35
Sep 14, 2025
-
30 Days From October 22nd
Sep 14, 2025
-
Alphabet Letter To Number Converter
Sep 14, 2025
-
Section Is How Many Acres
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 17 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.