19 50 As A Decimal
saludintensiva
Sep 13, 2025 · 5 min read
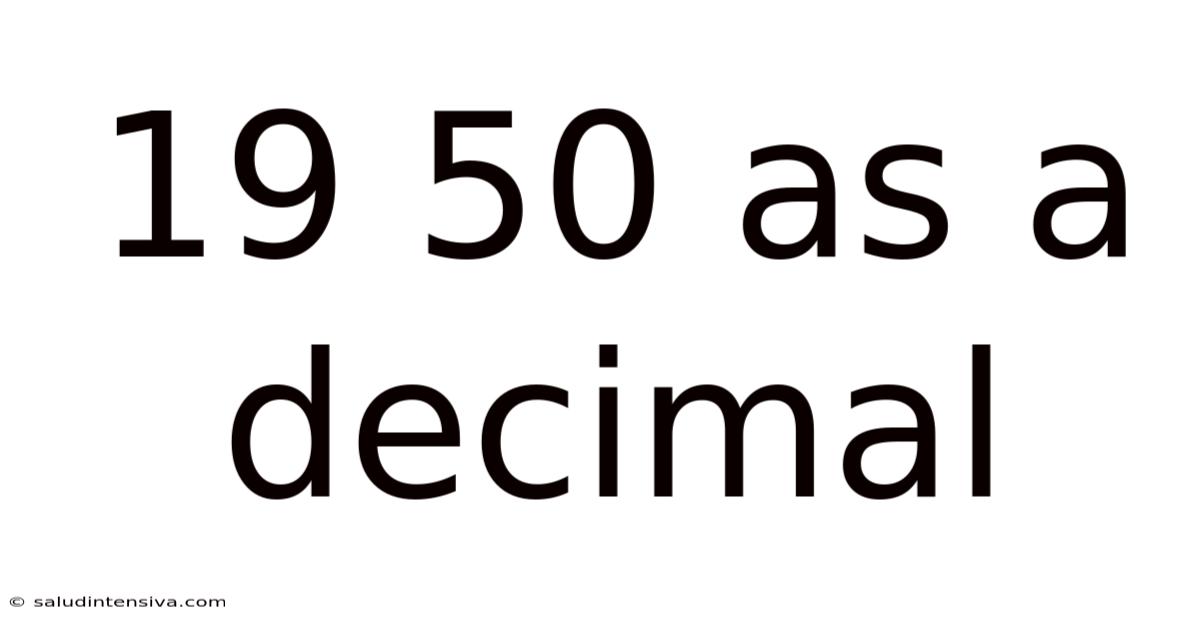
Table of Contents
19/50 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, applicable across various fields from basic arithmetic to advanced calculus. This comprehensive guide will walk you through the process of converting the fraction 19/50 to its decimal equivalent, explaining the underlying principles and providing additional context to solidify your understanding. We'll also explore different methods for achieving this conversion, addressing common misconceptions and frequently asked questions.
Understanding Fractions and Decimals
Before diving into the specific conversion of 19/50, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
A decimal, on the other hand, represents a number based on powers of ten. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Converting a fraction to a decimal essentially means expressing the fractional part of a whole as a decimal representation.
Method 1: Direct Division
The most straightforward method for converting a fraction to a decimal is through direct division. To convert 19/50 to a decimal, we simply divide the numerator (19) by the denominator (50):
19 ÷ 50 = 0.38
Therefore, 19/50 as a decimal is 0.38. This method is easily performed using a calculator or even manually using long division.
Method 2: Equivalent Fractions with a Denominator of 10, 100, 1000, etc.
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This method is particularly useful when the denominator has factors that can be easily multiplied to reach a power of 10.
In the case of 19/50, we can observe that 50 can be easily converted to 100 by multiplying by 2:
50 x 2 = 100
To maintain the equivalence of the fraction, we must also multiply the numerator by 2:
19 x 2 = 38
This gives us the equivalent fraction 38/100. Since 1/100 is equal to 0.01, 38/100 can be directly written as a decimal:
38/100 = 0.38
This method elegantly demonstrates the relationship between fractions and decimals, highlighting how different representations can express the same value.
Understanding the Decimal Place Value
The result, 0.38, represents 3 tenths and 8 hundredths. Understanding decimal place value is crucial in interpreting decimal numbers accurately. Each digit to the right of the decimal point represents a progressively smaller fraction of a whole:
- 0.1 (one tenth)
- 0.01 (one hundredth)
- 0.001 (one thousandth)
- and so on…
In 0.38, the '3' in the tenths place signifies 3/10, and the '8' in the hundredths place signifies 8/100. Adding these together, we get (3/10) + (8/100) = 38/100, which is equivalent to 19/50.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals has wide-ranging practical applications:
-
Financial Calculations: Dealing with percentages, interest rates, and monetary values often requires converting fractions to decimals. For instance, calculating discounts or understanding interest accrual frequently involves decimal representations.
-
Scientific Measurements: In scientific fields, precise measurements are crucial, and decimals are frequently used to express values more accurately than fractions. The precision offered by decimals is often essential in various scientific calculations.
-
Engineering and Design: In engineering and design, decimal numbers are extensively used for precise calculations and measurements, ensuring the accuracy needed for building structures, machines, and other constructs.
-
Everyday Calculations: Converting fractions to decimals can simplify calculations in daily life, like splitting bills, calculating tips, or measuring ingredients in cooking.
Common Misconceptions and Pitfalls
While converting fractions to decimals seems straightforward, certain misconceptions can lead to errors:
-
Incorrect Placement of the Decimal Point: Careless calculation can lead to the decimal point being placed incorrectly, resulting in a significant error in the value.
-
Confusion with Percentages: While closely related, decimals and percentages are not interchangeable. A decimal needs to be multiplied by 100 to convert it to a percentage. For instance, 0.38 is equivalent to 38%.
-
Rounding Errors: When dealing with repeating decimals, rounding off to a certain number of decimal places might introduce a slight inaccuracy.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that are not factors of powers of 10 (i.e., they contain prime factors other than 2 and 5) will result in repeating decimals (e.g., 1/3 = 0.333...).
Q: What is the difference between a terminating and a repeating decimal?
A: A terminating decimal has a finite number of digits after the decimal point, while a repeating decimal has a sequence of digits that repeat infinitely.
Q: How can I convert a mixed number (a whole number and a fraction) to a decimal?
A: First, convert the fraction part to a decimal using the methods described above. Then, add the whole number to the resulting decimal.
Q: Are there any online tools or calculators to help with fraction to decimal conversions?
A: Yes, many online calculators and conversion tools are available to assist with this. However, understanding the underlying principles is essential for building a strong mathematical foundation.
Conclusion
Converting 19/50 to a decimal is a relatively simple process, achievable through direct division or by finding an equivalent fraction with a denominator of 100. Understanding the underlying principles of fractions, decimals, and place value is crucial for accurate conversion and application in various contexts. This guide aims not just to provide the answer (0.38) but to equip you with the knowledge and understanding to tackle similar conversions confidently and efficiently. Mastering this fundamental skill lays the groundwork for success in more advanced mathematical concepts. Remember to practice regularly to solidify your understanding and improve your speed and accuracy in performing these essential calculations.
Latest Posts
Latest Posts
-
3 4 As An Improper Fraction
Sep 14, 2025
-
Generate 6 Digit Random Number
Sep 14, 2025
-
300 Meters Converted To Feet
Sep 14, 2025
-
Whats 10 As A Fraction
Sep 14, 2025
-
Greatest Common Factor Of 13
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 19 50 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.