2 1 3 In Decimal
saludintensiva
Sep 14, 2025 · 5 min read
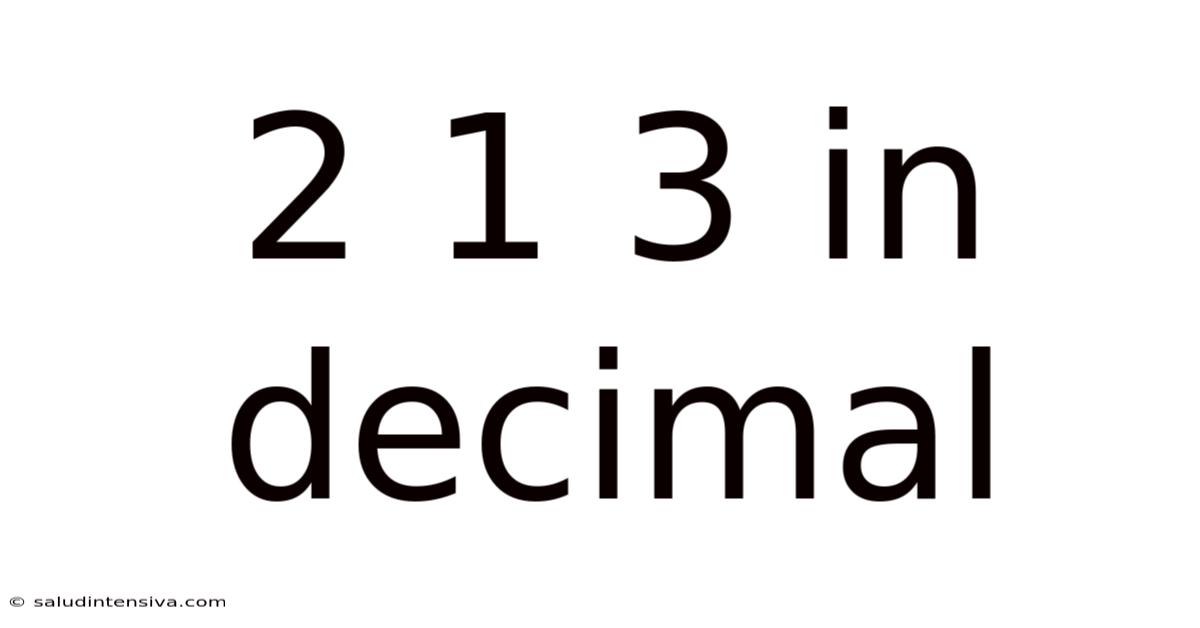
Table of Contents
Understanding the Decimal Representation of 2 1 3: A Deep Dive
The seemingly simple notation "2 1 3" can be quite misleading. It's not immediately clear what this represents: is it a single number, a sequence of numbers, a code, or something else entirely? This article will explore the various interpretations of "2 1 3" in the context of decimal representation, delving into its potential meanings, mathematical implications, and the underlying principles of base-10 systems. We'll also address common misconceptions and provide a comprehensive understanding suitable for individuals with varying levels of mathematical background.
What is a Decimal Number System?
Before we dissect "2 1 3", it's crucial to understand the foundation: the decimal (or base-10) number system. This is the system we use every day. It's characterized by the use of ten digits – 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 – to represent any number. The position of each digit determines its value; moving left from the decimal point (.), each position represents a successively higher power of 10.
For example, the number 1234 is interpreted as:
- 1 * 10³ (one thousand)
- 2 * 10² (two hundred)
- 3 * 10¹ (thirty)
- 4 * 10⁰ (four)
The sum of these values (1000 + 200 + 30 + 4) equals 1234. This positional notation is the cornerstone of our understanding of decimal numbers.
Interpreting "2 1 3": Potential Meanings
The ambiguity of "2 1 3" arises from the lack of clear separators or contextual information. It could represent several things:
1. A Sequence of Three Separate Numbers: The simplest interpretation is that "2 1 3" represents three distinct integers: 2, 1, and 3. This is a straightforward reading, but it doesn't leverage the inherent structure of a decimal number system. In a programming context, this could be a simple array or list.
2. A Single Three-Digit Number: If we assume "2 1 3" represents a single decimal number, we have a three-digit integer with the digits 2, 1, and 3 in the hundreds, tens, and units places respectively. This would be the decimal representation of two hundred and thirteen (213). This is the most likely interpretation if no further context is provided.
3. A Representation in a Non-Decimal Base: While less likely without further information, "2 1 3" could potentially represent a number in a different base (like base-4, base-5, or another non-decimal system). However, this interpretation requires additional context specifying the base being used. For example, if the base were 4, the number "213" in base 4 would be:
- (2 * 4²) + (1 * 4¹) + (3 * 4⁰) = 32 + 4 + 3 = 39 in decimal.
4. A Code or Symbolic Representation: In certain contexts, "2 1 3" could represent a code, a symbol, or an abbreviation unrelated to numerical values. Without knowing the specific system or convention, it's impossible to decipher its meaning. This is entirely dependent on context.
Mathematical Operations with 213 (Assuming Decimal Interpretation)
If we assume "2 1 3" refers to the decimal number 213, we can perform various mathematical operations:
- Addition: 213 + 100 = 313; 213 + 213 = 426
- Subtraction: 213 - 100 = 113; 213 - 50 = 163
- Multiplication: 213 * 2 = 426; 213 * 10 = 2130
- Division: 213 / 3 = 71; 213 / 10 = 21.3
- Prime Factorization: 213 = 3 x 71 (both 3 and 71 are prime numbers). Understanding prime factorization is fundamental in number theory and cryptography.
- Modular Arithmetic: 213 mod 10 = 3 (the remainder when 213 is divided by 10). Modular arithmetic has applications in cryptography and computer science.
Exploring the Decimal System Further: Place Value and Significant Digits
Understanding place value is essential when working with decimal numbers. Each position in a decimal number represents a power of 10. For example, in the number 213:
- The digit 2 is in the hundreds place (10²), representing 200.
- The digit 1 is in the tens place (10¹), representing 10.
- The digit 3 is in the units place (10⁰), representing 3.
The concept of significant digits also plays a crucial role. Significant digits are the digits in a number that carry meaning contributing to its precision. In the number 213, all three digits are significant. However, in a number like 0.00213, only the digits 2, 1, and 3 are significant; the leading zeros are placeholders.
Common Misconceptions about Decimal Numbers
Several common misconceptions surround decimal numbers:
- Decimal Point Confusion: Many struggle with the placement and interpretation of the decimal point. Remember that the decimal point separates the whole number part from the fractional part.
- Rounding Errors: Rounding off numbers can introduce errors, especially in calculations involving many steps.
- Scientific Notation: Scientific notation (e.g., 2.13 x 10²) is often misunderstood. It provides a concise way to represent very large or very small numbers.
Frequently Asked Questions (FAQ)
Q: What is the largest three-digit number in the decimal system?
A: 999
Q: How do you convert a fraction to a decimal?
A: Divide the numerator by the denominator. For example, 1/4 = 0.25
Q: What is the difference between a decimal and a fraction?
A: Both represent parts of a whole, but decimals use a base-10 system with a decimal point, while fractions represent a ratio of two integers.
Q: Can a decimal number be negative?
A: Yes, decimal numbers can be negative (e.g., -213).
Conclusion: The Importance of Context and Precision
The interpretation of "2 1 3" highlights the importance of context and clear communication in mathematics. While it most likely represents the decimal number 213, its meaning can shift depending on the situation. Understanding the fundamental principles of the decimal number system, including place value, significant digits, and different number representations, is essential for effective mathematical work and clear communication. This detailed exploration should solidify your understanding of decimal representation and its implications. The seemingly simple "2 1 3" opens the door to deeper mathematical concepts, demonstrating the rich possibilities embedded within a basic number system. Remember, precision and clear communication are key to avoid ambiguity in any mathematical context.
Latest Posts
Latest Posts
-
Lcm Of 3 8 6
Sep 14, 2025
-
4800 Square Feet To Acres
Sep 14, 2025
-
60 Days From May 30
Sep 14, 2025
-
Nevada Total Sales Tax Rate
Sep 14, 2025
-
999 Into Hours And Minutes
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 1 3 In Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.