2 3/4 Divided By 3
saludintensiva
Sep 14, 2025 · 6 min read
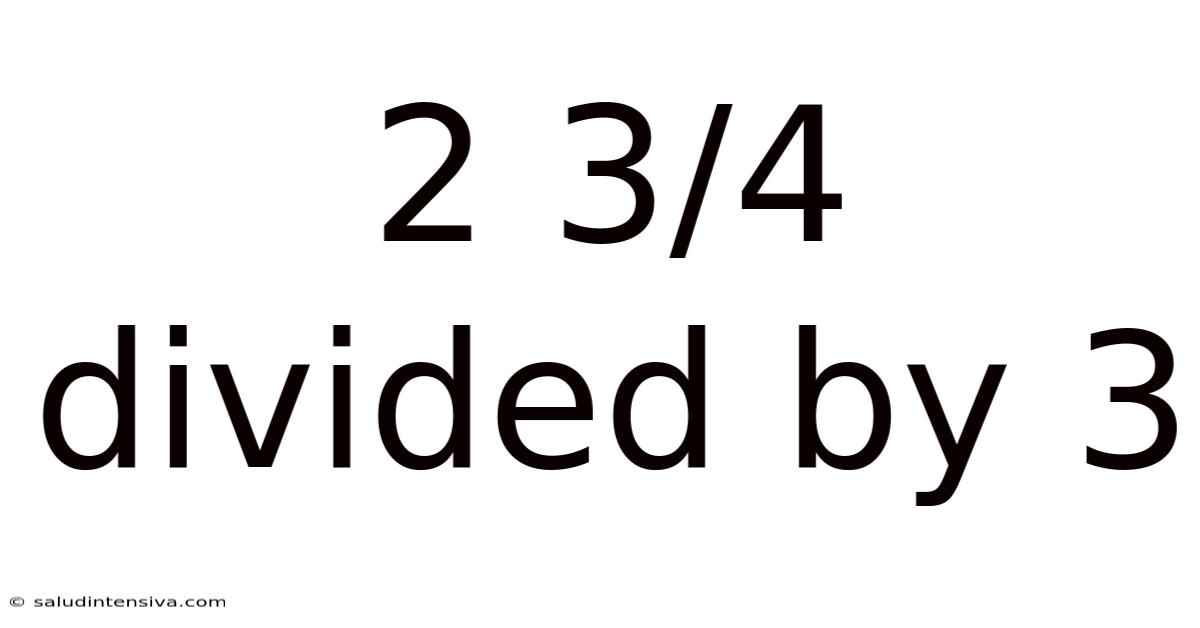
Table of Contents
Diving Deep into 2 3/4 Divided by 3: A Comprehensive Guide
Dividing fractions and mixed numbers can seem daunting, but with a structured approach, it becomes manageable and even enjoyable! This article will guide you through solving 2 3/4 divided by 3, explaining the process step-by-step, providing the scientific rationale behind the method, and answering frequently asked questions. Understanding this seemingly simple calculation unlocks a deeper understanding of fractional arithmetic, crucial for various mathematical applications. We’ll explore different methods, ensuring you grasp the core concepts and can confidently tackle similar problems in the future.
Understanding the Problem: 2 3/4 ÷ 3
Before we dive into the solution, let's break down the problem: 2 3/4 ÷ 3. This represents the task of dividing the mixed number 2 3/4 into three equal parts. Imagine you have 2 ¾ pizzas and you want to share them equally among 3 people. How much pizza does each person get? This real-world analogy helps visualize the mathematical operation. The keyword here is "division" – splitting something into equal parts.
Method 1: Converting to Improper Fractions
This is the most common and generally preferred method for dividing mixed numbers. It involves transforming the mixed number into an improper fraction before performing the division.
Step 1: Convert the Mixed Number to an Improper Fraction
A mixed number combines a whole number and a fraction (e.g., 2 3/4). To convert it to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 2 x 4 = 8
- Add the numerator: 8 + 3 = 11
- Keep the same denominator: 4
Therefore, 2 3/4 becomes 11/4.
Step 2: Rewrite the Division Problem
Our problem now becomes: 11/4 ÷ 3
Step 3: Convert the Whole Number to a Fraction
To divide fractions, it's easiest to work with fractions only. We can represent the whole number 3 as a fraction: 3/1.
Step 4: Invert the Second Fraction and Multiply
Dividing by a fraction is the same as multiplying by its reciprocal (the fraction flipped upside down). The reciprocal of 3/1 is 1/3. So our problem becomes:
11/4 x 1/3
Step 5: Multiply the Numerators and Denominators
Multiply the numerators (top numbers) together: 11 x 1 = 11 Multiply the denominators (bottom numbers) together: 4 x 3 = 12
This gives us the improper fraction: 11/12
Step 6: Simplify (if necessary)
In this case, 11/12 is already in its simplest form because 11 and 12 have no common factors other than 1.
Therefore, 2 3/4 divided by 3 is 11/12.
Method 2: Using Decimal Representation
An alternative method involves converting both the mixed number and the whole number into their decimal equivalents. While this method might seem simpler initially, it can sometimes lead to rounding errors, especially with more complex fractions.
Step 1: Convert the Mixed Number to a Decimal
To convert 2 3/4 to a decimal, we can first convert the fraction 3/4 to a decimal: 3 ÷ 4 = 0.75. Then add the whole number: 2 + 0.75 = 2.75
Step 2: Perform the Division
Now, we divide the decimal representation: 2.75 ÷ 3 = 0.916666...
Step 3: Round (if necessary)
The result is a repeating decimal. Depending on the required level of precision, you might round this to a specific number of decimal places. For instance, rounding to two decimal places gives 0.92.
Comparing the Two Methods
Both methods yield the same result, albeit in different forms. Method 1 (converting to improper fractions) provides a precise, non-rounded answer (11/12), while Method 2 (using decimals) can introduce rounding errors depending on how many decimal places you retain. For accuracy and avoiding approximation, the improper fraction method is generally preferred, especially when working with further calculations.
The Scientific Rationale: Understanding Division of Fractions
The process of dividing fractions hinges on the fundamental concept of reciprocals and the commutative property of multiplication. When we divide by a fraction, we are essentially asking "how many times does this fraction fit into the other?" Inverting and multiplying achieves this by effectively scaling the problem.
Let's consider a simpler example: 1/2 ÷ 1/4. This asks how many 1/4s are in 1/2? Visually, two 1/4s make up 1/2. Mathematically, we get:
1/2 ÷ 1/4 = 1/2 x 4/1 = 4/2 = 2
The act of inverting the second fraction and multiplying effectively scales the problem to find the number of times the divisor (1/4) fits into the dividend (1/2).
Practical Applications: Where This Knowledge is Useful
Understanding division of fractions and mixed numbers extends far beyond the classroom. It's vital in:
- Baking and Cooking: Scaling recipes up or down requires manipulating fractions and mixed numbers.
- Sewing and Crafts: Calculating fabric requirements or dividing materials accurately.
- Construction and Engineering: Precise measurements and calculations in blueprints and designs.
- Data Analysis: Working with proportions and ratios frequently involves fractional arithmetic.
- Finance: Calculating interest rates, proportions of investments, and sharing profits or expenses.
Frequently Asked Questions (FAQs)
Q: Can I divide 2 3/4 by 3 using a calculator?
A: Yes, most calculators can handle fraction division. However, be aware that some calculators might give you a decimal approximation rather than a fractional answer. It’s crucial to understand the underlying mathematical principles regardless of the tools you use.
Q: What if I have a more complex mixed number or divisor?
A: The method of converting to improper fractions and then inverting and multiplying remains the same, no matter the complexity of the numbers involved. Just be meticulous with your calculations.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the answer easier to understand and interpret. It also provides a more concise and efficient representation of the solution.
Q: What if the result is an improper fraction?
A: An improper fraction (where the numerator is larger than the denominator) simply means the result is greater than one whole. You can convert it back to a mixed number if needed by dividing the numerator by the denominator. For example, 11/12 is already a proper fraction (numerator < denominator).
Conclusion: Mastering Fraction Division
Mastering fraction division, including working with mixed numbers, is a fundamental skill in mathematics. This article has demonstrated two methods for solving 2 3/4 ÷ 3, explained the underlying mathematical principles, and explored practical applications. By understanding the steps involved and the rationale behind them, you'll build confidence in tackling increasingly complex problems. Remember, practice is key to solidifying your understanding and building fluency. Don't be afraid to work through similar problems to reinforce your skills. The more you practice, the easier it will become. So, grab your pencil and paper, and continue exploring the fascinating world of fractions!
Latest Posts
Latest Posts
-
Variance Of A Dice Roll
Sep 14, 2025
-
Lcd Of Rational Expressions Calculator
Sep 14, 2025
-
16 Percent In Decimal Form
Sep 14, 2025
-
What Is 4 1 Simplified
Sep 14, 2025
-
Area Of A Hollow Pipe
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 3/4 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.