2 3 Divided By 15
saludintensiva
Sep 19, 2025 · 5 min read
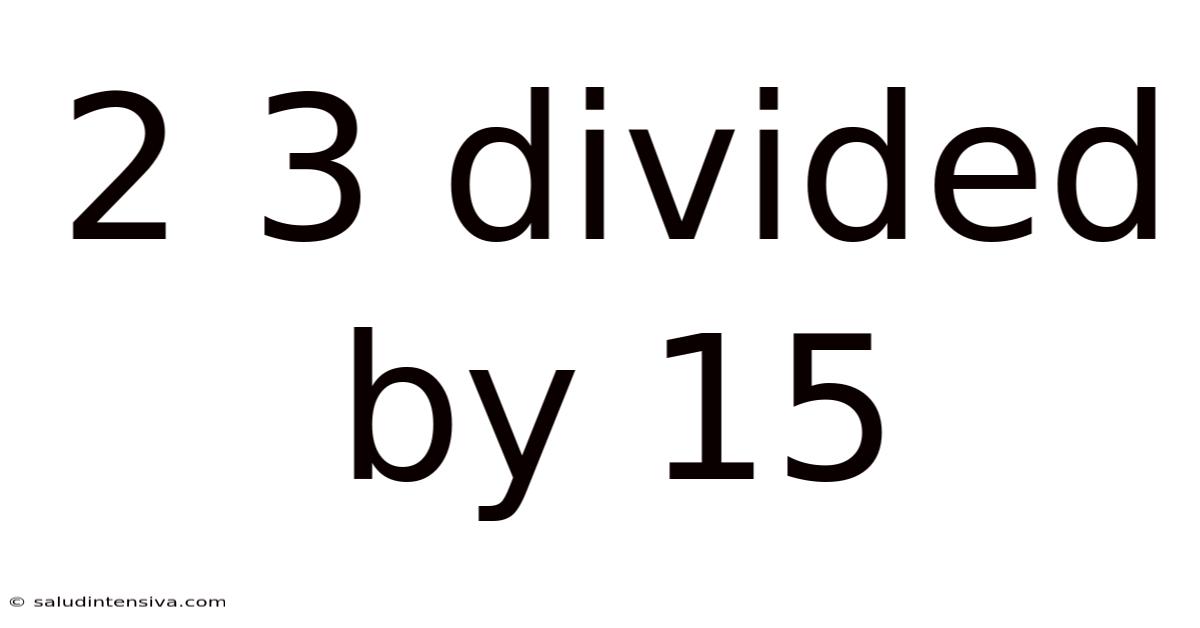
Table of Contents
Decoding 2/3 Divided by 15: A Deep Dive into Fraction Division
Understanding fraction division can seem daunting at first, but with a clear approach and a little practice, it becomes straightforward. This comprehensive guide will break down the process of solving 2/3 divided by 15, explaining not only the steps involved but also the underlying mathematical principles. We'll explore various methods, providing a solid foundation for tackling similar problems in the future. By the end, you’ll not only know the answer but also understand why the answer is what it is.
Understanding the Problem: 2/3 ÷ 15
The problem, "2/3 divided by 15," asks us to determine how many times 15 goes into 2/3. This might seem counterintuitive since 15 is a much larger number than 2/3. However, remember that dividing by a number is the same as multiplying by its reciprocal. This is a crucial concept in fraction division.
Method 1: The Reciprocal Method
This is the most common and efficient method for dividing fractions. The key lies in understanding the reciprocal. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 5 is 1/5, and the reciprocal of 1/2 is 2.
-
Step 1: Express the Whole Number as a Fraction: We can write 15 as a fraction: 15/1.
-
Step 2: Find the Reciprocal of the Divisor: The divisor is 15/1. Its reciprocal is 1/15.
-
Step 3: Change Division to Multiplication: Instead of dividing by 15/1, we'll multiply by its reciprocal, 1/15. Our problem now becomes: (2/3) x (1/15).
-
Step 4: Multiply the Numerators and Denominators: Multiply the numerators (top numbers) together: 2 x 1 = 2. Multiply the denominators (bottom numbers) together: 3 x 15 = 45.
-
Step 5: Simplify the Result: Our result is 2/45. This fraction is already in its simplest form because 2 and 45 share no common factors other than 1.
Therefore, 2/3 divided by 15 equals 2/45.
Method 2: The Common Denominator Method
This method is less commonly used for dividing fractions, but it’s a valuable approach for understanding the underlying concept. It involves converting both the fraction and the whole number into fractions with a common denominator.
-
Step 1: Express the Whole Number as a Fraction: Again, we write 15 as 15/1.
-
Step 2: Find a Common Denominator: The denominator of our fraction 2/3 is 3. To find a common denominator with 15/1, we need to find a number that both 3 and 1 can divide into. The least common multiple of 3 and 1 is 3.
-
Step 3: Rewrite the Fractions with the Common Denominator: 2/3 stays as it is. 15/1 becomes 45/3 (because we multiplied both the numerator and denominator by 3).
-
Step 4: Divide the Numerators: Now we can divide the numerators: 2 ÷ 45. This is equivalent to 2/45.
-
Step 5: Simplify the Result: As before, the result is already simplified as 2/45.
Method 3: Visual Representation
While less practical for complex calculations, a visual approach can help solidify your understanding. Imagine a pizza cut into three slices. You have two of those slices (2/3 of the pizza). Now you want to divide these two slices among 15 people. Each person would receive a very small portion of the pizza. That small portion represents 2/45 of the whole pizza.
Explanation of the Result: 2/45
The result, 2/45, signifies that if you divide 2/3 into 15 equal parts, each part will be 2/45 of the original whole. This small fraction highlights that dividing a fraction by a larger whole number results in a smaller fraction.
Why the Reciprocal Method Works
The reason the reciprocal method works boils down to the definition of division. Division is the inverse operation of multiplication. When we divide by a fraction, we are essentially asking, "What number, when multiplied by the divisor, gives us the dividend?" Using the reciprocal allows us to turn the division problem into a multiplication problem, which is generally easier to solve.
Practical Applications
Understanding fraction division has countless real-world applications:
- Baking: Dividing ingredients in recipes often requires fraction division.
- Sewing: Calculating fabric amounts often involves fractions and division.
- Construction: Precise measurements in construction projects often involve fractional calculations.
- Engineering: Designing and building structures often relies on precise fraction division.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this?
- A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving and to avoid dependence on technology.
-
Q: What if the fraction was larger than the whole number?
- A: If the fraction were larger than the whole number (e.g., 5/2 ÷ 2), the result would be a fraction greater than 1 (in this case, 5/4 or 1 1/4).
-
Q: What if I get a mixed number as a result?
- A: A mixed number is a combination of a whole number and a fraction. You can convert it into an improper fraction (where the numerator is larger than the denominator) for easier calculations or leave it as a mixed number.
-
Q: Are there other ways to simplify the fraction 2/45?
- A: No. 2 and 45 have no common factors other than 1, meaning the fraction is already in its simplest form.
Conclusion
Dividing fractions can appear complex initially, but by understanding the concepts of reciprocals and common denominators, the process becomes manageable. This article has explored multiple approaches to solving 2/3 divided by 15, highlighting that the answer is 2/45. Remember, mastering fraction division is a valuable skill with far-reaching applications in various fields. By practicing different methods and applying your knowledge to real-world scenarios, you'll build confidence and proficiency in this essential mathematical skill. Don't be afraid to tackle more complex fraction division problems; with consistent practice, you'll find them increasingly straightforward.
Latest Posts
Latest Posts
-
12 16 In Lowest Terms
Sep 19, 2025
-
18 25 As A Percentage
Sep 19, 2025
-
Home Depreciation Calculator For Taxes
Sep 19, 2025
-
How To Calculate Pixel Size
Sep 19, 2025
-
13 3 As A Mixed Number
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Divided By 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.