2 3 Of 1 3
saludintensiva
Sep 13, 2025 · 5 min read
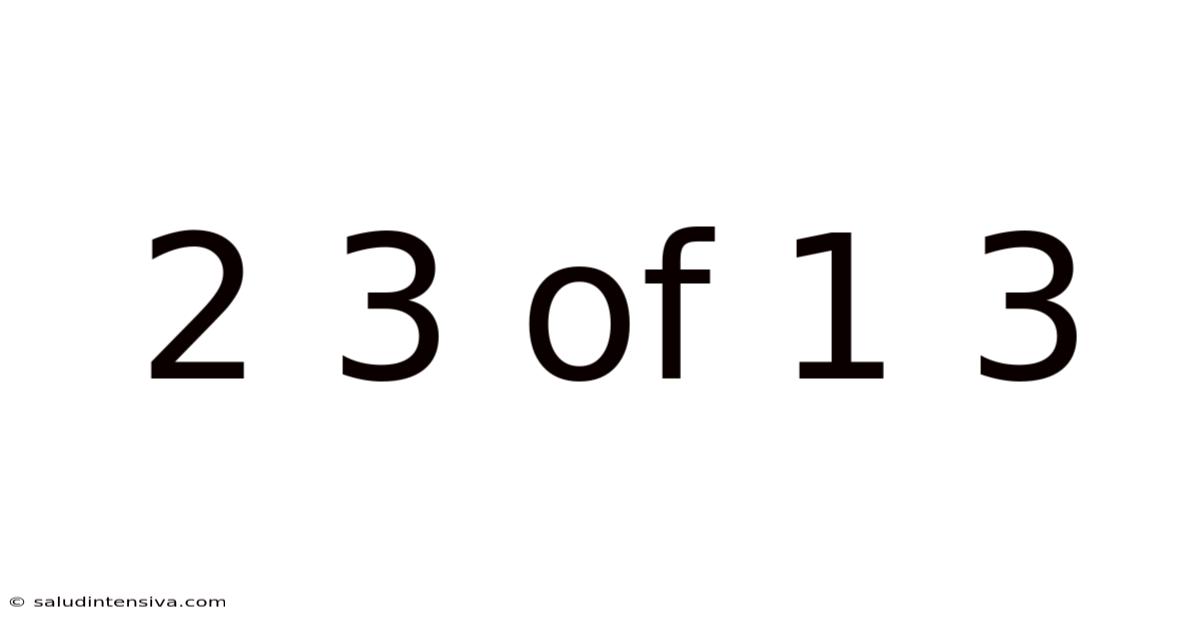
Table of Contents
Understanding the Fraction 2/3 of 1/3: A Comprehensive Guide
This article will delve into the seemingly simple yet often misunderstood concept of finding a fraction of a fraction, specifically calculating 2/3 of 1/3. We'll break down the process step-by-step, explore the underlying mathematical principles, and answer frequently asked questions to ensure a comprehensive understanding. This guide is perfect for anyone looking to solidify their grasp of fractions, from elementary school students to adults brushing up on their math skills. Mastering this concept is crucial for various mathematical applications, building a strong foundation for more advanced topics.
Understanding Fractions: A Quick Recap
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/3, the numerator is 1, and the denominator is 3. This means we have 1 part out of a total of 3 equal parts.
Calculating 2/3 of 1/3: A Step-by-Step Approach
The phrase "of" in mathematics often signifies multiplication. Therefore, calculating 2/3 of 1/3 is equivalent to multiplying the two fractions: (2/3) x (1/3). Here's how to perform this calculation:
Step 1: Multiply the Numerators:
Multiply the numerators together: 2 x 1 = 2
Step 2: Multiply the Denominators:
Multiply the denominators together: 3 x 3 = 9
Step 3: Combine the Results:
Combine the results from Step 1 and Step 2 to form the final fraction: 2/9
Therefore, 2/3 of 1/3 is 2/9.
Visualizing the Calculation
Visualizing the calculation can make it easier to grasp. Imagine a rectangle divided into three equal parts. Each part represents 1/3. Now, let's consider 2/3 of this rectangle. This would mean taking two out of the three equal parts. Each of these two parts is still further divided into three equal parts. Therefore, by taking 2/3 of 1/3, we end up with 2 out of 9 equal parts of the original rectangle. This visually confirms that 2/3 of 1/3 equals 2/9.
The Mathematical Principle Behind Fraction Multiplication
The process of multiplying fractions involves multiplying the numerators and then multiplying the denominators. This principle stems from the fundamental concept of fractions as representing parts of a whole. When we multiply fractions, we are essentially finding a fraction of a fraction, representing a smaller part of an already divided whole. The multiplication of the numerators reflects the combined number of parts we select, and the multiplication of the denominators reflects the total number of equal parts in the whole.
Extending the Concept: Calculating Fractions of Fractions in General
The method used to calculate 2/3 of 1/3 applies to any fraction multiplication. To find a fraction of another fraction, always follow these steps:
- Multiply the numerators.
- Multiply the denominators.
- Simplify the resulting fraction (if possible).
For example:
- (1/4) x (2/5) = (1 x 2) / (4 x 5) = 2/20 = 1/10
- (3/7) x (4/9) = (3 x 4) / (7 x 9) = 12/63 = 4/21 (simplified by dividing both numerator and denominator by 3)
Dealing with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To multiply fractions involving mixed numbers, first convert the mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
For example, to calculate (1 1/2) x (2/3):
-
Convert 1 1/2 to an improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
-
Multiply the improper fraction by the other fraction: (3/2) x (2/3) = (3 x 2) / (2 x 3) = 6/6 = 1
Therefore, (1 1/2) x (2/3) = 1
Simplifying Fractions: A Crucial Step
After multiplying fractions, always simplify the resulting fraction to its lowest terms. This means reducing the numerator and denominator by dividing both by their greatest common divisor (GCD). For example, the fraction 12/18 can be simplified to 2/3 by dividing both the numerator and denominator by 6 (the GCD of 12 and 18).
Frequently Asked Questions (FAQ)
Q: Why do we multiply the numerators and denominators separately?
A: This stems from the definition of a fraction and the concept of multiplication. We're essentially finding a fraction of a fraction, representing a smaller part of an already divided whole. Multiplying the numerators reflects the combined parts selected, while multiplying the denominators reflects the total parts of the new whole.
Q: What if I get a fraction with a large numerator and denominator?
A: Simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This makes the fraction easier to understand and use.
Q: Can I use a calculator to multiply fractions?
A: Yes, most calculators can handle fraction multiplication. However, understanding the underlying process is essential for building a strong mathematical foundation.
Q: How does this relate to real-world problems?
A: Understanding fractions and fraction multiplication is essential for many real-world applications, including cooking, construction, sewing, and various aspects of engineering and science.
Conclusion: Mastering Fractions for a Brighter Future
Understanding how to calculate fractions of fractions, like 2/3 of 1/3, is a fundamental skill with wide-ranging applications. By mastering this concept, you build a stronger foundation in mathematics, opening doors to more advanced topics and enabling you to tackle real-world problems with confidence. Remember the key steps: multiply the numerators, multiply the denominators, and simplify the resulting fraction. Practice regularly, and you'll soon find yourself effortlessly navigating the world of fractions. This skill isn't just about passing a math test; it's about developing a crucial life skill applicable in countless situations. So, embrace the challenge, and enjoy the rewarding journey of mastering fractions!
Latest Posts
Latest Posts
-
How Long Is 204 Minutes
Sep 13, 2025
-
Gcf Of 10 And 14
Sep 13, 2025
-
11 50 As A Decimal
Sep 13, 2025
-
How To Rewrite Improper Fractions
Sep 13, 2025
-
6am 2pm Is How Many Hours
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Of 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.