2 3 Plus 1 6
saludintensiva
Sep 17, 2025 · 6 min read
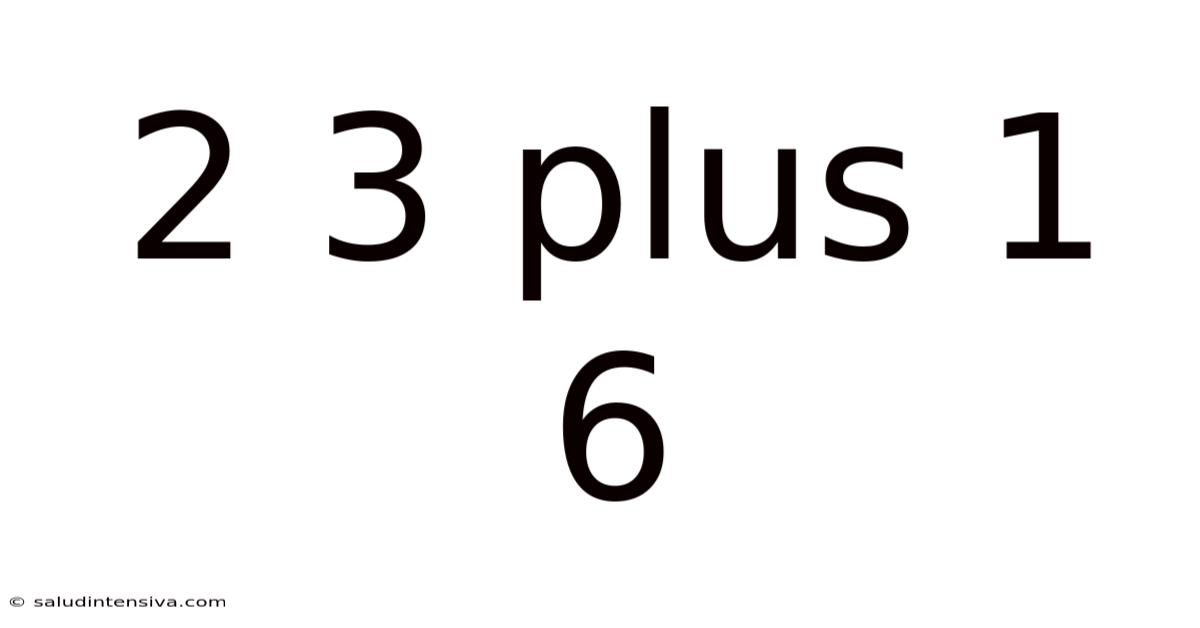
Table of Contents
Decoding the Enigma: A Deep Dive into "2 3 Plus 1 6"
This article delves into the seemingly simple mathematical expression "2 3 plus 1 6," exploring its various interpretations, the underlying mathematical principles, and the broader implications of understanding number relationships. While the initial presentation might appear straightforward, we'll uncover layers of complexity and potential ambiguity, highlighting the importance of precise mathematical notation and the power of different mathematical frameworks. The exploration will cover basic arithmetic, order of operations, potential interpretations as vector addition, and even touch upon the philosophical implications of representing information.
Understanding the Initial Ambiguity: Interpretation Matters
At first glance, "2 3 plus 1 6" might seem like a straightforward addition problem. However, the lack of standardized mathematical notation introduces ambiguity. Does "2 3" represent the number twenty-three, or does it imply a different operation, perhaps multiplication or concatenation? Similarly, "1 6" could be interpreted as sixteen, or represent a separate entity altogether. This ambiguity is precisely what makes this seemingly simple expression an excellent case study in clarifying mathematical communication. The core issue lies in the critical need for clear and unambiguous notation in mathematics. Without it, even the simplest expressions can lead to multiple interpretations and potentially incorrect results.
Basic Arithmetic Interpretation: The Most Likely Scenario
Assuming the most straightforward interpretation, "2 3 plus 1 6" translates to 23 + 16. In this scenario, the numbers are treated as base-10 integers, and the "+" symbol denotes standard addition. Therefore, the solution is simple:
23 + 16 = 39
This is the most likely interpretation given the general context of numerical expressions. However, it is crucial to acknowledge the potential for other interpretations, especially in more advanced mathematical contexts.
Exploring Alternative Interpretations: Beyond Basic Arithmetic
While the basic arithmetic interpretation is straightforward, let's consider alternative perspectives that highlight the power of different mathematical systems.
1. Concatenation and Addition:
We could interpret "2 3" as the concatenation of the digits 2 and 3, resulting in the number 23. Similarly, "1 6" would be 16. However, the word "plus" still suggests addition. Therefore, the calculation would still result in:
23 + 16 = 39
2. Vector Addition:
In linear algebra, numbers can be represented as vectors. If we consider "2 3" as a vector (2, 3) and "1 6" as a vector (1, 6), the "plus" symbol could represent vector addition. Vector addition is performed component-wise. Therefore:
(2, 3) + (1, 6) = (2+1, 3+6) = (3, 9)
This demonstrates that the interpretation of "plus" changes the result dramatically, depending on the mathematical context.
3. Base Systems:
The interpretation could also change if we considered different base systems. While base 10 is the most common, other systems exist. For instance, if we were working in a base-16 (hexadecimal) system, "2 3" and "1 6" would have different numerical values. However, without explicit mention of a different base, assuming base-10 is generally accepted.
The Importance of Mathematical Notation: A Lesson in Precision
The ambiguity surrounding "2 3 plus 1 6" underscores the critical importance of precise mathematical notation. Ambiguous expressions can lead to errors and misinterpretations. Established mathematical notation provides clarity and ensures consistent results regardless of the interpreter. Formal mathematical notation, such as using parentheses, clearly defined operators, and explicit base specification, is vital for avoiding confusion and ensuring accuracy. In this particular case, writing the expression as "(23) + (16)" eliminates any ambiguity regarding the intended operation.
Expanding on the Concepts: Related Mathematical Ideas
Let's expand our understanding by touching upon some related mathematical concepts that are interconnected with the "2 3 plus 1 6" problem.
1. Order of Operations (PEMDAS/BODMAS):
While this particular problem doesn't involve multiple operations requiring the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), it’s crucial to understand this fundamental principle in mathematics. PEMDAS/BODMAS dictates the sequence in which operations should be performed within a complex mathematical expression. Mastering this ensures consistent results when dealing with more intricate expressions.
2. Number Systems:
Our exploration briefly touched upon different base systems. Understanding different number systems (binary, octal, decimal, hexadecimal, etc.) expands our perspective on representing numerical data. This knowledge is essential in various fields like computer science and cryptography.
3. Set Theory:
While not directly applicable here, set theory provides a framework for understanding collections of objects. In a broader sense, the numbers 2, 3, 1, and 6 could be considered elements of a set, and operations on sets (union, intersection, etc.) could be introduced, though not directly relevant to the simple addition problem presented.
4. Abstract Algebra:
This branch of mathematics deals with abstract structures and their properties. Although our simple expression doesn't readily lend itself to abstract algebraic analysis, it provides a fundamental introduction to how numbers and operations can be generalized and studied within abstract frameworks.
Frequently Asked Questions (FAQ)
Q: What is the most common interpretation of "2 3 plus 1 6"?
A: The most common and logical interpretation is 23 + 16 = 39, treating "2 3" and "1 6" as the numbers twenty-three and sixteen, respectively.
Q: Can "2 3" represent something other than the number twenty-three?
A: Yes, depending on the context, "2 3" could represent concatenation (2 followed by 3), a coordinate in a two-dimensional space, or even something entirely different within a specialized mathematical system. This is why clear notation is essential.
Q: What is the importance of precise mathematical notation?
A: Precise notation is crucial for avoiding ambiguity and ensuring that the intended calculation or meaning is clearly understood. It guarantees consistent results and prevents misinterpretations.
Q: Are there any other mathematical concepts related to this simple expression?
A: Yes, concepts like order of operations (PEMDAS/BODMAS), different number systems, set theory, and abstract algebra are related, highlighting the interconnectedness of mathematical ideas.
Conclusion: The Power of Clear Communication
The seemingly simple expression "2 3 plus 1 6" serves as a powerful reminder of the importance of clear and unambiguous mathematical notation. While the most likely interpretation leads to the straightforward answer of 39, exploring alternative interpretations highlights the richness and flexibility of mathematics. This exploration not only provides a solution to a simple arithmetic problem but also introduces fundamental mathematical concepts and emphasizes the necessity of precise communication in mathematics, a critical element in ensuring accuracy and avoiding confusion in any field that utilizes mathematical principles. The underlying message is that even simple expressions can harbor complexities when the context and notation are not clearly defined. Therefore, striving for clear communication is paramount in mathematics and all aspects of scientific and technical endeavors.
Latest Posts
Latest Posts
-
Double Declining Balance Method Example
Sep 17, 2025
-
8 Ft Divided By 3
Sep 17, 2025
-
Greatest Common Factor Of 90
Sep 17, 2025
-
15 16 As A Percentage
Sep 17, 2025
-
Are 3 4 And 6 8 Equivalent
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Plus 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.